K近邻算法——KNN

KNN（K-Nearest Neighbor）算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。所以比较特殊的是它不需要训练，易于理解，易于实现。

在KNN中，通过计算对象间距离来作为各个对象之间的相似性指标，在这里距离一般使用欧氏距离或曼哈顿距离：

 

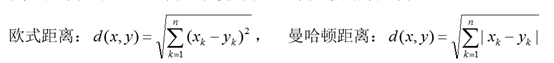
整个KNN算法过程可以描述为：输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，其算法的描述为：

计算测试数据与各个训练数据之间的距离；

按照距离的递增关系进行排序；

选取距离最小的K个点；

确定前K个点所在类别的出现频率；

返回前K个点中出现频率最高的类别作为测试数据的预测分类。

 

从KNN算法思想上思考，该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。该算法只计算"最近的"邻居样本，某一类的样本数量很大，那么或者这类样本并不接近目标样本，或者这类样本很靠近目标样本。无论怎样，数量并不能影响运行结果。但是本实验有个缺陷是有个别类别的文本很少。所以有这样一个缺点。另一个不足之处是计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。