1.5 因果律
写在前面的废话
在本章中,我们会讨论一下因果关系,我们知道事件发生往往是先发生“因”,后发生“果”,但是相对论似乎给我们了一个因果倒置的可能性。本章中我们会探讨一下因和果之间的关系,并体积一些你们当中相当感兴趣的时间反演(时间倒流)的问题
例题一
长\(100m\)的车厢,以\(u=0.6c\)的速度驶过站台。有两人A和B分别站在车厢尾部和头部,各执一把手枪。两人开枪,站台上的人观测到A比B先开抢\(0.125μs\)。问车厢上的乘客看来,谁先开枪?并求出开枪间隔。
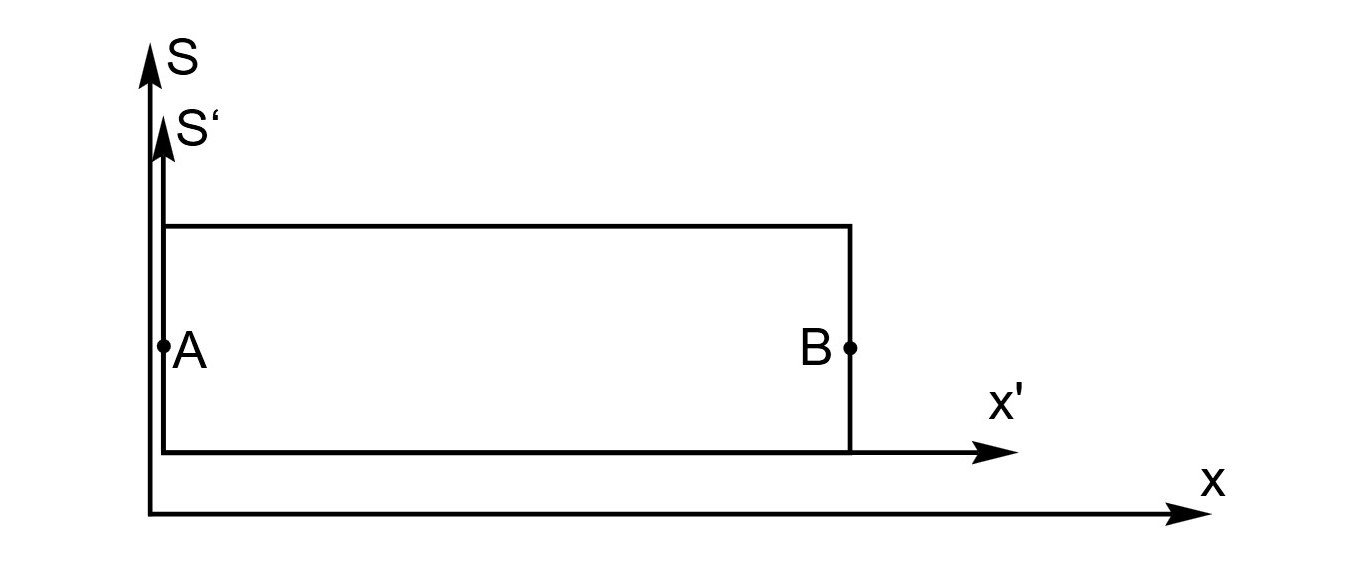
分析:
设地面为\(S系\),车厢为\(S'系\)
设当A开枪时,
\(S系\)中\(x_A=0\) \(t_A=0\)
\(S'系\)中\(x_A'=0\) \(t_A'=0\)
设当B开枪时,
\(S系\)中\(x_A=0\) \(t_A=0\)
\(S'系\)中\(x_A'=0\) \(t_A'=0\)
整理一下得到这样的一张表:
| \(S系(地面)\) | \(S'系(车厢)\) | |
|---|---|---|
| A开枪 | \(x_A=0 t_A=0\) | \(x_A'=0 t_A'=0\) |
| B开枪 | \(x_B t_B=0.125×10^{-6}s\) | \(x_B'=100 t_B'\) |
| \(u=0.6c γ=\frac{1}{0.8}\) | ||
| \(t_B=(t_B'+\frac{ux_B'}{c^2})·\frac{1}{0.8}\) | ||
| \(⇒0.125×10^{-6}=(t_B'+\frac{0.6c×100}{c^2})·\frac{1}{0.8}\) | ||
| \(⇒t_B'=-0.1×10^{-6}s=-0.1μs\) | ||
| 故乘客观测到B先于A 0.1μs开枪 | ||
| 这就很有意思了,车外的人看到A先开枪,而车上的人看到B先开枪,那么如果A与B开枪的两个事件有因果关系,如A开枪B倒下,那车外的人将会看到怎样的景象? | ||
| 那我们再讨论一下: | ||
| 若在\(S系\)中,A、B两事件有因果关系(\(t_B>t_A\))又能得到这样一张表: | ||
| \(S系\) | \(S'系\) | |
| :----: | :----: | :----: |
| A事件 | \(x_A t_A\) | \(x_A' t_A'\) |
| B事件 | \(x_B t_B\) | \(x_B' t_B'\) |
| 在\(S'系\)中,将有: | ||
| \(t_A'=(t_A-\frac{u_{x_A}}{c^2})·γ\) | ||
| \(t_B'=(t_B-\frac{u_{x_B}}{c^2})·γ\) | ||
| 在\(S'\)系中: | ||
| \(Δt'=t_B'-t_A'=[(t_B-t_A)\frac{u(x_B-x_A)}{c^2}]·γ\) | ||
| 那么只要这坨\(t_A-t_B<[(t_B-t_A)\frac{u(x_B-x_A)}{c^2}]\) | ||
| 那么\(Δt'<0\)因果就倒置了。 | ||
| 看到这里,想必一些 |
||
| 但 | ||
| 肯定没那么简单,不然这种方法早就公诸于世了 | ||
| 那具体是怎么一回事呢? | ||
| 我们设信号速度\(v=\frac{x_B-x_A}{t_B-t_A}\) | ||
| 则:\(t_A-t_B<\frac{u}{c^2}(x_B-x_A)\) | ||
| \(⇒\frac{u}{c^2}·\frac{x_B-x_A}{t_B-t_A}>1\) | ||
| \(⇒\frac{u·v}{c^2}>1\) | ||
| 只要\(u>c\)或\(v>c\)就能实现时间倒流了!是不是感觉很激动?!但是仔细一想,发现两个条件都不能实现。 | ||
| 所以还是必然是前因后果,保证因果律的绝对性。 |
但是为什么前面一个例题中发生了因果倒置呢?
当然是因为两件事情没有因果关系啊。
讲完了这些,我们再来做几道与因果律关系不大的练习夯实你的学习成果吧。
练习
地面上D点有一个发射台,其东、西两侧\(l_0=10^3cm\)处有两个接收站E、W,,飞船以WE连线以\(u=0.6c\)飞行,此时,D点发出一个电磁脉冲,求飞船上的人观测到E、W两点接收到信号的时间间隔。
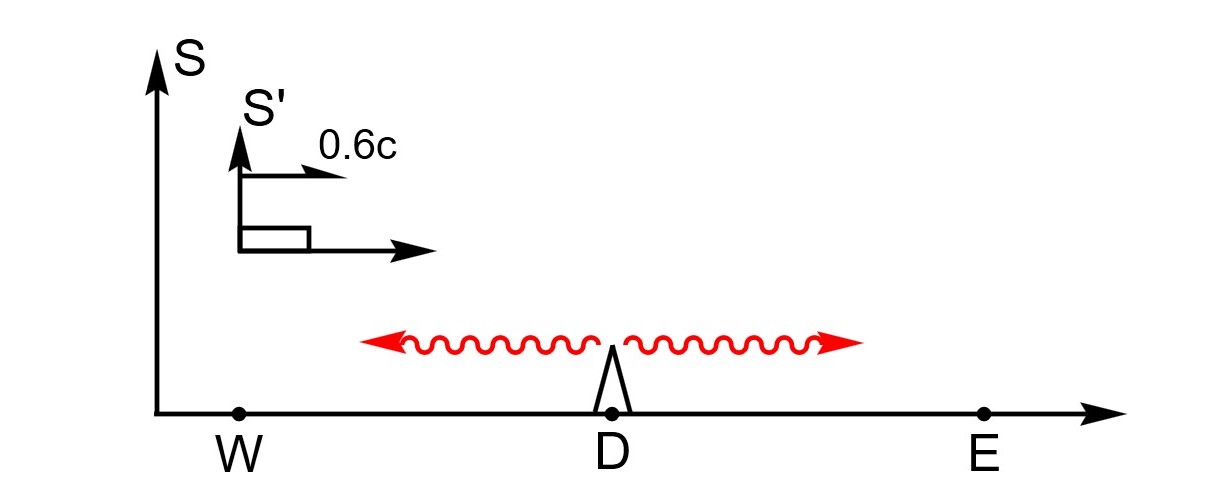
解:\(u=0.6c γ=\frac{1}{0.8}\)
在\(S系\)中,\(Δt=0\)
在\(S'系\)中,
\(t_E'=(t_E-\frac{u·x_E}{c^2})·γ\)
\(t_W'=(t_W-\frac{u·x_W}{c^2})·γ\)
\(Δt'=t_W'-t_E'\)
\(=[(t_W-t_E)+\frac{u(x_E-x_W)}{c^2}]·γ\)
\(=(0+\frac{u·2l_0}{c^2})·γ\)
\(=5×10^{-3}s\)
\(=5ms(毫秒)\)
∴ 先到E,后到W

