1.3.1 洛伦兹因子与爱因斯坦延缓（钟慢效应）

写在前面的一些废话

介于担心有人看到标题就不想点开看了，这一章原来题目叫做钟慢效应。但是我的一个精神方面的赞助商建议我写成爱因斯坦延缓，于是我照做了。爱因斯坦延缓本意就是越快的物体时间流逝速度越慢，相信大家都应该有所耳闻。本章节有亿些的计算和练习题，没有兴趣的同学可以直接跳过练习部分（关于爱因斯坦延缓的理论部分还是有必要看看的，可以说这是狭义相对论中最重要的内容了）。

爱因斯坦延缓

情景

爱因斯坦车厢，高\(h\)，沿\(x轴\)正方向高速运动，有一光脉冲从车厢底部发出，在车厢顶部反射回车厢底部。

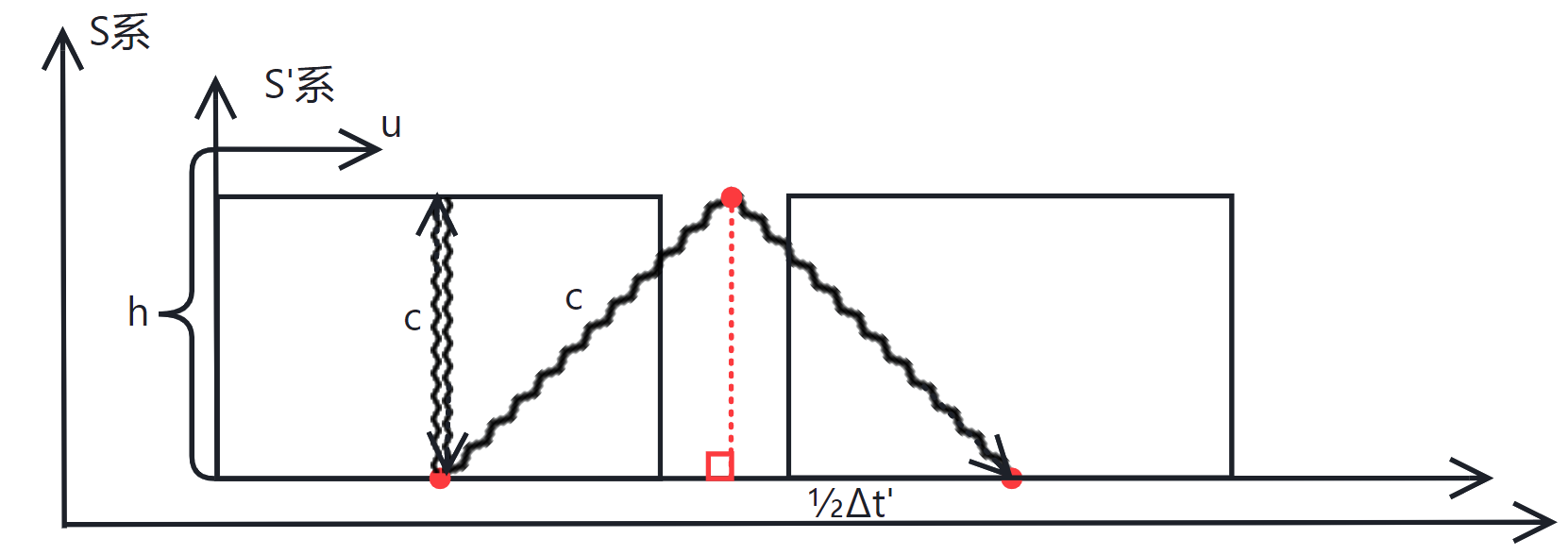
\(S'系\)中，光脉冲上下往返所需时间间隔为\(Δt=\frac{2h}{c}\)
\(S系\)中，使用速度乘以时间计算出光脉冲走过的路程为\(s=\frac{1}{2}Δt'·c\)
使用勾股定理计算出光脉冲走过的路程为\(s'=\sqrt{(\frac{1}{2}Δt·c)^2+(\frac{1}{2}Δt'·u)^2}\)
由于光在同一个参考系内运动路程相同，即\(s=s'\)
⇒\(\frac{1}{2}Δt'·c=\sqrt{(\frac{1}{2}Δt·c)^2+(\frac{1}{2}Δt'·u)^2}\)
⇒\(Δt'=\frac{2h}{c\sqrt{1-\frac{u^2}{c^2}}}=\frac{Δt}{\sqrt{1-\frac{u^2}{c^2}}}\)
因为任何物体运动速度都无法超越光速，所以\(u<c\)
⇒\(\sqrt{1-\frac{u^2}{c^2}}<1\)
⇒\(Δt'>Δt\)
从这个式子中我们可以发现在\(S'系\)中，时间流逝比\(S系\)慢，即运动的时钟会走得慢，又称钟慢效应
我们令\(\frac{1}{\sqrt{1-\frac{u^2}{c^2}}}=γ\)，又称洛伦兹因子
因为\(\sqrt{1-\frac{u^2}{c^2}}<1\)即\(\frac{1}{γ}<1\)
所以\(γ>1\)
\(Δt'=γ·Δt\)
p.s. \(γ\)（洛伦兹因子）这个东西还是十分有用的，以后几章里会比较详细地讲解\(γ\)的具体用途和意义
\(Δt\)为某参考系中同一地点两事件的时间间隔，称为本征时间，有教材称原时间或固有时间（我个人还是比较喜欢称作本征时间）

例一：μ子的子生巅峰

宇宙射线进入大气层，与大气分子碰撞，产生\(μ\)子，\(μ\)子产生后高速向地球移动，速度\(u=0.998c\)，\(μ\)子静止时寿命约为\(2.15×10^{-6}\)，试问为何\(μ\)子能穿过\(9km\)的大气，使我们能在地面上观测到？
分析：
按照经典物理：\(d=ut=0.998×(3×10^8)×2.15×10^{-6}=643.71m\)
这样算下来这颗可怜的\(μ\)子飞了不到\(700m\)就湮灭没了。
这当然不对了。这速度\(0.998c\)，一看就知道经典物理肯定要有“误差”，那就用相对论物理试试。
考虑钟慢效应：
在\(μ\)子参考系中：\(Δt_0=2.15×10^{-6}\)
在地面参考系中：\(Δt'=γ·Δt_0=\frac{Δt_0}{\sqrt{\frac{u^2}{c^2}}}=\frac{2.15×10^{-6}}{\sqrt{1-\frac{u^2}{c^2}}}≈3.4×10^{-6}\)
\(d=u·Δt_0=0.998×(3×10^8)×3.4×10^{-5}=10179.6m\)
这下就对了嘛，\(μ\)子在它生命的开始也是最后的\(2.15×10^{-6}s\)内还有机会从大气层出发，来到地球表面，达到子生巅峰！多么励志的故事啊！一定要用来教育小朋友

例二：如何正确缩短跑一千米的时间

由上文可知，运动的钟走的越慢，那运动的我们手上的表肯定也越慢啦。一千米的成绩应该以我们手上的表为准才对（毕竟要以学生的参照系为准嘛）。下面的这个情景就能让你深刻体会到你的表慢了多少。
首先说明一点，我不是什么军事迷，但是也略懂一些

情景

SR-71黑鸟战斗机，假设一直以速度\(u=900m/s\)做匀速直线运动，以地面为参考系。求飞机飞行多久飞机上飞行员的手表会比地面上的钟慢一秒？（假设在理想环境中，不计油耗，且飞行员携带的手表和地面上的钟都绝对准确）
解：设飞行员参考系经过的时间为\(Δt_0\)，
地面参考系经过的时间为\(Δt\)
\(Δt=γ·Δt_0\)
\(Δt-Δt_0=1\)
\(⇒Δt=γ·(Δt-1)\)
\(⇒Δt=\frac{1}{γ-1}≈2.22×10^{11}≈7046年\)
嗯，不错不错，也就七千多年嘛（假设有一群人，个个都能活到100岁，他们一个死了另一个紧接着出生，也就70个人就能解决了）。
那回到我们最开始的问题，跑步也是这样吗？废话。我们还是看一下那个洛仑兹因子\(γ=\frac{1}{\sqrt{1-\frac{u^2}{c^2}}}\)，本身人跑的速度相对于光速就很小了，再开个平方，这数字不用四舍五入直接约等于0啊，用1减去它，再开个根，取个倒数，约等于1……
总之\(γ=1\)就完事了，得出\(Δt=Δt_0\)。
当然，秉持着科学的研究态度，我们还是算一下你手上的表会慢多少吧。
首先估测一下跑步速度，我作为我们班一千米第一名常年稳定在三分半左右（第二名差不多稳定在四分钟）。
就算是四分半吧，\(v=\frac{s}{t}=\frac{1000m}{270s}≈4m/s\)（四舍五入一下好算点）
\(γ=\frac{1}{\sqrt{1-\frac{u^2}{c^2}}}\)
\(=\frac{1}{\sqrt{1-\frac{4^2}{c^2}}}\)
由于普通计算器精度不高，于是我就用Google Chrome的Console计算。虽然精度也不高

不多不多！多乎哉？不多也。

结论

所以说，用相对论解低速问题好像并没有什么意义，就没有必要和体育老师争这么五十亿亿分之一秒了吧。以后和同学装B的时候挑一些大点的数据算（记得别超过光速\(3×10^8m/s\)！）。

例三：参考系

在某参考系中，两事件同地发生，该参考系中时钟测得两事件发生时间间隔为4s。另一参照系中，测得这两个事件时间间隔为5s，求这两个参照系的相对速度。
解：\(Δt\)为本征时间
\(Δt=γ·Δt_0\)
\(γ=\frac{Δt}{Δt_0}=\frac{5}{4}\)
\(\frac{1}{\sqrt{1-\frac{u^2}{c^2}}}=\frac{5}{4}\)
\(⇒u=0.6c\)

例四：飞船

飞船以速度\(u=0.8c\)离开地球，并先后发出两个光信号，地球观测者接收到两个信号的时间间隔为\(12s\)。问飞船上宇航员发出这两个光信号的时间间隔为多少？

解：
取地球\(S系\)，飞船\(S'系\)
飞船上测得本征时间\(Δt_0\)
在\(S系\)中，两事件时间间隔\(Δt=γ·Δt_0\)
考虑到飞船远离地球，在\(Δt\)的时间内，飞船飞行\(u·Δt\)，即\(\frac{u·Δt}{c}\)为光信号传播的时间。
\(12=Δt+\frac{u·Δt}{c}\)
\(⇒12=γ·Δt_0+\frac{u}{c}·γ·Δt_0\)
\(⇒Δt_0=\frac{12}{(1+\frac{u}{c})·γ}=\frac{12}{(1+\frac{u 0.8c}{c})·\frac{1}{0.6}}=4s\)