受限玻尔兹曼机(Restricted Boltzmann Machine)分析
1、什么是BM?
BM是由Hinton和Sejnowski提出的一种随机递归神经网络,可以看做是一种随机生成的Hopfield网络,是能够通过学习数据的固有内在表示解决困难学习问题的最早的人工神经网络之一,因样本分布遵循玻尔兹曼分布而命名为BM。BM由二值神经元构成,每个神经元只取1或0这两种状态,状态1代表该神经元处于接通状态,状态0代表该神经元处于断开状态。在下面的讨论中单元和节点的意思相同,均表示神经元。
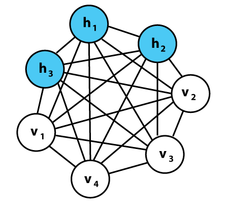
上图为一个玻尔兹曼机(BM),其蓝色节点为隐层,白色节点为输入层。
玻尔兹曼机和递归神经网络相比,区别体现在以下几点:
1、递归神经网络(RNN)本质是学习一个映射关系,因此有输入和输出层的概念,而玻尔兹曼机的用处在于学习一组数据的“内在表示”,因此其没有输出层的概念。
2、递归神经网络各节点链接为有向环,而玻尔兹曼机各节点连接成无向完全图。
2、什么是RBM?
限制玻尔兹曼机中,所谓的限制就是:将完全图变成了二分图。如图所示,限制玻尔兹曼机由三个显层节点和四个隐层节点组成。

RBM中,所有可见单元和隐单元之间存在连接,而隐单元两两之间和可见单元两两之间不存在连接,也就是层间全连接,层内无连接(这也是和玻尔兹曼机BM模型的区别,BM是层间、层内全连接)。其中,每一个节点(无论是Hidden Unit还是Visible Unit)都有两种状态:处于激活状态时值为1,未被激活状态值为0。
这里的0和1状态的意义是代表了模型会选取哪些节点来使用,处于激活状态的节点被使用,未处于激活状态的节点未被使用。节点的激活概率由可见层和隐藏层节点的分布函数计算。
RBM本质是非监督学习(Unsupervised Learning)的利器(Hinton和吴恩达都认为:将来的机器学习任务慢慢都会转变为非监督学习的),因为,它可以用于降维(隐层少一点),学习特征(隐层输出就是特征),自编码器(AutoEncoder)以及深度信念网络(多个RBM堆叠而成)等。
3、RBM
一个RBM中,v表示所有可见层单元,h表示所有隐层单元。要想确定该模型,只要能够得到模型三个参数:W、A和 B。分别是权重矩阵W,可见层单元偏置A,隐藏层单元偏置B。假设一个RBM有n个可见单元和m个隐单元,用vi表示第i个可见单元,hj表示第j个隐单元,它的参数形式为:
Wij: 表示第i个可见单元和第j个隐单元之间的权值。
ai: 表示第i个可见单元的偏置阈值。
bj: 表示第j个隐单元的偏置阈值。
对于一组给定状态下的(v, h)值,假设可见层单元和隐藏层单元均服从伯努利分布,RBM的能量公式是:
\(E(v,h|\theta) = -\sum_{i=1}^n a_iv_i - \sum_{j=1}^m b_jh_j - \sum_{i=1}^n\sum_{j=1}^m v_iW_{ij}h_j\)
其中\(\theta = {W_{ij}, a_i, b_j}\)
为RBM模型的参数,能量函数表示在每一个可见节点和每一个隐藏层节点之间都存在一个能量值。
对该能量函数指数化和正则化后可以得到可见层节点集合和隐藏层节点集合分别处于某一种状态下(v, h)联合概率分布公式:
\(P(v,h|\theta) = \frac {e^{-E(v,h|\theta)}} {Z(\theta)}\)
\(Z(\theta) = \sum_{v,h} e^{-E(v,h|\theta)}\)
其中,Z(θ)为归一化因子或配分函数(partition function),表示对可见层和隐藏层节点集合的所有可能状态的(能量的指数形式)求和。
对于参数的求解往往采用似然函数求导的方法。已知联合概率分布P(v,h|θ),通过对隐藏层节点集合的所有状态求和,可以得到可见层节点集合的边缘分布P(v|θ):
\(P(v|\theta) = \frac {1} {Z(\theta)} \sum_{h}e^{-E(v,h|\theta)}\)
边缘分布表示的是可见层节点集合处于某一种状态分布下的概率,边缘分布往往被称为似然函数(如何对模型参数求解在下面章节阐述)。
由于RBM模型的结构(层间全连接、层内无连接),它具有以下重要性质:
1)在给定可见单元的状态时,各隐藏层单元的激活状态之间是条件独立的。此时,第j个隐单元的激活概率为:
\(P(h_j=1|v) = f(b_j+\sum_i v_iW_{ij})\)
2)相应的,当给定隐单元的状态时,可见单元的激活概率同样是条件独立的:
\(P(v_i=1|h) = f(a_i+\sum_j W_{ij}h_j)\)
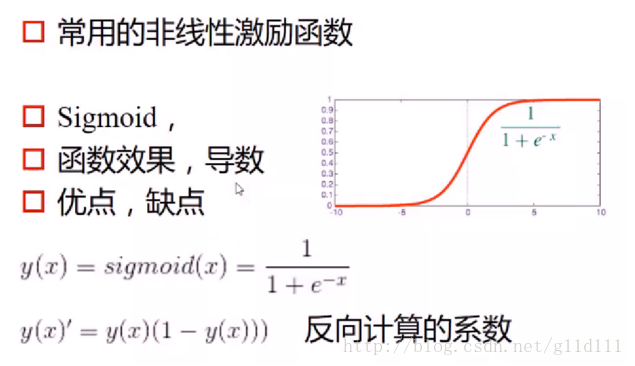
f 为激励函数/激活函数,这里选用sigmoid作为激活函数。是因为它可以把(-∞,+∞)的值映射到[0,1]这个区间。也就是说,无论模型的可见层输入节点数据处于一个多大的范围内,都可以通过sigmoid函数求得它相应的函数值,即节点的激活概率值。
4、RBM模型参数求解
在给定一个训练样本后,训练一个RBM的意义在于调整模型的参数,以拟合给定的训练样本,使得在该参数下RBM表示的可见层节点概率分布尽可能的与训练数据相符合。
对于该模型需要确定两部分。一是如果想确定这个模型,首先是要知道可见层和隐藏层节点个数,可见层节点个数即为输入的数据维数,隐藏层节点个数在一些研究领域中是和可见层节点个数有关的,如用卷积受限玻尔兹曼机处理图像数据,在这里不多分析。
但多数情况下,隐藏层节点个数需要根据使用而定或者是在参数一定的情况下,使得模型能量最小时的隐藏层节点个数。
其次,要想确定这个模型还得要知道模型的三个参数\(\theta = {W_{ij}, a_i, b_j}\),下面就围绕着参数的求解进行分析。
由上文提到,参数求解用到了似然函数的对数对参数求导。
\(P(v|\theta) = \frac {1} {Z(\theta)} \sum_{h}e^{-E(v,h|\theta)}\)
可知,能量E和概率P是成反比的关系,所以通过最大化P,才能使能量值E最小。最大化似然函数常用的方法是梯度下降法(这是NN主流方法,在此不再赘述。)
对数似然函数对参数求导分析:
首先是似然函数的对数形式:ln(P(v^{t})), vt表示模型的输入数据。
然后对参数W_{ij}, a_i, b_j分别进行求导,以W_{ij}为例:
\(\frac {\partial ln(P(v^{t}))} {\partial w_{ij}} = P(h_j=1|v_t)v_i^t - \sum_v P(v)P(h_j=1|v)v_i\)
\(\frac {\partial ln(P(v^{t}))} {\partial a_i} = v_i^t - \sum_v P(v)v_i\)
\(\frac {\partial ln(P(v^{t}))} {\partial b_j} = P(h_j=1|v_t) - \sum_v P(v)P(h_j=1|v)\)
由于上面三式的第二项中都含有P(v), P(v)中仍然含有参数,所以它是式中求不出来的。所以,有很多人就提出了一些通过采样逼近的方法来求每一个式子中的第二项。
5、Gibbs采样算法
因为在上一节末尾讲对参数的求导中仍然存在不可求项P(v), P(v)表示可见层节点的联合概率。所以,要想得到P(v)的值,就得要逼近它,求它的近似值。
Gibbs采样的思想是:虽然不知道一个样本数据\(x = (x_1, x_2, ... , x_n)\)的联合概率P(x),但是知道样本中每一个数据的条件概率\(P(x_i|x_1,x_2,...,x_{i-1},x_{i+1},...,x_n)\)(假设每一个变量都服从一种概率分布),则我可以先求出每一个数据的条件概率值,得到x的任一状态[\(x_1(0), x_2(0), ..., x_n(0)]\)。然后,我用条件概率公式迭代对每一个数据求条件概率。最终,迭代k次的时候,x的某一状态\([x_1(k), x_2(k), ..., x_n(k)]\)将收敛于x的联合概率分布P(x) 。
对于RBM来讲,则执行过程如下图所示:
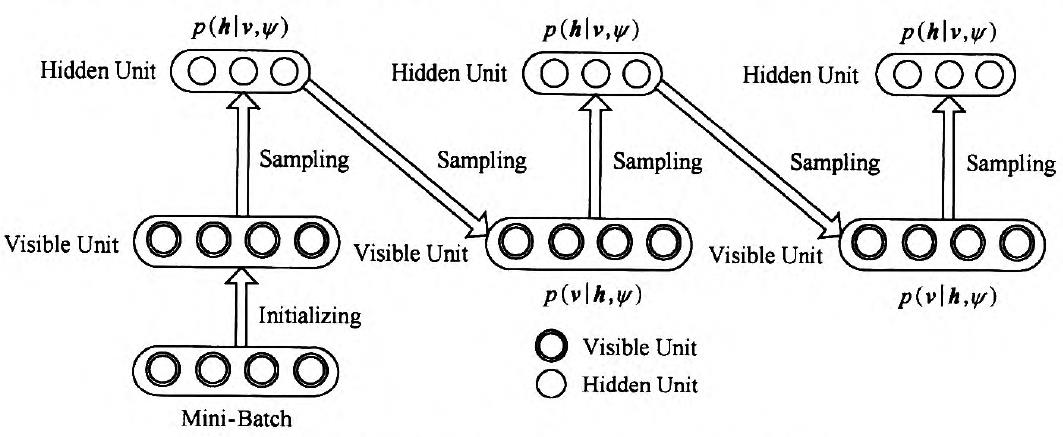
Gibbs采样过程
求解过程是:
假设给我一个训练样本v0,根据公式 :
\(P(h_j=1|v_0) = f(b_j+\sum_{i \in v_0} v_iW_{ij})\)
求 h0中每个节点的条件概率;
再根据公式
\(P(v_i=1|h_0) = f(a_i+\sum_{j \in h_0}W_{ij}h_j)\)
求v1中每个节点的条件概率,然后依次迭代,直到执行K步(K足够大),此时P(v|h)的概率将收敛于P(v)的概率。如下所示:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号