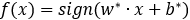支持向量机(三)-线性支持向量机与软间隔最大化
1.线性可分支持向量机的局限性
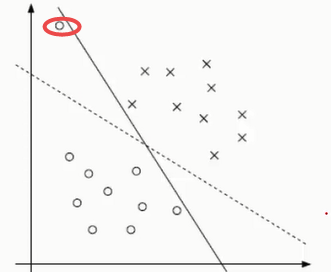
在支持向量机(二)中我们已经推导了线性可分支持向量机的原理,但在实际问题中,我们的样本数据可能并不那么完美,可能含有一些噪音点或者异常点,如果我们不考虑噪音点依然使用之前的线性可分模型去考量,那找到的分离超平面未必是最合适的,如下图所示,红圈所示圆点很明显是一个噪音点,此时用线性可分的原理去寻找超平面,就会得到如图实现所示的超平面,从实际角度,虚线所示超平面更为合适。
2.线性支持向量机及软间隔最大化
2.1 松弛变量原理
在支持向量机(二)中我们要求支持向量的内侧,也就是靠近分离超平面一侧不允许有样本点存在,现在我们适当放松要求,对于每一个样本点(xi,yi)引进一个松弛变量ξi(ξi>=0),使函数间隔加上松弛变量大于等于1,这样约束条件如下式(1);同时对于每个松弛变量ξi,目标函数由原来的1/2||w||2变为如下式(2),对于式(2)中的C(C>0)称为惩罚参数,由我们根据实际问题人为给定。在这里我们不妨用极限的思维来定性了解一下参数C的作用,当C趋于无穷大时,只有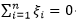 ,才能使得下述(2)式最小,此时即为我们在支持向量机(二)中谈到的线性可分支支持向量机。而当C趋于0时,
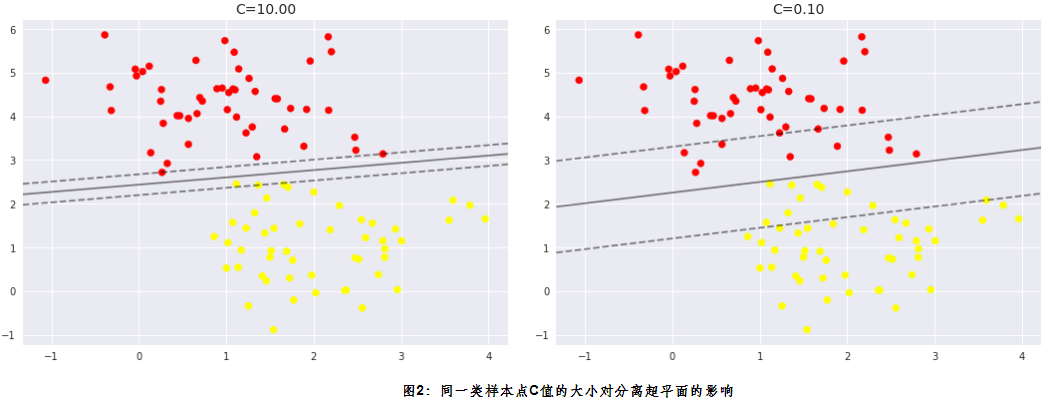
,才能使得下述(2)式最小,此时即为我们在支持向量机(二)中谈到的线性可分支支持向量机。而当C趋于0时,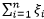 就可以适当的大一点,也就是我们的要求适当的放松了一些。这样我们便可以在模型中通过控制C的大小,来控制我们对分类器模型要求的严格程度,参数C的大小对分离超平面的影响如下图2,由图2可以很直观的看出C值越大,分离超平面对样本数据点划分的越严格,而当C越小时,分离超平面对数据样本点划分越松。
就可以适当的大一点,也就是我们的要求适当的放松了一些。这样我们便可以在模型中通过控制C的大小,来控制我们对分类器模型要求的严格程度,参数C的大小对分离超平面的影响如下图2,由图2可以很直观的看出C值越大,分离超平面对样本数据点划分的越严格,而当C越小时,分离超平面对数据样本点划分越松。
![]()
![]()
2.2 目标函数(原问题)
我们类比在支持向量机(二)中问3的思路使得间隔最大化,在此处即称为软间隔最大化,则一个线性不可分的线性支持向量机的学习问题,变成如下凸二次规划问题
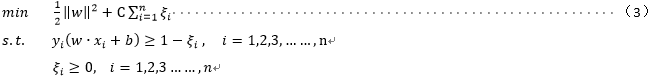
2.3 Lagrange函数及对偶问题
上述(3)条件极值问题对应的Lagrange函数如下:
![]()
构建对偶函数:

将上述(5)(6)(7)式代入(4)式消掉w,b及ξ(具体计算过程可参考支持向量机(二)中式(9))可得对偶问题如下:
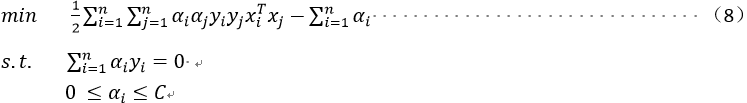
回顾在支持向量机(二)中对偶问题的限制条件为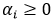 ,而此处与支持向量机(二)中的对偶问题的区别为限制条件由
,而此处与支持向量机(二)中的对偶问题的区别为限制条件由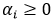 变为
变为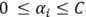 ,原因如下:
,原因如下:

2.4 KKT条件以及参数的几何意义
参照支持向量机(一)中的KKT条件的推导过程,需要满足的条件为如下图:
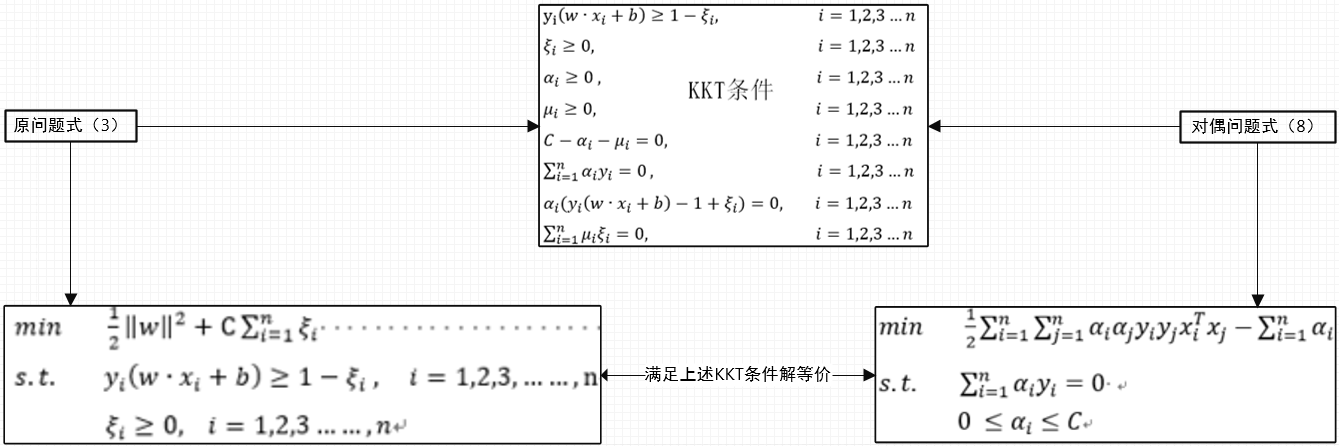
情形1:若某一样本点对应的![]() ,由KKT条件值,其他参数必然满足:
,由KKT条件值,其他参数必然满足:
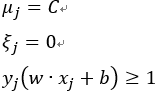
由上述第三个不等式即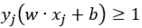 ,可知此样本点在支持向量上或者被分为正确的类别。
,可知此样本点在支持向量上或者被分为正确的类别。
情形2:若某一样本点对应的![]() ,由KKT条件值,其他参数必然满足:
,由KKT条件值,其他参数必然满足:
由上述第三个等式即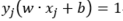 ,可知此样本点必然在支持向量上
,可知此样本点必然在支持向量上
情形3:若某一样本点对应的![]() ,由KKT条件值,其他参数必然满足:
,由KKT条件值,其他参数必然满足:
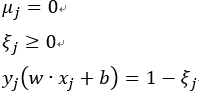
若此时![]() ,说明此样本点正好在支持向量上。
,说明此样本点正好在支持向量上。
若此时![]() ,说明此样本点在支持向量与分离超平面之间,并未穿过分离超平面。也可以理解为此时并未被错误分类
,说明此样本点在支持向量与分离超平面之间,并未穿过分离超平面。也可以理解为此时并未被错误分类
若此时![]() ,说明此样本点正在位于分离超平面上
,说明此样本点正在位于分离超平面上
若此时![]() ,说明此样本点已位于分离超平面另外一侧,可以理解为此样本点已被误分类
,说明此样本点已位于分离超平面另外一侧,可以理解为此样本点已被误分类
2.5 分离超平面求解过程及举例
对于式(8)的求解同支持向量机(二)中的式(10)相似,涉及另外一种优化算法‘序列最小最优化算法SMO在支持向量机(四)中我专门整理记录,此处不做讨论。现我们假设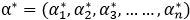 ,是对偶问题式(8)的一个最优解,首先我们可以通过式(5)计算出w*(w*是唯一的)通过满足条件
,是对偶问题式(8)的一个最优解,首先我们可以通过式(5)计算出w*(w*是唯一的)通过满足条件![]() 分量,利用
分量,利用![]() ,显然这里的b*并不唯一我们采用求平均的方式得出最终的b*,下边我们通过《李航-统计学习方法》一书中的一个实例解释w*和b*的计算过程。
,显然这里的b*并不唯一我们采用求平均的方式得出最终的b*,下边我们通过《李航-统计学习方法》一书中的一个实例解释w*和b*的计算过程。
例:输入,训练数据集![]() ,其中
,其中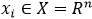 ,
,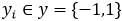 ,i=1,2,3……n;
,i=1,2,3……n;
输出:分离超平面,和分类决策函数。
(1)选择惩罚参数C>0,构造并求解凸二次规划问题
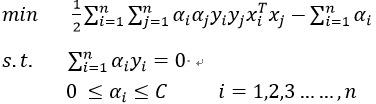
求解上述优化问题得最优解为: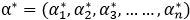
(2)计算![]()
选择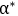 的一个分量
的一个分量![]() ,计算
,计算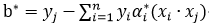
说明:这里的参数的取值范围的原因分析见2.4中情形2
(3)得出分离超平面方程: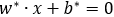
(4)分类决策函数: