概率与期望瞎写

矩母函数

这是解决求形如 \(E(X^i)\) 的问题的利器。

对于一个随机变量 \(X\)，设其矩母函数

\[M_X(t)=E[e^{tX}]\\ = E[\sum_{i=0}^{\infty} \frac{t^iX^i}{i!}]\\ = \sum_{i=0}^{\infty} \frac{E[X^i]}{i!}t^i \]

考虑两个卷积一下。

\[M_X(t)\times M_Y(t)=E[e^{tX}]\times E[e^{tY}]=E[e^{t(X+Y)}]\\ = M_{X+Y}(t) \]

这样，对于一个有多个步骤的期望问题，我们就可以把它拆成一步一步然后乘起来。

常见的矩母函数（贺的）

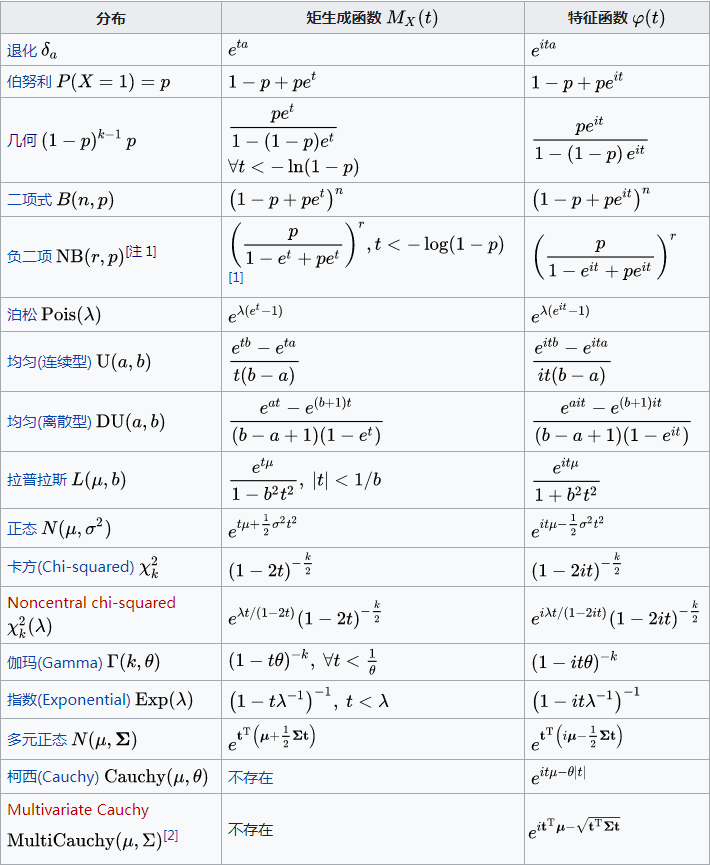
• 退化

变量取值只有 \(a\)，也就是 \(E(X^i)=a^i\)，所以 \(M_X(t)=e^{at}\)

• 伯努利

变量有 \(p\) 的概率是 \(1\)，否则是 \(0\)。

可以发现 \(E(X^i)=E(X)=p\)，但是注意 \(E(X^0)=1\)。所以 \(M_X(t)=1-p+e^{pt}\)。

• 几何

不断进行伯努利，直到出现一次 \(1\) 的期望次数，设 \(q=1-p\)。

\[E(X)=\sum_{i=0}^{\infty} q^ip(i+1)\\ E(e^{tX})=p\sum_{i=0}^{\infty} q^ie^{t(i+1)} \\= pe^t\sum_{i=0}^{\infty} (qe^t)^i \\=\frac{pe^t}{1-(1-p)e^t} \]

• 二项式

进行 \(n\) 次伯努利，\(1\) 的期望个数。

\(n\) 次彼此独立，所以只需要把伯努利卷起来就好了，\(M_{B(n,p)}(t)=(1-p+e^{pt})^n\)。

• 负二项式

不断进行伯努利，直到出现 \(n\) 次 \(1\) 的期望失败次数。

只是把上面几何分布式子中的 \(i+1\) 变成 \(i\)，然后 \(n\) 个卷起来，得到 \(M_{NB(n,p)}(t)=(\dfrac{p}{1-(1-p)e^t})^n\)。

然后不会了，先咕着。

ARC154F

就是求最后的一个矩母函数了，可以发现这个过程可以分成 \(n\) 步，第 \(i\) 步是已经有了 \(i\) 个不同的面，要扔出第 \(i+1\) 个面，这是个几何分布，成功概率为 \(p=\frac{n-i}{n}\)，其矩母函数是

\[M_X(t)=\frac{pe^t}{1-(1-p)e^t} \]

然后相当于是 \(n\) 个东西乘起来。

把 \(e^t\) 看成是主元，就可以得到乘起来的结果 \(\dfrac{P(e^t)}{Q(e^t)}\)。

如果把上下的 \(e^t\) 分别拆开了，那就只需要求这个东西的前 \(m\) 项，多项式求逆即可。

考虑 \(P(e^t)\) 本质上是一个 EGF，把它变成 OGF。

\[P(e^t)=\sum p_ie^{it}\\ \text{EGF}(e^{it})=\text{OGF}(\frac{1}{1-it})\\ F(e^t)=\sum \frac{p_i}{1-it} \]

\(F\) 就是需要求的 OGF 了，直接分治 FFT 即可。

code