网络流乱做

感觉建图还是比较有迹可循的，所以记录一下。

约定下面的图中边权表示流量，如果是二元组，第二位表示费用，\(S\) 表示源点，\(T\) 表示汇点。

part 1 最大流

前置知识

• 最大流算法，dinic 或者 Ek 都可，模板，本质上是一个反悔贪心的过程，复杂度比较大，但是基本跑不满。

part 1.1 二分图匹配模型

P3386

考虑每个点只能用一次，因此直接按匹配建图即可。

part 1.2 拆点

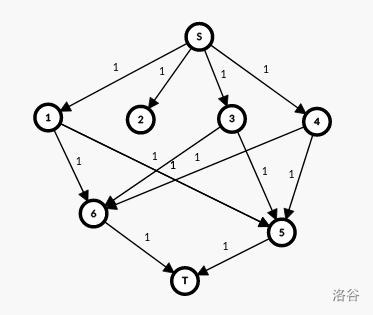
一个比较常用的套路，由于在一般的最大流中无法限制点的流量，因此可以把一个点拆成一个入点，一个出点，中间连一条边，用这条边来限制流量。

如果这个点是直接流向源点或者汇点的，可以直接用这条源汇边来限制流量，就和上面的二分图匹配一样。

P1361

每一个格子都有通过蜥蜴数量的限制，因此拆点一下，源点连向所有初始有蜥蜴的点，如果一个格子可以走出图就连向汇点跑最大流即可。

code

part 1.3 网格模型

对于网格在 \(n\times m\) 的网格上取数的的问题。

• 可以考虑染色，这样变成二分图匹配问题。

• 可以考虑对于行列分别建点，用边表示中间的格子，这样能使点数大大降低。

acwing374

直接对网格进行黑白染色，这样可以发现每个点只会和周围的四个点匹配，那么二分图匹配即可。

acwing375

对于行列分别建点，一个可以放棋子的地方就在对应的行列之间建一条边，流量限制为 \(1\)，跑最大流即可。

code

ABC205F

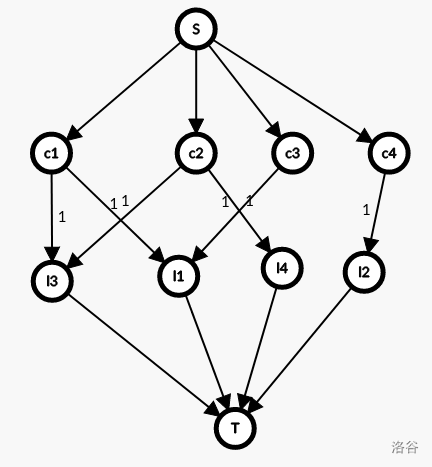
在上一题的基础上增加了一个放棋子的限制，那么对于一个棋子拆点来限制流量即可。

code

part 1.4 最小链覆盖模型

已知一张 DAG，求用最小数量的链将其覆盖，要求两条链不能在节点处有交。

相当于在 DAG 上选若干条边，组成一条条链，但要求每个点入度出度最大是 \(1\)，最小链的数量就是点数减去选的边数。

那么按照这个限制就可以建图，把每个点拆成入度和出度两个点，然后二分图最大匹配即可。

如果可以在节点出有交，那么就是入度等于出度，这个难以限制，只能把图改一下，让每一个点都连向他所有的后继，这样再跑点不能相交的情况即可。

ABC237Ex

先暴力枚举所有子串，按包含关系建一张 DAG，那么问题变成求最长反链。

最长反链 = 可以重复经过点的最小链覆盖，直接跑二分图最大匹配即可。

part 2 最小割、对偶图

前置知识

• 最小割 = 最大流，这个可以从增广路上理解。

part 2.1 最小割可行边、必须边以及构造

先跑一下网络流，在如果一条边可能在最小割中，显然它需要是一条满流边。

因此在残余网络上，把非满流边拿出来建图，强连通分量跑一下，那么在一个联通分量内的边显然没有用，因为删和不删一样烂。

否则连接两个不同分量的满流边就是可行边，连接 \(S\) 和 \(T\) 联通分量的边是必须边。

构造方案直接把 \(S\) 所在的联通分量抠出来，两部分中间的边就是割掉的边。

P4126 板子。

part 2.2 二分图相关

在来考虑一下二分图匹配模型。

其最大流就是最大匹配，考虑其最小割，显然割去与源汇点的边一定不劣，然后选出割掉代表点的边后，相当于这些点覆盖了所有的边。

所以二分图最大匹配=最小点覆盖。

part 2.3 对偶图

P4001

已知平面图，求最小割。

把图中每一块空的区域看成一个点，然后相邻区域连边，边权就表示割掉这条边的代价，那么最小割就变成了一头到另一头的最短路。

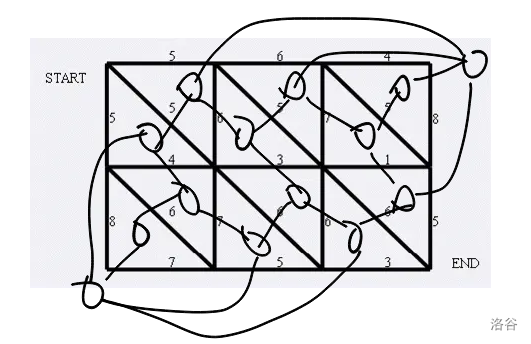
右上角到左下角求一个最短路即可。

P2046 一样的题。

P7916

\(k=2\) 的情况和上面那题一样。

\(k\) 不是很大，考虑最后相当于用一些路径把图变成几个部分，但是注意这些路径可以不交。

然后简单了，直接区间 dp，连一条最短路相当于把当前区间分成几个不干扰的部分。

part 2.4 网格模型

染色，染色。

P2774

黑白染色，相当于选相邻两个就不合法，也就是相邻两个之间至少断掉一个，那么源点连向所有白点，白点连向相邻黑点，黑点连向汇点即可。

CF1517G

直接枚举所有情况

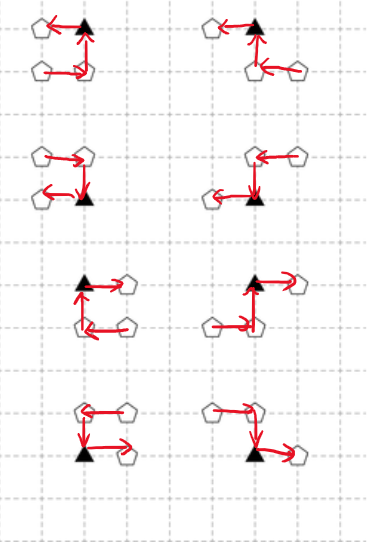
图是贺的。

可以发现对网格进行四染色，即 \(c_{i,j}=(i+j)\bmod 4\) 之后，四个合法的帐篷就是在走一条 \(0,1,2,3\) 的路径。

因此颜色为 \(c\) 的直接连向周围 \(c+1\) 的点，相当于至少断掉一个。

part 2.5 最大权闭合子图

最阴间的来了。

就是选一个点有一定收益，但是同时满足条件需要代价。

常用套路是全部加起来减去使条件满足的最小割，得到最大收益。

P2762

板子，总和就是全部收益加起来，然后实验连向对应的仪器，联通表示不合法，要么取消这个实验，割去 \(p_i\)，要么选用所有仪器，割去对应所有的 \(c_i\)。

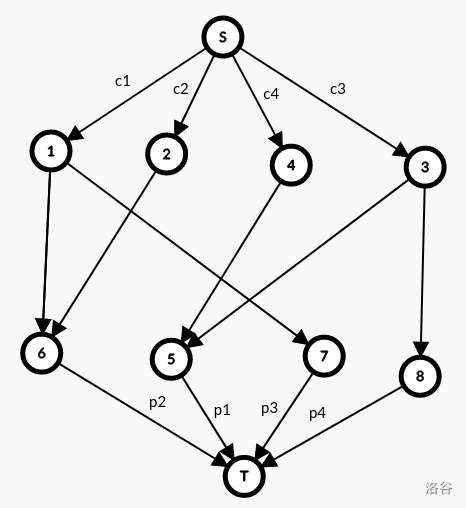
最小割即可。

arc107F

这个不太一样，主要是因为点权有正有负。

但还是类似，在一个联通分量里的点相当于是在正数和负数中选择一个，全部删掉，因此正数连源点，负数连汇点，然后拆点来表示不选这个点，然后直接维护联通即可。

code

part 2.6 k-sat 模型

拆点来表示一个点的每个数值，这样可以满足不等式条件。

ABC224H

正解是线性规划，考虑一个 \(c_{i,j}\le 10\) 的弱化版。

设 \(a_i,b_i\) 分别表示选择的个数，那么代价就是 \(\sum a_i\times L_i+\sum b_i\times R_i\)，需要满足的条件就是 \(a_i+b_j\ge c_{i,j}\)。

把一个点拆成 \(11\) 个点，连成一条链，断掉其中一条边就表示选对应的 \(a_i\)，那么显然需要满足 \(b_j\ge c_{i,j}-a_i\)，因此直接连边即可，边权就是 \(a_i\times L_i\)。

code

part 3 费用流

前置知识

• 费用流

模型好像和上面的都差不多，来几个新的。

part 3.1 带权最小链覆盖

P1251

显然纸巾全部在开始的时候买，然后向后面流，但是无法限制每个点都要选。

考虑和不带权东西类似，因为每个点都要选，因此出度必然有点，这样只需要满足每个出度点就好了。

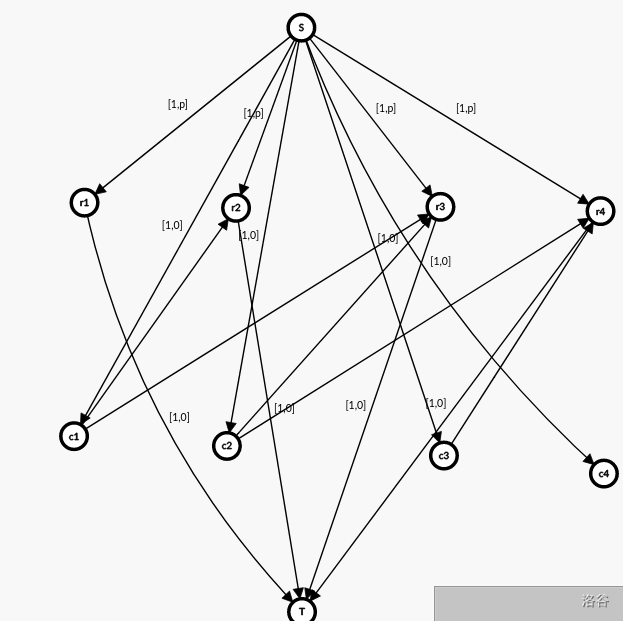
但是这个东西也可以贪心，由于费用流的费用是凸的，所以可以三分一下开始买了多少个，然后用队列维护贪心即可。

code

P4542

一样的题，人之间本质无影响，只不过需要预处理一个最短路即可。

但是如果不要求每个点必须走，而要求走的点数尽量多的前提下花费少呢？

直接拆点，把点权设为 \(-\infty\)，然后经过一个点就是选了这个点即可。

part 3.2 动态加点优化建图

P2050

暴力建图很简单，把厨师拆成 \(\sum p_i\) 个，然后二分图带权匹配即可，点数爆炸。

但会发现很多点都没有用，可以发现每次只流 \(1\) 点流量，流到哪一个厨师哪里就把他的点数增加即可。

但是这样的题目很少，一般的题目不是很好动态加点。

part 3.3 区间覆盖模型

P3980

区间覆盖不太好搞，一个基本的想法是区间向对应的每个点连边，但是这样难以维护每个点流 \(1\)。

换一个思路，考虑先连一条链，用中间的边表示每个点，然后 \(l_i\) 向 \(r_i\) 连边，这样就相当于流过链上的边的流量是不大于 \(-k_i\) 的，但是由于流量有负数，整体加上 \(+\infty\) 即可。