9月杂题选做

上回说到：2022.8

关于难度

\(\color{gray}\bigstar\) 可以秒杀的题。

\(\color{green}\bigstar\) 思考一会儿后可以秒的题。

\(\color{blue}\bigstar\) 需要较长时间思考的题。

\(\color{Gold}\bigstar\) 看题解、稍加指点就会做的题。

\(\color{red}\bigstar\) 看题解后需要较长时间消化，甚至现在都没有完全理解的题。

---

ABC266Ex *2865 \(\color{blue}\bigstar\)

有 \(n\) 个点，第 \(i\) 个点在 \((x_i,y_i)\) 在第 \(t_i\) 时刻会出现 \(a_i\) 个球然后下一个时刻消失，现在有一个人在 \((0,0)\)，每个时刻可以向上左右走，但不可以向下走，求最多拿几个球。

\(n\le 10^5\)。

不是很难的题。

考虑设 \(f_i\) 表示最后一个拿的球是 \(i\) ，最多可以拿多少个球，那么考虑 \(i\) 可以向 \(j\) 转移的条件是什么，可以列一下：

\[\begin{cases}y_i\le y_j\\t_i\le t_j\\ |x_i-x_j|+y_j-y_i\le t_j-t_i \end{cases} \]

然后考虑如果 \(t_i>t_j\)，第三个等式右边 \(<0\)，显然不合法，因此这个条件可以扔掉。

然后考虑绝对值的意义，就是 \(|a-b|=\max(a-b,b-a)\)，所以可以直接拆成两个式子，然后可以得到：

\[\begin{cases}y_i\le y_j\\ x_i-x_j+y_j-y_i\le t_j-t_i\\ x_j-x_i+y_j-y_i\le t_j-t_i \end{cases} \]

移项一下，就可以发现本质上是一个关于 \(i,j\) 的三维偏序，因此考虑 cdq。

直接先做左边，然后考虑左边转移右边的，再做右边的。注意转移完了序列需要回复到开始状态。

code

---

ARC051D *2779 \(\color{blue}\bigstar\)

有一个 \(n\times m\) 的矩阵，\((i,j)\) 上写有数字 \(a_i+b_j\)，\(Q\) 次询问，每次询问左上角一个子矩形，求这个子矩形的子矩形内数和的最大值。

\(n,m,Q\le 2000\)。

考虑相当于选 \(a,b\) 各一个区间，对于同样的区间长度显然选和最大的，假设 \(f_i,g_i\) 分别表示行，列上连续 \(i\) 个数的最大值，这个可以 \(O(n^2)\) 预处理，然后考虑如果选了 \(f_i,g_j\)，答案就是 \(f_i\times j+g_j\times i\)，咋求最大值呢。

这个东西不是很好搞，考虑整体除以 \(i\)，变成 \(\frac{f_i}{i}\times j+g_j\)，这是一个关于 \(\frac{f_i}{i}\) 的一次函数，可以直接李超树维护，也可以斜率排序后直接整体二分做。

总复杂度 \(O(n^2\log n)\)。

code

---

ARC147D *2145 \(\color{green}\bigstar\)

题比较长，自己看吧。

考虑两个相邻的集合是删掉一个或者加上一个，那么直接对于每个空隙里标上一个数 \(x\) 表示 \(S_i\) 到 \(S_{i+1}\) 状态改变，那么考虑对于一种标数方案，相当于只需要确定 \(S_1\) 中是否有即可，如果 \(S_1\) 中有 \(i\)，那么总共出现 \(a_i\) 次，那么如果 \(S_1\) 中没有就会出现 \(n-a_i\)，所以总贡献可以直接求和，就是 \(\prod_{i=1}^m (a_i+n-a_i)=n^m\)。

因此最后的答案就是 \(m^{n-1}\times n^m\)，快速幂即可。

code

---

CF1716F *2500 \(\color{blue}\bigstar\)

有 \(n\) 个袋子，每个袋子里面有编号为 \(1...m\) 的球各一个，现在每个袋子里面选一个球，定义选出的编号为奇数的球的个数是 \(F\)，求 \(F^k\) 之和对 \(998244353\) 取模。

\(n,m<998244353,k\le 2000\)。

设 \(t\) 表示 \([1,m]\) 奇数的个数，那么暴力式子可以直接枚举选了多少个奇数。

\[\sum_{i=1}^n t^i(m-t)^{n-i}\binom{n}{i}i^k \]

后面有一个 \(i^k\)，\(k\) 很小，一眼斯特林一下。

\[= \sum_{i=1}^n t^i(m-t)^{n-i}\binom{n}{i}\sum_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix}\binom{i}{j}j!\\ = \sum_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix}j! \sum_{i=j}^n\binom{n}{i} \binom{i}{j}t^i(m-t)^{n-i}\\ = \sum_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix}j! \binom{n}{j}\sum_{i=j}^n\binom{n-j}{i-j}t^i(m-t)^{n-i} \]

此时后面可以改成枚举 \(i-j\)，那么右边那个就和二项式定理差不多，但是后面两个指数和为 \(n\)，不行，所以可以把 \(t^j\) 提到前面来。

\[=\sum_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix}j! \binom{n}{j}t^j\sum_{i=0}^{n-j}\binom{n-j}{i-j}t^{i-j}(m-t)^{n-i}\\ =\sum_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix}j! \binom{n}{j}t^jm^{n-j} \]

然后直接求即可。

code

---

gym101620D \(\color{blue}\bigstar\)

题比较长，自己看吧。

题解是线段树，但是我有高妙分块。

考虑修改一个点权本质上就是修改这个点的出边以及其他点到这个点的边，那么考虑走 \(k\) 步这个东西不好搞，应该多次跳，找到环就停止。

用之前一个题类似的做法，可以直接把横坐标分块，设块长为 \(B\)，那么记录 \(nex_{i,j}\) 表示从 \((i,j)\) 出发走到下一个块的哪一个位置，这样跳的话复杂度为 \(O(\frac{nm}{B})\)，然后考虑修改，修改一个点会改变的 \(nex\) 区域是一个前面的一个区域，直接暴力修改即可，复杂度 \(B^2\)，平衡一下复杂度，\(B=\sqrt[3]{nm}\) 时最优，复杂度为 \(O(Q(nm)^{\frac{2}{3}})\)，可过。

code

---

CF1580B *2600 \(\color{Gold}\bigstar\)

求有多少个长度为 \(n\) 的排列满足恰好有 \(k\) 个数满足所有包含这个数的区间的最大值恰好有 \(m\) 个。
\(n\le 100\)。

\(O(n^5)\) 过，流汗黄豆。

巧妙的思路是笛卡尔树，那么不同的最大值数量就是一个点的深度，相当于求深度为 \(m\) 的点恰好有 \(k\) 个的二叉树数量。

这个可以直接二叉树 dp，比较简单。

code

---

CF1718C *2400 \(\color{Gold}\bigstar\)

题比较长，自己看吧。

一个典中典结论是每次跳 \(k\) 步等价于每次跳 \(\gcd(k,n)\) 步，所以可以得到：

\[(s,k)=\gcd(k,n)\times (\sum_{j=0}^{n-1} [j\equiv s\pmod {\gcd(k,n)}]a_j) \]

可以直接枚举因数进行统计，复杂度 \(O(n\sqrt{n}\log n)\)，寄。不会了。

正解比较牛，就是说考虑每次跳 \(k\) 步，找到一个数满足 \(d|k\)，那么选 \(d\) 一定比选 \(k\) 优，因为一个序列中一定有一个子序列满足平均数大于整个序列。

因此只需要对每个质数做就好了，复杂度 \(O(n\log^2 n)\)。

code

---

CF802N *2400 \(\color{green}\bigstar\)

题比较长，自己看吧。

先想了一下 dp，发现不太能搞。不知道为啥就想到了费用流。

一个简单的暴力流是这样的

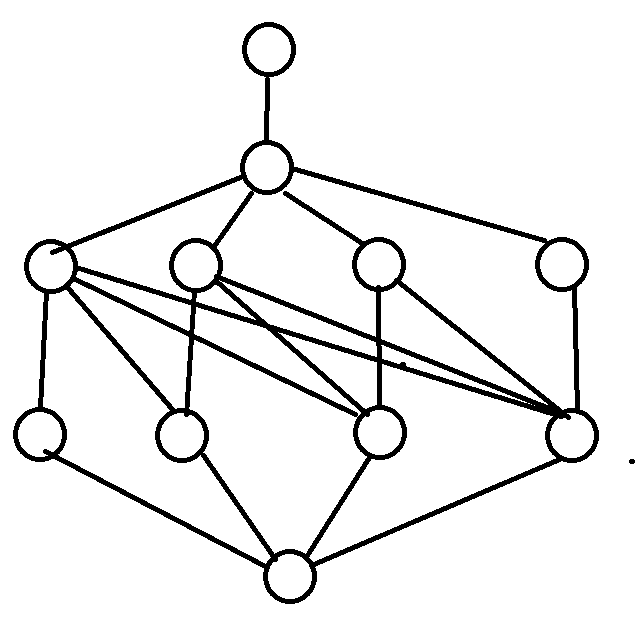
最上面是限定流量为 \(k\)，然后是流向每个生产点，流量为 \(1\)，费用是 \(a_i\)，中间每天向后面的天连边，然后流向终点，费用是 \(b_i\)。

可以发现中间的点流量无限，费用为零，考虑直接优化建图：

code

---

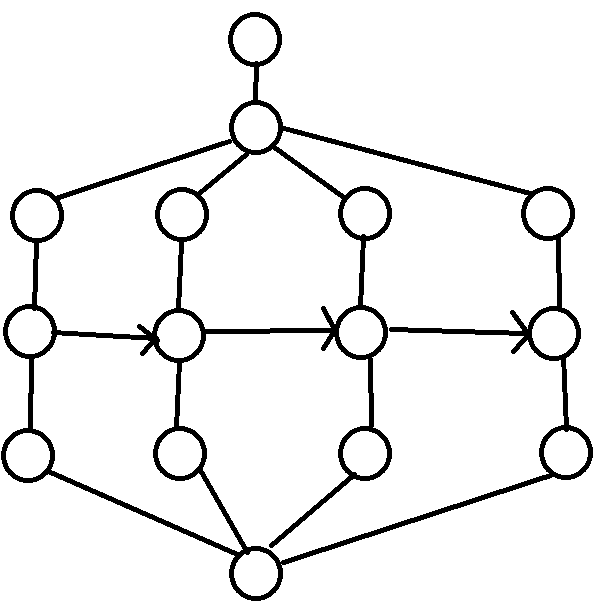
CF990G *2400 \(\color{green}\bigstar\)

给一棵 \(n\) 个点的树，点有点权 \(a_i\)，定义 \(g(x,y)\) 表示 \(x\) 到 \(y\) 路径上点的点权的 \(\gcd\)，对于每个 \(1\le i\le 2\times 10^5\)，求有多少条路径满足 \(g(x,y)=i\)。

\(n\le 2\times 10^5\)。

考虑先求出是 \(i\) 倍数的方案数，然后简单容斥一下就好了。

那么这个东西相当于一个子图求路径数，可以把边拿出来然后用并查集维护，复杂度就是 \(O(n\sqrt{n})\)。

code

有一个类似的题是 ABC248 *2514，乘上一个路径长度，改成换根 dp 即可。

code

---

CF 好像大家都可以到洛谷上看翻译，那么翻译就懒得放了（。

---

CF1152E *2400 \(\color{green}\bigstar\)

有一个知名的东西是 \(a+b=\min(a,b)+\max(a,b)\)，同理，\(b_i\) 与 \(c_i\) 就对应着两个相邻的 \(a\)，如果 \(b_i>c_i\) 显然无解，否则就考虑 \(b_i,c_i\) 连边，然后就相当于是一个欧拉路了，直接做即可。

code

---

CF1333E *2400 \(\color{blue}\bigstar\)

首先 \(n\le 2\) 显然是无解。

然后去构造 \(n=3\)，构造半天构造了：

\[\begin{matrix}6&5&9\\7&2&3\\1&4&8\end{matrix} \]

就是把后困在了 \((2,1)\) 位置。

然后考虑大的怎么构造，只需要一圈一圈得走，最后走到这个 \(3\times 3\) 的里面的 \(1\) 处即可。

code

---

CF758F *2400 \(\color{green}\bigstar\)

考虑去枚举公比 \(\frac{p}{q}(\gcd(p,q)=1)\)，然后考虑如果设第一个数是 \(kp^n\)，那么最后一个数就是 \(kq^n\)，一个简单的想法是直接枚举 \(p,q\)，但是会寄，所以先把 \(n\le 2\) 的情况直接特判掉，然后可以发现 \(p,q\) 只需要枚举到 \(\sqrt{n}\) 级别就可以了。

然后已知 \(p^n,q^n\)，就可以直接算答案了。

code

---

CF911F *2400 \(\color{green}\bigstar\)

树上两点距离之和最大，离一个点距离最大的点就是直径的两个点，因此直接把直径跑出来然后先把其他点删完，然后删直径即可。

code

---

CF1726E *2400 \(\color{blue}\bigstar\)

逆排列，直接考虑置换环，一个置换环上显然 \(p_i,p_i^{-1}\) 就对应着 \(i\) 的左右两个数，也就是每个环上距离为 \(2\) 的两个点差值 \(\le 1\)。

简单列举一下可以发现只有 \(\{i\},\{i,j\},\{i,j,i+1,j+1\}\) 这三种情况，第三种情况有两种方法。

可以先考虑只有前两个，比较好做，就是直接考虑加入一个数，是否与前面的构成环即可，可以得到

\[ g_ { i } =g_ { i-1 } + ( i-1 ) g_ { i-2 } \]

然后考虑第三个怎么搞，首先不能像上面那样递推，因为前面的两个可能会把其他选 \(4\) 个方案中连续两个拆散，所以可以直接枚举选多少个 \(4\)。

式子是

\[\sum_{4i\le n}\binom{n-2i}{2i}\frac{(2i)!}{2^ii!}g_{n-4i}2^i \]

直接算即可，复杂度 \(O(Tn)\)。

code

---

打了 arc147，过了 ABCD ，E 真的是 sb 题，赛后很快就会了，输麻了。

---

ARC147D *2145 \(\color{green} \bigstar\)

题比较长，自己看吧。

就是考虑既然两个集合之间相差一个，那么就在两个集合中间放这个不同的数，有 \(m^{n-1}\)，然后相当于考虑第一个集合有那些数即可。

本质上就是一个异或的过程，可以发现如果设第一个集合有 \(x\)，\(x\) 的出现次数是 \(a\)，那么没有 \(x\)，出现次数就是 \(n-a\)，若干个这个东西乘起来，容易发现就是 \(n^m\)。

答案就是 \(n^m\times m^{n-1}\)。

code

---

ARC145E *2553 \(\color {blue} \bigstar\)

有 \(n\) 个人，第 \(i\) 个人考了 \(a_i\) 分，目标分数是 \(b_i\) 分，合法条件是所有 \(i\) 满足 \(a_i\ge b_i\)，可以进行若干次操作，每次操作选择两个人的分数然后交换，求对于所有合法方案，最多有多少个人满足没有被交换。

\(n\le 3\times 10^5\)。

其实不是很难，考虑排序后把 \(a_i\) 看成是减一，\(b_i\) 看成是加一，那么就相当于是前缀都不小于 \(0\)。

考虑每次删掉一个区间相等于是区间减，一眼贪心，直接右端点排序后贪心选就可以了。

code

---

ARC148D *2009 \(\color{blue}\bigstar\)

题比较长，自己看吧。

考虑 Alice 最后操作可以在两个数中选一个，也就是需要满足最后两个数 \(a-b=b-a\)，那么只有两种情况，\(a=b\)， \(a-b=\frac{m}{2}\)。

考虑如果一个数出现了多次，那么 Alice 选这个 Bob 肯定也选这个，也就是出现次数可以模 \(2\)。

考虑剩下的数，如果 \(m\) 是奇数，那么剩下有数就 Alice 必胜，否则 Bob 胜。

如果 \(m\) 是偶数，相当于 \(i\) 和 \(i+\frac{m}{2}\) 匹配，那么如果没有匹配完就 Alice 赢。

否则，如果匹配数量是奇数，那么还是 Alice 赢。

剩余情况 Bob 赢。

code

---

ARC104E *2824 \(\color{blue}\bigstar\)

有一个序列 \(a\)，\(a_i\) 在 \([1,x_i]\) 范围内随机生成，求最后序列最长上升子序列的期望长度。

\(n\le 6,x_i\le 10^9\)。

\(n\) 这么小，容易想到去枚举 \(n\) 个数的排名，就是个全排列，然后对于每个全排列，先求出最长上升子序列，然后就变成每个数取值为 \([1,x_i]\)，求单调上升的方案数，这个是典，然后就可以直接做了。

注意可能会有两个数相等的情况，这种情况应该算在编号小的值大的那个排列中，因为对后面的没有贡献，中间组合数部分 \(n\) 很大，但是 \(m\) 很小，可以直接暴力算，复杂度 \(O(n^4n!)\)。

code

---

CF847J *2400 \(\color{green}\bigstar\)

感觉不是很难，注意到 \(m\le 5000\) 而不是 \(n^2\)。

先考虑二分一下，然后可以发现相当于 \(x,y\) 中选一个数减一，可以考虑网络流，那么直接原点向每个点连二分的值的边，然后每个边建一个点，链向对应的两个点，然后连终点即可。

本质上就是每条边要选一个点来流 \(1\) 的流量。

code

---

CF1109D *2400 \(\color{gray}\bigstar\)

ez 题，直接枚举中间放多少条边，然后计算放到中间的方案数，就是一个插板法即可，然后把中间这条链看成一个整体，那么就是一个 prufer 经典题了，直接做即可，式子是：

\[\sum_{i=1}^{n-1} \binom{m-1}{i-1}\binom{n-2}{i-1}(i-1)!(i+1)n^{n-i-2}m^{n-1-i} \]

code

---

CF825G *2500 \(\color{green}\bigstar\)

考虑查询一个点，不能走到的点就是以这个点为根，然后若干个子树是不能走到的。

转化到于原来的树上，也就是若干个子树加上根那里可能有一个连通块。

一个简单的想法是拿第一个操作的点当做根，这样就只有子树了，相当于没有一个黑点的极大子树然后去加上查询点到根上的最小值。

前面的可以对于每个修改，加上这个修改的点到根的最小值即可，查询一样。

因此直接维护 \(f_x\) 表示 \(x\) 到根上所有点的最小值，不知道为什么一定要用快读才可以过。

code

---

ARC106E *2825 \(\color{blue}\bigstar\)

有 \(n\) 个人，第 \(i\) 个人上 \(a_i\) 天班，休息 \(a_i\) 天，如此反复，每天可以给一个上班的人发一个奖章，求至少多少天后满足每个人都有至少 \(k\) 个奖章。

\(n\le 18,a_i,k\le 10^5\)。

有趣的题。

这个至少，先考虑一个二分答案，容易发现答案的取值是 \([nk,2nk]\)，如何判定是否合法。

有一个简单的做法，就是考虑网络流，源点向每个人连 \(k\) 的流量。

然后每个人向上班的天连边，然后每天向汇点连 \(1\) 的流量边。

网络流显然寄，考虑模拟网络流。

先转化为最小割。显然就是割掉一些人，然后剩下的人连向的所有天都需要割掉，然后这个东西可以考虑记录每天有哪些人连向它，集合是 \(S\)，那么对这个开个桶记录一下，然后就是这样的一个计数问题。

\[f_x=\sum_{x\cap y\ne \empty} g_y \]

直接容斥一下，设

\[h_x=\sum_{x\in y} g_y \]

那么得到

\[f_x=\sum_{y\in x}(-1)^{cnt(y)}h_y \]

code

---

ABC269G *2440 \(\color{gray}\bigstar\)

把 \(b_i-a_i\) 看成物品，那么不同的物品最多只有 \(\sqrt{n}\) 个，直接分组背包就好了。

code

---

ARC108E *3101 \(\color{Gold}\bigstar\)

有一个长度为 \(n\) 的排列 \(p\)，一个合法的标记方案是标记一些数满足单调递增，现在每次在标记后序列合法的数中随机选择一个标记，求最后标记数的个数的期望值。

\(n\le 2000\)。

考虑把数放在二维平面上，容易发现标记一个数之后，剩下所有的数都只能放在这个数的左下角或者右上角，那么合法的区域就是若干个从左下到右上的矩形。

可以发现矩形之间互相不影响，因此可以分别计算然后加起来。

一个简单的 dp 想法就是考虑设 \(f_{i,j}\) 表示矩形左边是 \(i\)，右边是 \(j\)，在这个矩形中选的期望长度，只需要枚举中间选哪一个数即可，中间这个数 \(k\) 需要满足 \(p_i<p_k<p_j\)，容易得到一个 \(O(n^3)\) 的 dp。

code

优化不会了。

考虑中间这个东西实际上是一个偏序关系，因此可以采用树状数组直接简单维护。

code

---

突然发现必须写 codechef 了，停止 lynkcat 的随意搬题行为。

感觉题目质量不错，一个优势是许多题有中文。

做了一下题，感觉 3000- 的题都是**题，所以从 3000 开始做。

我毕竟是天竺来的猴子，还是要多做做我印度祖国的题目。

---

MAKEODD *3002 \(\color{green}\bigstar\)

一个序列 \(a\)，令 \(f(a)\) 表示进行若干次操作，每次操作选择一些数除以一个二的幂次（都需要整除），把所有数变成奇数的最小次数。

现在已知一个序列 \(b\)，求 \(b\) 所有子串 \(a\) 的 \(f(a)\) 之和。

\(n\le 10^5,a_i\le 10^6\)。

显然每个数变成 \(x\times 2^k\) 的形式，然后就相当于区间减，变为 \(0\) 的最小次数。

容易发现同一个次幂出现多次是一样的，因此可以并在一起。

可以设 \(g(S)\) 表示有 \(S\) 这个集合的次幂的最小操作次数。

考虑区间，容易发现右端点固定后 \(S\) 值不同的左端点只有 \(\log a_i\) 个，直接枚举减即可。

code

---

SEATR *3003 \(\color{green}\bigstar\)

？？？明明 \(O(n)\) 可以过，为什么 \(n\le 80\)？std 做法是什么 sb。

已知度数，可以先给每个点标号，度数相同的点标号无顺序。然后用 prufer 生成树，钦定一个根，然后相当于每个点的贡献就是儿子个数的阶乘，全部乘起来即可。

code

---

ARC108F *2646 \(\color{green}\bigstar\)

看到树上距离最大一下想到直径。

直接找到直径两个端点，如果同色那么显然答案就是直径。

否则异色，跑出每个点到两端点距离，然后直接计数比较 hard，考虑求出对于每个 \(i\)，有多少种方案长度 \(\ge i\)。

这个东西可以把点分成 \(3\) 类，到两端点距离都超过 \(i\)，只有一个超过，都没有超过，然后直接计数即可。

code

---

TCKTMACHINE *3204 \(\color{Gold}\bigstar\)

有 \(m\) 个座位，有 \(n\) 个团队，第 \(i\) 个团队需要在 \([l_i,r_i]\) 中占 \(a_i\) 个座位，求对于每个 \(1\le i\le n\)，求一个最大的 \(r\)，满足 \([i,r]\) 所有团队都可以满足需要。

\(n\le 2\times 10^5,m\le 10^9,l_i\le l_{i+1}\)

先考虑已知一个区间如何判断合法，容易发现直接按右端点排序，然后相当于每次贪心放左边，这个东西可以用线段树二分维护。

但是这个东西很阴间，而且不好用双指针维护，也就是不太好删除。

从左向右考虑每一个座位，把所有可以坐这个座位的人放在一个堆里，每次取一个右端点最小的即可，正确性显然。

接下来考虑从右向左考虑，因为从右向左就满足了上面的贪心策略，然后每次把这个团队所占的位置设成 \(r_i\)，容易发现插入一个团队时只需要放入\(a_i\) 个 \(r_i\)，然后排序即可，这样不满足条件的就是在这个序列上存在一个数大于其下标。

code

---

STTT *3206 \(\color{blue}\bigstar\)

考虑一个子树可能会与其他子树 \(\gcd>1\)，那么显然只需要记录该子树中出现的素数集合，如果合并两个子树是发现都出现了一个素数就寄。

但是 \(<70\) 的素数有 \(19\) 个，存不了。

考虑两个子树需要相等，显然这个素数需要满足 \(2p<n\)，否则不存在，也就是 \(35\) 以内的素数，只有 \(11\) 个。

然后直接树上背包即可，然后可以发现 \(11\times 11\times 2^{11}>3^{11}\)，所以子集卷积需要暴力卷。

code

---

CF543C *2500 \(\color{blue}\bigstar\)

想了很久，一开始以为是按行进行 dp，然后发现根本不可做。

本质上就是考虑对于一个串来说要找到一个字符使得和其他都不一样， 那么要么修改这个字符，要么修改这一列相同的其他所有的字符。

因此考虑按列进行 dp，设 \(f_{i,S}\) 表示前 \(i\) 列，满足条件的字符串的集合为 \(S\) 的最小代价，那么要么修改单个，要么把相同字符的一起做，这就是一堆物品，直接背包即可。

code

---