q-binomial 学习笔记

主要可以解决一些生成函数问题，对于 \(q^jx\) 这样形式的式子可以有效处理，网上资料不是很多，orz zaky的博客。

part1 q-Binomial

考虑一个很经典的模型，就是从 \((0,0)\) 出发，每次向上或者向右走一格，走到 \((n,m)\) 的方案，这个方案数显然就是 \(\binom{n+m}{m}=\binom{n+m}{n}\)。

考虑比如 \(n=2,m=2\)，可以得到下面一些行走路线，这些图被称为 Ferrers diagrams，直译过来就是费勒斯图。

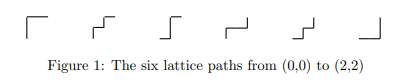
考虑这些行走路线右上角的部分有几个方格。

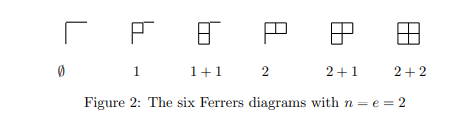
然后此时去定义这个 q-binomial，假设对于上面一种情况右上角方格数为 \(a_i\)，那么定义 \(\begin{bmatrix}n+m\\m \end{bmatrix}_q=\sum q^{a_i}\)，比如对于上面的例子，\(\begin{bmatrix}4\\2 \end{bmatrix}_q=1+q+2q^2+q^3+q^4\)。

此时考虑这个东西怎么去递推，令 \(q\) 为一个常数，\(f_{n,m}\) 为此时的值。

考虑上面格子的问题本质上是求一个长度为 \(m\) 的序列 \(b\)，满足 \(b_i\le n,b_i\ge b_{i-1}\)，然后答案就是 \(\sum_b q^{(\sum_{i=1}^m b_i)}\)，那么直接 dp，那么 \(f_{i,j}\) 就表示前 \(i\) 个数，最后一个 \(\le j\) 的总和，那么容易得到转移方程：

\[f_{n,m}=f_{n,m-1}+f_{n-1,m}\times q^m \]

那么可以得到

\[\begin{bmatrix}n+m\\m \end{bmatrix}_q=\begin{bmatrix}n+m-1\\m-1\end{bmatrix}_q+q^m\begin{bmatrix}n+m-1\\m \end{bmatrix}_q \tag{1} \]

\[\begin{bmatrix}n\\m \end{bmatrix}_q=\begin{bmatrix}n-1\\m-1\end{bmatrix}_q+q^m\begin{bmatrix}n-1\\m \end{bmatrix}_q \]

然后还有个小推论：

\[\begin{bmatrix}n+m\\m \end{bmatrix}_q =\begin{bmatrix}n+m\\n\end{bmatrix}_q\tag{2} \]

和组合数类似的式子，证明简单，考虑前面 \(n\times m\) 的矩形的意义即可，相当于旋转一下。

然后考虑 \(\begin{bmatrix}n\\m \end{bmatrix}_q\) 这个东西怎么求通项，当 \(q=0\) 时，显然 \(\begin{bmatrix}n\\m \end{bmatrix}_0=\dbinom{n}{m}\)。

结论是

\[\begin{bmatrix}n\\m \end{bmatrix}_q =\frac{\prod_{i=n-m+1}^n (1-q^i)}{\prod_{i=1}^m (1-q^i)}\tag{3} \]

为了简记，定义 \([n]_q=\sum_{i=0}^{n-1}q^i,[n]!_q=\prod_{i=1}^n [n]_q\)，那么可以发现

\[[n]_q=\sum_{i=0}^{n-1}q^i=\frac{1-q^n}{1-q}\\ [n]!_q=\frac{\prod_{i=1}^n (1-q^i)}{(1-q)^n}\\ \frac{[n]!_q}{[n-m]!_q\times [m]!_q}=\frac{\frac{\prod_{i=1}^n(1-q^i)}{(1-q)^n}}{\frac{\prod_{i=1}^{n-m}(1-q^i)}{(1-q)^{n-m}}\frac{\prod_{i=1}^m(1-q^i)}{(1-q)^m}}=\\ \frac{\prod_{i=1}^n(1-q^i)}{(\prod_{i=1}^{n-m}(1-q^i))(\prod_{i=1}^m(1-q^i))}=\frac{\prod_{i=n-m+1}^n (1-q^i)}{\prod_{i=1}^m (1-q^i)} \]

那么就可以记为

\[\begin{bmatrix}n\\m \end{bmatrix}_q=\frac{[n]!_q}{[n-m]!_q\times [m]!_q}\tag4 \]

这个东西和组合数非常像，因此很好记。

然后证明一下开始那个公式，用数学归纳法。

如果 \(m=1\)，根据其意义可以简单得到方格个数显然 \([1,n]\) 中各一种，因此答案就是 \(\sum_{i=0}^n p^i=\frac{ (1-q^n)}{1-q}\)，得证。

剩下的情况就是暴力展开，先咕着。

part 2 q-Binomial 定理

可以发现上面那个式子和组合数很像，那么就考虑一个类似的二项式定理。

回忆一下二项式定理：

\[(x+y)^n = \sum_{i=0}^n \binom{n}{m}x^iy^{n-i} \]

本质上是枚举 \(x\) 选了几个。

这个定理是

\[\prod_{i=1}^n(y+q^ix)=\sum_{i=0}^n q^{i(i+1)/2}\begin{bmatrix}n\\i \end{bmatrix}_qy^{n-i}x^i\tag5 \]

考虑还是枚举 \(x\) 选了几个，那么相等于 \(a_i=q^i\) 这个序列里面选一个子序列乘起来，问题就和前面的组合意义差不多了，但是要保证 \(b_i\) 互不相等。

这个东西可以考虑先去算 \(b_j-j\)，这个东西可以一样，然后再加回去自然就是两两不同了。

那么考虑就是长度为 \(i\) 的序列，取值为 \([1,n-i]\) 单调不降的序列个数，这个显然就是 \(\begin{bmatrix}(n-i)+i\\i \end{bmatrix}_q\)，那么每个 \(b_j\) 都去加 \(j\)，总共个数就是 \(i(i+1)/2\)，因此可以得到上面的式子。

接下来考虑范德蒙德卷积

\[\sum_{i=0}^n\binom{n}{i}\binom{m}{n-i}=\binom{n+m}{n}\\ \sum_{i=0}^n \binom{n}{i}^2 =\binom{2n}{n} \]

下面那个是带入 \(n=m\) 的结果。

本质上是枚举 \(n\) 个里面选几个，剩下的到 \(m\) 里面去选。

类似的，考虑 \(\begin{bmatrix}n+m\\m \end{bmatrix}_q\) ，那么考虑前 \(n\) 步向右走了几格，就可以得到

\[\sum_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}_q\begin{bmatrix}m\\n-i \end{bmatrix}_q \]

但这样左上角有一部分需要乘上，如图：

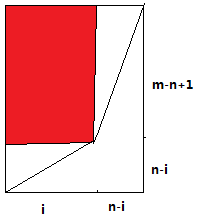
红色部分就没有算上，需要乘上，所以

\[\sum_{i=0}^nq^{i(m-n+i)}\begin{bmatrix}n\\i \end{bmatrix}_q\begin{bmatrix}m\\n-i \end{bmatrix}_q\tag6=\begin{bmatrix}n+m\\n \end{bmatrix}_q \]

带入 \(n=m\)，可以得到

\[\sum_{i=0}^nq^{i^2}\begin{bmatrix}n\\i \end{bmatrix}_q^2=\begin{bmatrix}2n\\n \end{bmatrix}_q\tag7 \]

考虑组合数有个很有用的上指标求和公式：

\[\sum_{i=k}^n \binom{i}{k}=\binom{n+1}{k+1} \]

类似的，可以考虑展开递推式子，可以得到

\[\sum_{i=k}^n \begin{bmatrix}i\\k \end{bmatrix}_q q^i= \begin{bmatrix}n+1\\k+1 \end{bmatrix}_q\tag8 \]

part3 q-Binomial 级数

可以先阅读 普通生成函数

考虑

\[(\frac{1}{1-x})^n=\sum \binom{n-1+k}{k}x^k \]

类似的，考虑这样一个式子

\[\prod_{i=0}^n (\frac{1}{1-q^ix}) \]

那么 \(\frac{1}{1-q^ix}=\sum_{}q^{ij}x^j\)，可以这样理解，就是说有 \(n\) 堆石子，每堆石子有无限个，在第 \(i\) 堆里选 \(1\) 个会产生 \(q^i\) 的贡献，求选 \(k\) 个石子的总贡献。

那么这个就和之前的组合意义很像了，就是相当于对于所有序列 \(b\) 表示选了的堆，那么答案就是 \(\sum \prod q^{b_i}\)，容易得到答案是

\[\prod_{i=0}^n (\frac{1}{1-q^ix})=\sum \begin{bmatrix}n+k\\k \end{bmatrix}_q x^k\tag9 \]

---

CF1603F

给定三个正整数 \(n, k, x\)，求满足以下条件的序列 \(a_{1...n}\) 的个数：

• 对于每一个 \(1 \leqslant i \leqslant n\)，\(0 \leqslant a_i < 2^k\)。
• 序列 \(a\) 没有异或和为 \(x\) 的非空子序列。

对于每一组数据，\(1 \leqslant n \leqslant 10^9, 0 \leqslant k \leqslant 10^7, \sum k \leqslant 5 \times 10^7, 0 \leqslant x < 2^{\min(20, k)}\)。 答案对 \(998\ 244\ 353\) 取模。

相当于把 \(n\) 个数扔到线性基里去。

考虑如果 \(x=0\)，那么相当于所有数都放了进去。

如果 \(x\ne 0\)，那么所有 \(x\) 的方案显然都相同，考虑如果线性基里有 \(m\) 个数了，那么会产生 \(2^{m}-1\) 的贡献。

那么只需要算放入 \(m\) 个数的方案数即可。

考虑先放 \(m\) 个数，然后剩下的插入。那么一开始放入的方案数就是 \(\prod_{i=0}^{m-1}(2^k-2^i)\)。

考虑如果一个一个插入就会有顺序的问题，因此考虑每个空位插几个然后卷起来。

容易得到答案是 \([x^{n-m}]\prod_{i=0}^m \frac{1}{1-2^ix}=\begin{bmatrix}n\\m \end{bmatrix}_2\)。

code

---