各种卷积总结
卷疯了。
前置
卷积,就是解决下面的问题:
已知两个序列 \(f,g\),求一个序列 \(h\),满足
\[h_x=\sum_{i\oplus j=x} f_ig_j \]这里 \(\oplus\) 表示一种运算,一般用这个运算来区别各种卷积。
这个卷积一般暴力都是 \(O(n^2)\) 的,下面主要的就是一些优化这个复杂度的卷积类型。
max 卷积
最简单的卷积。
考虑怎么样的 \(f(i)\) 可能会对 \(h(x)\) 产生贡献,显然是 \(i\le x\) 的,那么可以考虑容斥一下,先求出一个 \(h\) 的前缀和然后再还原。
这个前缀和很好求,因为就是
假设对 \(f\) 求前缀和之后得到的东西是 \(f'\),那么
这个变换就是前缀和,然后还原也很简单,复杂度 \(O(n)\)。
这种变换后直接乘,然后再还原是一种很重要的思想。
来个题
题比较长,自己看吧。
可以注意到 \((1,1,1...1)\) 走到 \((x_1,x_2...x_n)\) 需要满足在 \(n\) 个图中都存在一条长度为 \(s\) 的,\(1\) 到 \(x_i\) 的路径。
由于是无向图,所以一个走到了可以一直在一条边上反复横跳,这样就可以发信是否走到只与奇偶性有关。
所以对于每张图每个点跑一个奇数最短路和一个偶数最短路,那么答案就是。
这个比较难搞,一个变换是 \(a+b=\min(a,b)+\max(a,b)\),移一下项,变成:
三者等价,分别计算。
考虑如果只有两个图,\(A(x)\) 表示 \(A\) 中路径长为 \(x\) 的点数,\(B(x)\) 表示另一个,那么合并就是 \(\max\) 卷积了。
位运算卷积(FWT)
多项式加法卷积(快速傅里叶、数论变换)
要来了。
也就是我们一般认识的多项式乘法。
首先把对于一个多项式而言,如果我们其最高次项为 \(n\) 次,那么确定 \(n+1\) 个点值也就可以确定这个多项式。
点值有什么好处呢?因为如果已知 \(f(x)\) 和 \(g(x)\),那么 \(h(x)=f(x)g(x)\)
而快速傅里叶变换就可以把求点值,点值转换为多项式的部分变成 \(O(n\log n)\)。
首先引入一个单位根。
单位根就是一类复数,用 \(\omega_n\) 表示,且满足 \((\omega_n) ^n=1,\omega_n=e^{\frac{2\pi i}{n}}\)。
这个东西有啥性质呢,就是放在坐标轴上,\(e^{\theta i}=\cos(\theta)+i(\sin(\theta))\),也就是相当于 \(\omega_n\) 表示把单位圆分成 \(n\) 份,取其中的一份,并且容易发现 \(\omega_n^k\) 就相当于取其中的 \(k\) 份。
然后来求解 \(n-1\) 次多项式的点值,把 \(\omega_n^k,k\in[0,n-1]\) 带入,这里需要保证 \(n\) 是 \(2\) 的幂次的形式,如果不是,那就需要用 \(0\) 补上。
把它按次数的奇偶性拆成两个多项式
此时把单位根带进去。
由于刚才的几何意义,所以 \(\omega_n^k=\omega_{dn}^{dk}\)
考虑右边的东西,如果 \(k<\frac{n}{2}\),那么可以直接除 \(2\),变成
如果 \(k>\frac{n}{2}\),那么写成 \(\frac{n}{2}+k\),注意到 \(\omega_n^{\frac{n}{2}}=-1\)。
以上两种情况都把原来的 \(n-1\) 次多项式减半,且 \(k\) 的取值范围也减半,这显然可以分治成两个部分求解,然后合并即可,然后就可以用递归写。
复数建议自己写,不要用 STL 的。
这个求点值的变换叫做 dft。
但还要转化回来,咋做呢,证明比较困难,只需要记个结论好了,就是只需要把单位根的复数部分乘个 \(-1\) 即可。
这是递归版本的。
#include<bits/stdc++.h>
using namespace std;
const int N=3E6+5;
const double Pi=acos(-1);
struct Cp{
double x,y;/*实部,虚部*/
inline Cp(double x=0,double y=0):x(x),y(y){}
}f[N<<1],t[N<<1],g[N<<1];
Cp operator +(const Cp &x,const Cp &y){return Cp(x.x+y.x,x.y+y.y);}
Cp operator -(const Cp &x,const Cp &y){return Cp(x.x-y.x,x.y-y.y);}
Cp operator *(const Cp &x,const Cp &y){return Cp(x.x*y.x-x.y*y.y,x.x*y.y+x.y*y.x);}
Cp operator /(const Cp &x,const Cp &y){// 除法没有用
double di=y.x*y.x+y.y*y.y;
return Cp((x.x*y.x+x.y*y.y)/di,(y.x*x.y-x.x*y.y)/di);
}
void dft(Cp *f,int len,double T){
if(len==1)return;
int mid=len>>1;
Cp *fl=f,*fr=f+mid;
for(int i=0;i<len;i++)t[i]=f[i];
for(int i=0;i<mid;i++)fl[i]=t[i<<1],fr[i]=t[(i<<1)|1];
dft(fl,mid,T);
dft(fr,mid,T);
Cp w1=Cp(cos(2*Pi/(len*1.0)),T*sin(2*Pi/(len*1.0))),now=Cp(1,0);
for(int i=0;i<mid;i++,now=now*w1){
Cp tot=now*fr[i];//这个地方叫做蝴蝶变换,就是一下子对左右都进行计算,减小常数
t[i]=fl[i]+tot;
t[i+mid]=fl[i]-tot;
}
for(int i=0;i<len;i++)f[i]=t[i];
}
int n,m;
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++)scanf("%lf",&f[i].x);
for(int i=0;i<=m;i++)scanf("%lf",&g[i].x);
n+=m;
for(m=1;m<=n;m<<=1);
dft(f,m,1.0);
dft(g,m,1.0);
for(int i=0;i<m;i++)f[i]=f[i]*g[i];
dft(f,m,-1.0);
for(int i=0;i<=n;i++)printf("%d ",(int)(f[i].x/m+0.49999));
}
递归常数大,还是要用递推写法。
考虑这个不断左右分治的过程是怎么样的,给个图。
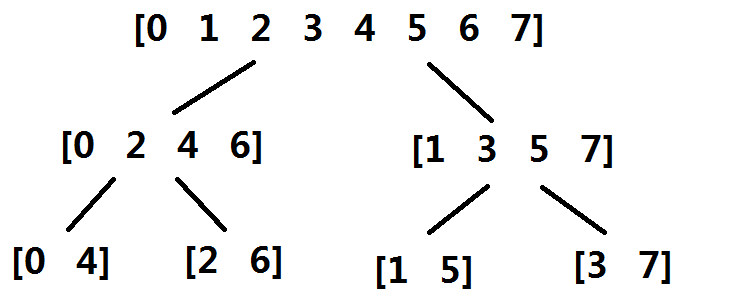
也就是说,我们只需要求出 0 4 2 6 1 5 3 7 这个序列,这样每次把相邻两个合并做一遍即可。
但这个序列怎么求呢?当然可以递归求。
考虑把这个序列的二进制形式写出来
000 100 010 110 001 101 011 111
可以发现,就是把每个数字的二进制为取反了。
实现也很好写,直接递推即可。
得到最后的代码
const int N=4e5+5;
const double Pi=acos(-1);
struct Cp{double x,y;};
Cp operator+(Cp a,Cp b){return (Cp){a.x+b.x,a.y+b.y};}
Cp operator-(Cp a,Cp b){return (Cp){a.x-b.x,a.y-b.y};}
Cp operator*(Cp a,Cp b){return (Cp){a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
int cnt[N],S,l;
void FFT(Cp *A,int T){
for(int i=0;i<=S;i++)if(i<cnt[i])swap(A[i],A[cnt[i]]);
for(int len=1;len<S;len<<=1){
Cp W=(Cp){cos(Pi/len),T*sin(Pi/len)};
for(int L=0;L<S;L+=(2*len)){
Cp now=(Cp){1,0};
for(int k=0;k<len;k++,now=now*W){
Cp x=A[L+k],y=A[L+len+k]*now;
A[L+k]=x+y,A[L+len+k]=x-y;
}
}
}
}
Cp A[N],B[N];
void mul(double *a,double *b,double *ans,int n,int m){
for(S=1,l=0;S<=n+m;S<<=1,l++);
for(int i=0;i<=S;i++)A[i].x=A[i].y=B[i].x=B[i].y=0;
for(int i=0;i<=n;i++)A[i].x=a[i];
for(int i=0;i<=m;i++)B[i].x=b[i];
for(int i=1;i<=S;i++)cnt[i]=(cnt[i>>1]>>1)+((i&1)<<(l-1));
FFT(A,1),FFT(B,1);
for(int i=0;i<=S;i++)A[i]=A[i]*B[i];
FFT(A,-1);
for(int i=0;i<=S;i++)ans[i]=A[i].x/S;
}
FFT 是用复数实现的,会有一定的精度问题,而且常数依然很大。
能不能用整数实现?这就是 NTT。
可以发现,在模 \(p\) 意义下,\(\omega_n=g^{\frac{p-1}{n}}\),可以用上面推的相关结论证明,这里 \(g\) 是原根。
因此直接换一个单位根就好了,注意这里的 \(p\) 需要满足是 \(a2^k+1\) 的形式,这里 \(2^k\) 要大于 \(n\),模数一般是 \(998244353\),其原根是 \(3\)。
更多高级技巧以及应用:link
狄利克雷卷积(乘法卷积)
这个东西直接做就是调和级数 \(O(n\log n)\) 的,只能跑 \(10^6\) 级别的。
- 一个函数是积性函数
先考虑一个简单的。
也就是 \(g_i=1\),此时满足
这个东西像是一个高维前缀和,把每个质数看成是一维,然后直接来就好了,复杂度和埃氏筛一样 \(O(n\log \log n)\)
for(int i=1;i<=cnt;i++)for(int j=p[i];j<=n;j+=p[i])a[j]+=a[j/p[i]];
然后考虑把 \(g\) 换一下,变成 \(\mu\)。
考虑 \(\mu\) 的意义,如果一个 \(j\) 含有平方因子就是 \(0\) 了,因此相当于每个质数在这个前缀和中最多做一次贡献,所以第二维需要倒着枚举。
做一次贡献,也就是乘上一个 \(-1\),因此直接来。
for(int i=1;i<=cnt;i++){
for(int j=n/p[i];j;j--)f[j*p[i]]=(f[j*p[i]]-f[j]+mod)%mod;
}
考虑更加一般的情况,就是 \(g\) 是一个积性函数。
如果是一个完全积性函数,那么直接对于每个质数直接前缀和,然后乘上一个系数即可,复杂度 \(O(n\log \log n)\)。
for(int i=1;i<=cnt;i++)for(int j=p[i];j<=n;j+=p[i])a[j]+=a[j/p[i]]*f[p[i]];
如果不是,那么显然需要去枚举当前选了 \(p^k\)。
复杂度可以等比数列证明一下也是 \(O(n\log \log n)\),常数稍大。
for(int i=1;i<=cnt;i++)for(ll k=p[i];k<=n;k*=p[i])for(int j=k;j<=n;j+=k)a[j]+=a[j/k]*f[k];
- 两个都是积性函数
既然两个函数都是积性函数,那么卷出来的 \(h\) 显然也是积性函数。
因此只需要算出 \(h(p^k)\) 就可以了欧拉筛 \(O(n)\) 做了。
考虑对于 \(h(p^k)\) 直接暴力 \(O(k)\) 做。
这个是 \(O(n)\) 的,证明在 这里
快速幂
已知一个多项式 \(A(x)\),求 \((A(x))^k\),这里乘法是上面卷积的一种。
有一种很简单粗暴的做法就是直接和快速幂一样做,复杂度就是乘上一个 \(O(\log k)\),这里介绍一个另外的做法。
考虑除了迪利克雷卷积之外,其他卷积都是先求点值,点乘然后再加回去。
那么求出点值,然后直接快速幂算出点值的 \(k\) 次方,再还原即可。
但是注意多项式卷积不能这样,因为两个长度为 \(n\) 的多项式会卷成一个 \(2n\) 的,长度会变,换言之,一次卷积后把 \(>n\) 次项去掉后再变换和原来的多项式不相等了,因为一个长度为 \(2n\) 的多项式无法用 \(n\) 个点值来表示,因此要先把长度开到 \(nk\),复杂度是 \(O(nk\log k)\),比较逊但是很好写。
高维卷积
就是有 \(k\) 维,每一维做一个运算卷起来。
没啥好说的,就是每一维分开做就好了,例如对于二维卷积,先枚举每一行,对每行做一次,然后枚举每一列,做一次即可。
ABC265Ex \(\color{Gold}\bigstar\)
有 \(n\times m\) 列的矩阵,有两个人博弈,每行放有一黑一白两个棋子,两人轮流操作,先手每次选择一个黑子向右移动至少一格距离,后手每次选择一个白子向左移动至少一格距离,棋子遇到其他棋子或者遇到边界就要停下,无法操作者输,求有多少种放子方案满足先手可以获胜,答案对 \(998244353\) 取模。
\(n\le 8000,m\le 30\)。
显然行与行之间互不干扰。考虑一行,如果黑在左,白在右,那么显然就是一个简单的 nim,否则显然每次操作只移动一次最优,因此就是相当于左右比大小。
赛时比较降智,可以把两个分开做然后合并一下,暴力复杂度 \(O(n^2m)\),但是时限 10s,但是还是没调出来。
实际上令 \(f_{i,j}\) 表示一种状态 sg 值为 \(i\),左边比右边多 \(j\) 的方案数,那么答案就是 \(f^n\) 然后去统计即可。
这个东西简单快速幂即可。
ABC212Ex *2741 \(\color{green}\bigstar\)
有 \(k\) 个数,可以选择最多 \(n\) 个数,一个数可以被重复选,这样会有 \(\sum_{i=1}^n k^i\) 种方法,每种方法,选的一个数 \(x\) 对应有一堆大小为 \(x\) 的式子,然后进行 nim 游戏,求先手必胜的选数方案数,答案对 \(998244353\) 取模。
\(n\le 2\times 10^5,k,a_i< 2^{16}\)。
第一个 Ex,梦开始的地方,不过不是很难。
考虑相当于选若干个数满足异或和为零,一个简单的思路是开一个桶然后直接异或卷积即可。
假设桶是 \(F\),那么就是 \(\sum_{i=1}^n F^i\),可以等比数列求,更简单的方法是 DFT 后算等比数列然后再 IDFT。

