【典】CF713C 堆维护凸壳优化dp
其实是一个五倍经验题:
CF713C *2300
CF13C *2200
有一个长度为 \(n\) 的序列 \(a\),求一个非递减序列 \(b\) ,使得 \(\sum_{i=1}^n |a_i-b_i|\)。
\(n\le 10^6,a_i\le 10^9\)。
part 1 \(O(n^2)\)
数据范围最小的是两个 CF 题,\(O(n^2)\) 都可以过。
考虑一个简单的 dp,\(f_{i,j}\) 表示前 \(i\) 个数,第 \(i\) 个数选 \(j\) 的最小值。
维护前缀最小值就可以得到 \(O(na_i)\) 的做法。
但是可以发现一个显然的性质,最后得到的 \(b\) 中的数一定都在 \(a\) 中出现过,否则可以通过简单的调整法,也就是对于排序后的一个区间 \((a'_i,a'_{i+1})\) 中间有数在 \(b\) 里,那么可以一个前缀变成 \(a'_i\),后缀变成 \(a'_{i+1}\) 即可。
所以直接离散化就可以优化到 \(O(n^2)\)。
part 2 \(O(n\log n)\) 可并堆
考虑这样一个问题,如果把一堆数变成一个数,要求绝对值和最小咋做。
经典结论直接中位数即可。
那么考虑最后的 \(b\) 一定可以看成是若干个区间,每个区间都是对应 \(a\) 的中位数最优。
但是可能不满足不递减。
所以用可并堆维护,如果后面的中位数比前面小就合并。
每次加一个数,这个数单独成堆,然后不断与前面合并即可。
part3 \(O(n\log n)\) 堆+斜率
最强的一个做法,主要是因为好写。
依然考虑上面的 dp 做法,我们改一下,改成另 \(f_{i,j}\) 表示 \(a_i\le j\) 的最优解。
那么状态也很好搞:
然后我们把 \(f_i\) 的图像画出来,可以发现每次这个图像是加上一个绝对值函数然后再取一个后缀 \(\min\)。
最后的答案相当于就是最下面的拐点。
下面来维护一下这个过程。

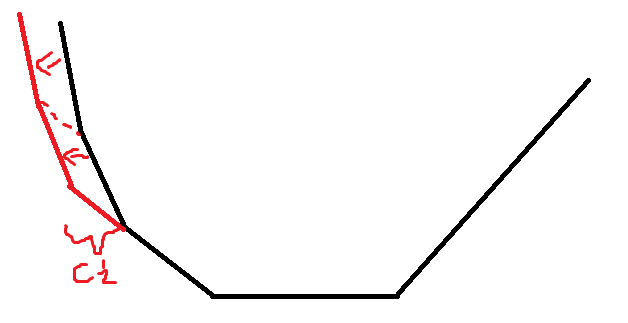
这是最开始 \(f_1\) 的图形,拐点就是 \(a_1\)。
然后我们在右边加一个点(\(a_2>a_1\))。
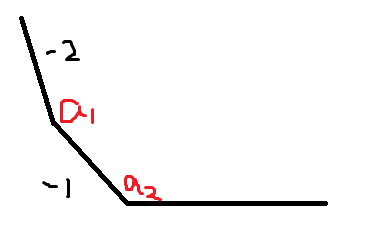
可以发现,左边的斜率全部减一,但此时答案不变。
因此,如果一直在右边加点,会形成一个这样的图形:

也就是一个凸壳。
接下来考虑在左边加上一个点。
可以发现就是右边所有线段的斜率加一,右边斜率全部减一。
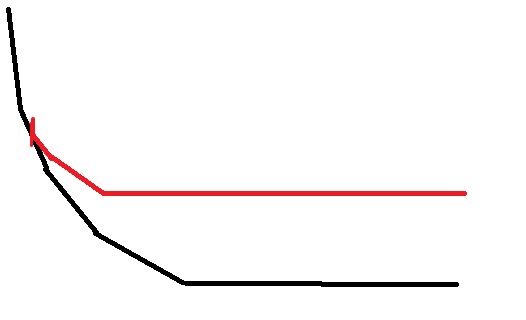
那么对答案的贡献就是下面黑线和上面红线之间的距离。
可以发现就是最下面拐点的坐标与 \(a_i\) 的差,维护拐点的话就相当于删掉最后面一个。
考虑一个拐点本质上就是使得左边斜率是右边斜率减一,因此直接用一个堆维护即可。
上面的情况直接加入这个拐点,下面的情况就把最大值弹了。
考虑方案怎么构造。
可以发现发现每次只需要让 \(a_i\) 等于最优的拐点即可,也就是堆顶,但是这个可能会被后面的更新,所以取后缀最小值即可。
P8476 \(\color{blue}\bigstar\)
给定非负整数序列 \(\{a_n\}\),定义函数 \(f(x,y)\) 为
\[f(x,y)=\begin{cases} x-y,&x\ge y\\ C,&x< y \end{cases}, \]其中 \(C\) 是给定常数。请构造一个不增非负整数序列 \(\{b_n\}\),最小化
\[\sum_{i=1}^nf(b_i,a_i). \]你仅需输出这一最小化的结果。
\(n\le 10^6,a_i\le 10^9\)。
做法类似,考虑 \(f\) 的图像就是前面一段是 \(C\) 后面是一个斜率为 \(1\) 的直线,每次加上这个图像之后后缀取 \(\min\)。
考虑对于一个 \(a_i\),右边的变化就是所有线的斜率加一,前面就相当于全部加 \(C\),然后和 \(a_i\) 的值取 \(\min\)。
可以发现这个取 \(\min\) 不能用堆维护,那么用线段树维护离散化后的点值,前缀就可以直接加然后暴力取 \(\min\),后缀就直接加的就是离 \(a_i\) 的距离,因此可以先加 \(a_j\) 然后区间减 \(a_i\)。
比较阿拉丁,还好一次过了。
P3642 \(\color{blue}\bigstar\)
给一棵树,边有边权,每次操作可以把一条边加一或者减一,需要满足边权非负,求让所有叶子深度相同所需要的最少操作次数。
\(n\le 3\times 10^5\)。
开始有一个憨憨想法,就是直接算出每个点的深度,然后直接 dp,但这个有一个问题,就是权值需要非负。
考虑设 \(f_{i,j}\) 表示 \(i\) 子树内点的深度为 \(j\) 的答案。
考虑向上面转移,假设边权是 \(c_i\) ,显然先向右边平移 \(c_i\) 个单位,
然后下一步就是一个点对左右两边的贡献,那么这个贡献就是一个绝对值函数。
长这样。
然后考虑整体函数的移动是怎么样的,\(l\) 的右边整体右移 \(c_i\),\([l,l+c_i]\) 是一个斜率为 \(-1\) 的东西,左边的相当于向上平移了 \(c_i\)。
考虑用堆维护,维护拐点即可。
合并多个,考虑两个函数相加,一段的斜率就是两个加起来,那么合并之后把最大值弹掉就可以维护右边是斜率为 \(1\) 的结构了。
至于答案,考虑 \(0\) 处的答案是边权之和,然后可以轻松求出了。
ABC217Ex *3112 \(\color{blue}\bigstar\)
有一个人开始在 \(0\) 处,每个时刻可以向左走一格或者向右走一格,有 \(n\) 次攻击,时间为 \(t_i\),位置是 \(x_i\),攻击有两种,当前位置为 \(p\),一种伤害为 \(\max(0,p-x_i)\),另一种是 \(\max(0,x_i-p)\)。
求最少受到的伤害。
\(n\le 2\times 10^5\)。
不是很难。
考虑一个时间间隔 \(t_i-t_{i-1}\) 就是一个点向左右去更新,如果最小值区间为 \([l,r]\),那么就分别 \(l\) 左移,\(r\) 右移时间长度即可。
加一个函数就分在区间左边还是右边即可。
具体的,开两个堆维护 \([l,r]\) 左边和右边的拐点,平移不太好维护,那么就对于右边的维护 \(x-t\),左边维护 \(x+t\) 即可,这样需要用的时候在算上 \(t\) 即可。
注意特判 \(x\) 这个地方走不到对答案的贡献。