多项式计数

前置知识

• 多项式乘法（FFT，NTT）

• 普通生成函数

• 一些简单的计数，dp 技巧（？

附：我的多项式乘法板子。

模拟赛如果找不到题出，可以直接把下面随便一个题的 \(n\) 改成 \(5000\) 就可以了。

让我们开始吧！

多项式乘法计数

千里之行，始于足下。

这一块不需要任何多项式全家桶内容，只需要最简单的 FFT，NTT 便可完成。

NTT 的卷积形式是：

\[f(x)=A*B=\sum_{i=0}^x A(i)B(x-i) \]

所以只要把式子尽量变成这样就好了，一般来说组合数都很适合卷积，如果出现 \(n-i\) 这样的东西可以翻转一下变成 \(i\)，然后推出上面的形式。

---

P3338 \(\color{green}\bigstar\)

已知长度为 \(n\) 的序列 \(q\)，对于每个 \(1\le j\le n\)，求：

\[F_j=\sum_{i = 1}^{j - 1} \frac{q_i}{(i - j)^2}-\sum_{i = j + 1}^{n} \frac{q_i}{(i - j)^2} \]

\(n\le 10^5\)。

简单推式子题，显然左右本质相同，只需要倒过来再求一遍就好了，所以考虑左边的东西咋算，换成枚举 \(i-j\) 就好了。

\[\sum_{i = 1}^{j - 1} \frac{q_i}{(i - j)^2}=\sum_{i = 1}^{j - 1} \frac{q_{j-i}}{i^2}=\sum_{i = 1}^{j - 1} q_{j-i}g_{i} \]

这里 \(g_i=\dfrac{1}{i^2}\)。

显然是一个卷积了，直接求就好了。

code

---

P5641 \(\color{green}\bigstar\)

已知一个长度为 \(n\) 的序列 \(a\) 和一个数 \(k\)，定义

\[sum_{k,l,r}=\begin{cases}\sum\limits_{i=l}^{r}a_i&,k=1\\\sum\limits_{i=l}^{r}\sum\limits_{j=i}^{r}sum_{k-1,i,j}&,k\geq 2\end{cases} \]

求对于所有 \(1\le j\le n\)，求 \(sum_{k,1,j}\)。
\(n\le 10^5\)。

简单题，考虑每个 \(a_i\) 对答案的贡献，可以发现本质上是一个区间每次可以左边扩充几个位置，右边扩充几个位置，最后扩充成 \([1,j]\) 的方案数。

可以用插板法直接得到式子：

\[sum_{k,1,j}=\sum_{i=1}^j a_i\binom{i-1+k-1}{k-1}\binom{j-i+k-1}{k-1} \]

定义 \(g_{i}=\binom{i+k-1}{k-1}\)，注意 \(k\) 很大，所以只能递推计算。

\[sum_{k,1,j}=\sum_{i=1}^j ((a_ig_{i-1})g_{j-i}) \]

显然卷积形式，左边两个先乘起来再和右边卷就好了。

---

AGC005F *3440 \(\color{blue}\bigstar\)

给定一棵无根树，定义 \(f(k)\) 表示对于所有大小为 \(k\) 的点集，求出能够包含它的最小连通块大小之和。对于 \(1\le k\le n\) 的所有 \(k\)，求出 \(f(k)\)。
\(n\le 2\times 10^5\)。

人生第一次自己做出 AGC F 祭，题不难，但我想了好久。

其实不是很难，考虑每个点对答案的贡献，如果一个点 \(i\) 会在点集 \(S\) 对应的联通块里，需要满足以下两个条件之一：

• \(i\in S\)。

• \(i\) 至少有两个子树中含有 \(j\)，满足 \(j\in S\)。

考虑如果是第一种情况，那么答案就是 \(\binom{n}{k}\times k\)。

如果不满足第一种情况但满足第二种情况，把至少两个改成总数减去只有一个，那么总数就是 \(\binom{n-1}{k}\times n\)。

然后考虑只有一个子树的情况。

答案显然是

\[\sum_{u=1}^n \sum_{(u,v)} \binom{siz_v}{k} \]

此处 \(siz_v\) 是指以 \(u\) 为根时的子树大小。

然后可以发现子树大小不超过 \(n\)，所以可以换成这样：

\[\sum_{i=1}^n c_i\binom{i}{k} \]

\(c_i\) 表示大小为 \(i\) 的子树数量。

然后就简单了，直接推。

\[\sum_{i=1}^n c_i\binom{i}{k}=\frac{1}{k!}\sum_{i=1}^n c_i\frac{i!}{(i-k)!} \]

令 \(f_i=c_ii!,g_i=\frac{1}{i!}\)，那么变成

\[\frac{1}{k!}\sum_{i=1}^n f_ig_{i-k} \]

显然把 \(g\) 倒过来就可以直接卷积了，然后直接做完了。

注意这题模数是 \(924844033\)，这是 NTT 模数，原根是 \(5\)。

code

---

CF827E *2700 \(\color{Gold}\bigstar\)

有一个长度为 \(n\) 的字符串 \(S\)，只含有 V,K,?，可以把 ? 换成 V,K，求所有可能的周期长度。
\(n\le 5\times 10^5\)。

假设一个周期长度为 \(x\) ，那么就相当于 \(S_{1...n-x+1}=S_{x+1...n}\)，变成了一个字符串匹配问题。

如果没有 ?，显然可以用 hash 解决，但有通配符。

考虑使用多项式，假设一个位置匹配是 \(0\)，不匹配是 \(>0\)，那么如果没有 ?，可以令。

\[f(x)=\sum_{i=1}^{n-x+1}(s(i)-s(i+x))^2 \]

其中 \(S(i)=V\) 则 \(s(i)=1\)，否则 \(s(i)=2\)。

然后考虑通配符相当于直接把一个值变成 \(0\)，那么令通配符所在位置 \(s(i)=0\)，那么：

\[f(x)=\sum_{i=1}^{n-x+1}(s(i)-s(i+x))^2s(i)s(i+x) \]

考虑这东西咋算，考虑令 \(t(i)=s(n-i+1)\)，即翻转一下，这样变成：

\[f(x)=\sum_{i=1}^{n-x+1}(s(i)-t(n-i-x+1))^2s(i)t(n-i-x+1)\\ =(\sum_{i=1}^{n-x+1}s(i)^3t(n-i-x+1))+(\sum_{i=1}^{n-x+1}s(i)t(n-i-x+1)^3)+(\sum_{i=1}^{n-x+1}s(i)^2t(n-i-x+1)^2) \]

这显然是一个卷积，直接 NTT 计算即可。

然后你会发现寄了，第一个样例输出：

3
2 3 5

为啥会多一个 \(2\) ？

观察可以发现，第 \(3\) 个位置的 ? 既和第一个位置的 V 匹配，又和最后一个 K 匹配，但是通配符只能变成其中一个，所以 \(2\) 不是周期。

由于一个串自己和自己匹配，所以可以拿一张经典图：

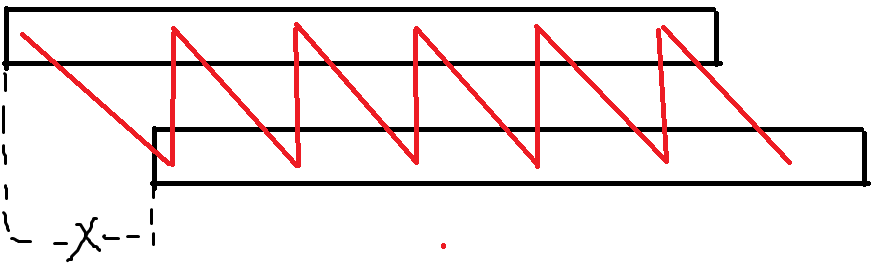
图中红线位置需要相等。

也就是如果一个 \(x\) 是答案，需要满足 \(S_i=S_{i+x}=S_{i+2x}=S_{i+3x}...\)，而在上面我们只判断了 \(S_i=S_{i+x}\)。

所以可以调和级数暴力判断，时间复杂度 \(O(n\log n)\)，需要一定的卡常。

code

如果卡常遇到困难，可以看常数优秀的 做法，因为原串中只有两个字符，只需要你进行两次卷积，大大减少常数。

类似的题：P4173，P4199。

---

P5075 \(\color{green}\bigstar\)

有 \(m\) 颗糖，有 \(n\) 个人排成一排，你需要把糖分给这些人，使得没有分到糖的人是一个后缀，每个人的快乐度是 \(f(x)\)，\(x\) 表示获得的糖数，\(f(x)=Ox^2+Sx+U\)，其中 \(O,S,U\) 是给定的三个常数，特别的，\(f(0)=1\)。
一种分配方案的权值是所有人快乐度的乘积，求所有合法方案权值的乘积，答案对 \(P\) 取模。
\(m\le 10000,n\le 10^8,P\le 255\)。

首先，\(n\) 的取值范围是假的，因为最多只有一个长度为 \(m\) 的前缀中的人可以分到糖。（虽然没啥用。

先考虑一个简单的 dp，设 \(g_{i,j}\) 表示前 \(i\) 个人分 \(j\) 棵糖的权值之和。

\[g_{i,j}=\sum_{k=1}^{j} g_{i-1,j-k}\times f(k) \]

可以发现显然是一个卷积形式，只不过把 \(f(0)\) 扣掉了，所以把第二维压掉，变成：

\[g_i=g_{i-1}*(f-1)=(f-1)^i \]

由于可以在任意一个地方停止，所以答案就是：

\[[x^m] \sum_{i=1}^n (f-1)^i \]

可以用等比数列，但是很阿拉丁，因为需要多项式求逆，但是我不会。

等比数列求和有一个知名的做法：

\[\sum_{i=1}^{2n} (f-1)^i=((f-1)^n+1)\sum_{i=1}^n (f-1)^i \]

所以可以记录一下 \(\sum_{i=1}^n (f-1)^i\) 和 \((f-1)^n\)，然后就可以分奇偶性递归求解了，总时间复杂度 \(m\log^2 m\)。

出题人很阴间，模数不是 NTT 模数，需要 MTT。

但也可以不用，可以直接 FFT，模数较小，精度不容易被卡。

注意 FFT 卡精度的方法是 (int)(A[i].x/S+0.5)%mod，而不是 (int)((A[i].x+0.49999)/S)%mod。

code

upd：了转反，由于多项式只有 \(m\) 项，所以一次卷积答案最多只有 \(m^2\times P<998244353\)，所以可以直接 NTT 完了再取模。

---

P4091 \(\color{green}\bigstar\)

已知 \(n\)，求

\[\sum_{i=0}^n \sum_{j=0}^i \begin{Bmatrix}i\\j\end{Bmatrix} \times 2^j\times (j!) \]

\(n\le 10^5\)

考虑先把第二类斯特林数展开，不会的看 这里，并把 \(j\) 的上标换成 \(n\)，这样结果不变。

\[\sum_{i=0}^n \sum_{j=0}^i \begin{Bmatrix}i\\j\end{Bmatrix} \times 2^j\times (j!)=\sum_{i=0}^n \sum_{j=0}^n 2^j\times (j!)\times \frac{1}{j!} \sum_{k=0}^j k^i \binom{j}{k}(-1)^{j-k} \]

可以发现 \(i\) 是作用最小的，所以可以改变枚举顺序。

\[\sum_{j=0}^n 2^j\sum_{k=0}^j \binom{j}{k}(-1)^{j-k}\sum_{i=0}^n k^i\\ =\sum_{j=0}^n 2^j\times j!\sum_{k=0}^j \frac{1}{k!(j-k)!}(-1)^{j-k}\frac{k^{n+1}-1}{k-1}\\ =\sum_{j=0}^n 2^j\times j!\sum_{k=0}^j \frac{(-1)^{j-k}}{(j-k)!}\frac{k^{n+1}-1}{(k-1)k!} \]

显然是卷积形式了，后面两个卷起来然后加起来就好了，注意特判 \(k=0,1\) 的情况，将 \(n=0\) 带入，可以发现当 \(k=0\) 时，右边的值应该是 \(1\)。

code

---

P3321 \(\color{green}\bigstar\)

给出 \(n,m,x\) 和一个集合 \(S\)，求有多少个长度为 \(n\) 的序列 \(a\) 满足 \(a_i\in S\)，且

\[\prod_{i=1}^n a_i \bmod m=x \]

\(m\) 是质数，\(m\le 8000\)，\(n\le 10^9\)。

看到乘积取模，想原根。

转成原根后相当于和等于 \(x\)。

设 \(F_{i}(x)\) 表示长度为 \(i\)，和为 \(x\) 的方案数，容易得到：

\[F_i=F_{i-1}*G \]

\(G(x)\) 表示 \(S\) 中 \(x\) 出现了多少次，这里 \(*\) 是循环卷积，直接快速幂就做完了。

code

---

P3760 \(\color{green}\bigstar\)

已知一个序列，求所有区间和的异或和。
\(n\le 10^5,\sum a_i\le 10^6\)。

单 \(\log\) 被双 \(\log\) 吊打。

考虑显然先前缀和，然后变成差问题，考虑计算一个差值的方案数。

假设 \(f_i\) 表示 \(i\) 在前缀和中的出现次数。

\[g_x=\sum_{i=1}^{m} f_if_{x+i} \]

\(m\) 表示 \(\sum_{i=1}^n a_i\)。

显然把后面那个倒过来，就可以直接卷积了。

注意最大出现次数可能是 \(10^{10} > 998244353\)，所以需要用更大的模数。

草，__int128 常数过大，全 T 了离谱，只能用 FFT。

了转反，\(998244353\) 过了，\(998244353\) nb！

code

---

？？？\(\color{blue}\bigstar\)（毛营的题，不知道链接）

一个可重集的价值是所有元素的按位与，给一个长度为 \(n\) 的序列，对于每个 \(1\le k\le n\) 求出所有选出 \(k\) 个数的可重集中，价值为 \(0\) 的个数，答案对 \(998244353\) 取模。
\(n\le 2^{19},a_i\le 2^{19}\)。

可以直接容斥一下，设 \(c_i\) 表示有多少个 \(i\in a_j\)。

那么一个 \(k\) 的答案是

\[\sum_{i=0}^{2^{19}} (-1)^{|i|} \binom{c_i}{k} \]

\(|i|\) 表示 \(i\) 二进制为下一的个数。

然后考虑算每个 \(c_i\) 对答案的贡献，记贡献为 \(a_i\)。

\[\sum_{i=0}^n a_i\binom{i}{k}=\frac{1}{k!}\sum_{i=0}^n a_i\frac{i!}{(i-k)!} \]

然后把下面的 \((i-k)!\) 反转一下，直接卷积就好了。

code

---

cc COUNTARI *2587 \(\color{blue}\bigstar\)

已知一个长度为 \(n\) 的序列 \(a\)，求有多少对 \(i,j,k\) 满足 \(a_j-a_i=a_k-a_j\) 且 \(i<j<k\)。

\(n\le 10^5,a_i\le 3\times 10^4\)。

先移项，可以发现 \(2a_j=a_i+a_k\)，右边是个卷积，但是需要满足 \(i<j<k\)，不好做。

一个简单的想法是左边和右边卷，暴力复杂度 \(O(n^2\log n)\)，很垃圾。

但是优点是可以查询多个 \(a_j\)，因此考虑分块，对于块内直接暴力，块外左边卷右边即可。

code

---

任意模数 FFT

P4245

最阿拉丁的一个应用，不知道怎么发明出来的。

求两个多项式卷积，模数为任意数 \(p\)，\(p\le 10^9\)。

这个东西直接 FFT 会掉精度。

考虑两个长度为 \(n\) 的多项式卷积，那么答案的一个位置在不取模下最大为 \(n^2p\le 10^{19}\)。

此时我们选 \(3\) 个 NTT 模数分别做一次卷积，然后 CRT 合并即可，容易发现这样数的范围可以达到 \(10^{27}\)，因此可行。

注意模数不要选 \(2^{32}\) 以上的，因为这样乘法常数大的离谱。

这样需要进行 \(9\) 次 NTT，常数比较大，有少几次的 FFT 做法，可以自己去学。

code

---

分治 FFT

分治 FFT 有两种形式，一种是

\[\prod_{i=1}^n f_i(x) \]

如果每个多项式项数比较小，那么就可以直接分治，变成两个区间分别做，然后再通过一次卷积合并，时间复杂度 \(O(n\log^2 n)\)。

注意这里的运算不一定是卷积，其他运算也可以做，比如

\[\sum_{i=1}^n \frac{f_i(x)}{g_i(x)} \]

如果上下系数比较小，也可以直接分治做，复杂度一样。

比如这个题

CF1613F *2600 \(\color{Gold}\bigstar\)

把一棵 \(n\) 个点的有根树涂 \(n\) 种颜色，使得任意节点颜色不等于其父亲的颜色减一，且每个点涂的颜色互不相同，求方案数对 \(998244353\) 取模的结果。
\(n\le 10^5\)。

考虑容斥，枚举一下有多少对父子不满足关系，显然一个节点最多和一个儿子矛盾，所以把不满足关系的两点连边，可以得到一堆链，排列的方案可以直接阶乘做，考虑选这些关系的方案。

假设枚举了 \(k\) 对关系，那么就相当于每个节点在儿子节点中选一个，设 \(d_i\) 表示 \(i\) 的儿子数，那么相当于求：

\[[x^k]\prod_{i=1}^n (1-d_ix) \]

减是因为乘上了容斥系数，直接分治 FFT 计算即可。

code

---

另一种是P4721。

给定序列 \(g_{1\dots n - 1}\)，求序列 \(f_{0\dots n - 1}\)。
其中 \(f_i=\sum_{j=1}^if_{i-j}g_j\)，边界为 \(f_0=1\)
答案对 \(998244353\) 取模。
\(n\le 10^5\)。

考虑使用 cdq 分治解决，对于一个区间 \([l,r]\)，我们先算出 \([l,mid]\) 的 \(f\) 值，然后再去考虑左边对右边的贡献。

显然就是一个区间卷上 \(g\) 的一个前缀，直接做就好了，时间复杂度 \(O(n\log^2 n)\)。

code

---

P5748 \(\color{green}\bigstar\)

一个有 \(n\) 个元素的集合，将其分为任意个非空子集，求方案数对 \(998244353\) 取模。
\(Q\) 次询问，\(n\le 10^5\)。

如果一次查询可以考虑答案等于第二类斯特林数一行加起来，可以直接 \(O(n\log n)\)，但有多组询问。

设 \(f_i\) 表示 \(i\) 个数的答案，那么可以枚举有多少个数和 \(1\) 在同一个集合，得到 \(O(n^2)\) 式子：

\[f_i=\sum_{j=1}^i \binom{i-1}{j-1} f_{i-j}=\sum_{j=0}^{i-1} \binom{i-1}{j}f_{i-j-1}\\ \frac{f_i}{(i-1)!}=\sum_{j=0}^{i-1}\frac{1}{j!}\frac{f_{i-j-1}}{(i-j-1)!} \]

然后可以直接分治 NTT 算，时间复杂度 \(O(n\log^2 n)\)。

code

upd：看题解才知道是贝尔数模板题，但 \(O(n\log n)\) 做法需要指数生成函数和 \(\exp\)，很显然我不会。

upd：会了， \(O(n\log n)\) 做法在 EGF 博客里。

---

P6694 \(\color{green}\bigstar\)

有一个圆上有 \(n\) 个点，现在连一些边形成一个图，连边不能相交，一条边 \((i,j)\) 产生贡献是 \(a_i\times a_j\)，求所有连边方案的总贡献。

\(n\le 10^5\)。

考虑计算每条边对答案的贡献，显然就是左边的连边方案乘上右边的。

这个东西可以设一个 dp，\(f_i\) 表示一个圆弧上有 \(i\) 个点，且首尾已经连边的方案数。

还需要设一个 \(g_i\) 表示首尾不一定连边的方案数，但是很容易发现 \(g_i=2f_i\)，因为首尾连不连边有两种情况。

然后考虑 \(f\) 的转移。

• 第一个点不连边，那么就是 \(g_{i-1}\)。
• 第一个点连边，考虑连哪个即可。

最后得到转移式子

\[f_i=2f_{i-1}+\sum_{j=2}^{i-1} f_jf_{i-j+1} \]

答案就是

\[\sum_{i<j} a_ia_jf_{j-i+1}f_{n-j+i+1} \]

直接做复杂度 \(O(n^2)\)。

code

上面递推可以直接分治 FFT，下面统计答案考虑每个点对答案的贡献，显然是一个简单卷积即可。

---

二项式反演

这个东西和多项式有紧密联系，所以在这里讲。

没想到自己用了很多次的算法居然有个名字。

考虑如果一些容斥的题，一般答案让我们求 \(g_i\) 表示恰好为 \(i\) 时的答案，但是我们一般容易求的是 \(f_i\) 表示钦定 \(i\) 个（也就是大于等于 \(i\) 个）的答案。

考虑两者的关系，可以发现一种恰好选 \(j\) 个的方案会在钦定 \(i\) 个中贡献 \(\binom{j}{i}\)，也就是在全部的 \(j\) 个里钦定 \(i\) 个。

也就是

\[f_i=\sum_{j=i}^n \binom{j}{i} g_j \]

那么如果已知 \(f\) ，怎么求 \(g\) 呢？

先考虑一个 naive 的做法，就是从大到小做，每次拿 \(f_i\) 减去 \(i<j\) 的 \(g_j\) 的贡献，就可以得到 \(g_i\) 了，一路推下去就好了，也就是

\[g_i=f_i-\sum_{j=i+1}^n \binom{j}{i}g_j \]

时间复杂度 \(O(n^2)\)。

考虑这样一个问题，记 \(p_n=\sum_{i=0}^n (-1)^n \binom{n}{i}=[n==0]\)

证明比较简单，直接二项式定理 \((a+b)^n\) ，带入 \(a=1,b=-1\) 即可。

因此通过这个来消除 \(g\) 对 \(f\) 的贡献，可以得到

\[f_i=\sum_{j=i}^n (-1)^{j-i}\binom{j}{i} g_j \]

得到了一个优美的式子，考虑卷积优化。

先把 \(j\) 变成 \(n-j\)。

\[f_i=\sum_{j=0}^{n-i} (-1)^{n-j+i}\binom{n-j}{i} g_{n-j} \]

把 \(i\) 换成 \(n-i\)。

\[f_{n-i}=\sum_{j=0}^{i} (-1)^{i-j}\binom{n-j}{n-i} g_{n-j}\\ = \sum_{j=0}^{i} (-1)^{i-j}\binom{n-j}{n-i} g_{n-j}\\ =\frac{1}{(n-i)!}\sum_{j=0}^{i} (-1)^{i-j}\frac{(n-j)!}{(i-j)!} g_{n-j}\\ \frac{1}{(n-i)!}\sum_{j=0}^{i} \frac{(-1)^{i-j}}{(i-j)!} (n-j)! g_{n-j} \]

后面的 \(n-j\) 部分先求出然后翻转，然后卷积，卷完之后再转回来就好了。

其实二项式反演还有其他一些式子，不过都是这个的变形而已。

---

P4491 \(\color{blue}\bigstar\)

有 \(n\) 个球，每个球可以涂成 \(m\) 种颜色之一，对于一种染色方案，记录 \(k\) 表示恰好出现 \(S\) 次的颜色数，定义染色的价值为 \(W_k\)。

求所有染色方案价值之和，答案对 \(998244353\) 取模。

\(n\le 10^7,m\le 10^5,S\le 150\)

考虑容斥，设 \(f_i\) 表示钦定 \(i\) 中颜色的方案数，\(f\) 的数组长度显然只有 \(\min(m,\frac{n}{S})\)，那么可以直接求。

\[f_i=\binom{m}{i}\binom{n}{iS}\frac{(iS)!}{(S!)^i}(m-i)^{n-iS} \]

意思就是先选出颜色，再选出位置，然后排列一下，其他位置随便选。

然后用一下二项式反演就可以计算出 \(g_i\) 表示恰好 \(i\) 个的方案了，那就可以直接算了。

code

---

多项式全家桶

除了简单的乘法，我们还需要更多的运算！

• 多项式牛顿迭代

有函数 \(G\) 与多项式 \(F(x)\)，如果 \(G\) 是较简单且已知的函数且满足 \(G(F(x))=0\)，那么久可以使用倍增求解。

设 \(f(x)\) 表示 \(F(x)\) 已经求解出的前 \(\left \lceil \frac{n}{2} \right \rceil\) 项，那么

\[F(x)=f(x)-\frac{G(f(x))}{G'(f(x))} \]

这个式子很好记，而且在下面的推导中非常方便。

证明可以先学习一下我的 微积分学习笔记 中的泰勒级数部分。

把 \(G\) 在 \(f(x)\) 处展开。

\[G(F(x))=G(f(x))+\frac{G'(f(x))(F(x)-f(x))}{1!}+\frac{G''(f(x))(F(x)-f(x))^2}{2!}... \]

此时由于 \(F(x)-f(x)\) 只有在 \(x^{\frac{n}{2}}\) 次数以上才有值，所以开平方后取模就等于 \(0\) 了。

\[G(F(x))=G(f(x))+G'(f(x))(F(x)-f(x))\\ G(f(x))+G'(f(x))F(x)-f(x)G'(f(x))=0\\ G'(f(x))F(x)=f(x)G'(f(x))-G(f(x))\\ F(x)=f(x)-\frac{G(f(x))}{G'(f(x))} \]

需要注意以下几点：

• 式子中 \(G(f(x))\) 在 \(\mod x^{\left \lceil \frac{n}{2} \right \rceil}\) 意义下显然是 \(0\)，所以 \(G'(f(x))\) 只需要保留前 \(\left \lceil \frac{n}{2} \right \rceil\) 项即可。

• \(G'(f(x))\) 是以 \(f(x)\) 为主元的求导。

• 不要随意化简，因为如果把 \(f(x)\) 项加进去，那么可能不满足第一点条件，下面的就需要保留到 \(n\) 项。

时间复杂度的话，可以发现中间的运算无论求导还是乘法都是 \(O(n\log n)\)。

\(T(n)=T(\frac{n}{2})+O(n\log n)=O(n\log n)\)。

所以多项式牛顿迭代推出的式子都是可以 \(O(n\log n)\) 做的。

---

• 多项式求逆

已知多项式 \(A(x)\)，求一个多项式 \(B(x)\) 满足 \(A(x)B(x)\equiv 1\pmod{x^n}\)。

直接套就好了设 \(G(B(x))=A(x)B(x)-1=0\)。

\[F(x)=f(x)-\frac{A(x)f(x)-1}{A(x)}=f(x)-(A(x)f(x)-1)f(x) \]

直接做就好了。

code

---

• 多项式开根

已知多项式 \(A(x)\)，求一个多项式 \(B(x)\) 满足 \(B^2(x)\equiv A(x)\pmod {x^n}\)。

也差不多。

\[G(B(x))=B^2(x)-A(x)\\ F(x)=f(x)-\frac{f^2(x)-A(x)}{2f(x)} \]

不需要化简，可以边求逆元边开方，常数比较小。

code

---

• 多项式 \(\ln\)

已知多项式 \(A(x)\)，求一个多项式 \(B(x)\) 满足 \(B(x)\equiv \ln(A(x)) \pmod {x^n}\)

不需要牛顿迭代（不会，可以直接两边同时求导。

\[\ln'(A(x))A'(x)=B'(x)\\ \frac{A'(x)}{A(x)}=B'(x) \]

先求导，求逆后再积分就好了。

code

---

• 多项式 \(\exp\)

已知多项式 \(A(x)\)，求一个多项式 \(B(x)\) 满足 \(B(x)\equiv e^{A(x)}\pmod {x^n}\)

直接牛顿迭代，\(G(B(x))=\ln(B(x))-A(x)\)

\[F(x)=f(x)-(\ln(f(x))-A(x))f(x) \]

直接做就好了。

code

代码好像有些问题，长度需要开成 \(2n\)？正确代码可以看下面的全套模板

---

多项式计数题泛做

全套模板

你已经会了多项式的基本运算了，让我们向更难的题进军！

可以先阅读 普通生成函数。

---

CF438E *3100 \(\color{green}\bigstar\)

有一个大小为 \(n\) 的集合 \(S\)，对于每个 \(1\le s\le m\)，求出有多少棵二叉树满足每个点的点权 \(x\in S\) 且 \(\sum x=s\)。

设 \(f_i\) 表示 \(s=i\) 的答案，\(g_i\) 表示 \(i\) 在 \(S\) 中的出现次数，那么：

\[f_n=\sum_{i+j+k=n} f_if_jg_k \]

显然卷积形式，但是是三个卷，写成生成函数：

\[F=1+F^2G \]

加上 \(1\) 是因为 \(f_0=1\)。

\[F=\frac{1\pm \sqrt{1-4G}}{2G}=\frac{2}{1\mp \sqrt{1-4G}} \]

显然下面是减号会寄，所以取加号，然后多项式开根+求逆就好了。

需要注意的是写开根和求逆要开大数组。

code

---

P4389 \(\color{blue}\bigstar\)

有 \(n\) 种物品，每种物品数量无限，体积为 \(v_i\)，求对于每个 \(s\in [1,m]\) 求出有多少种方案选出一些物体使得体积和为 \(s\)。
\(n,m\le 10^5\)

经 典 老 题。

直接考虑每个物体的生成函数，就是 \(\sum x^{iV}=\frac{1}{1-x^V}\)。

答案相当于求 \(\prod \frac{1}{(1-x^{v_i})}\)。

可以把下面的乘积求出来然后求个逆。

下面这个东西项数很少，指数很大，不能用分治 NTT，考虑求一个 \(\ln\) ，这样加起来再求个 \(\exp\) 就好了。

考虑求 \(\ln\) 咋做。

\[\ln(1-x^V)=F\\ \frac{-Vx^{V-1}}{1-x^V}=F'\\ =-Vx^{V-1}\sum_{i=0} x^{iV}\\ =-\sum_{i=1}Vx^{iV-1}\\ F=-\sum_{i=1} \frac{x^{iV}}{i} \]

所以开桶之后就可以 \(O(n\log n)\) 计算 \(\ln\) 之和了。

code

---

CF623E *3300 \(\color{Gold}\bigstar\)

对于一个整数序列 \(\{a_1, a_2, \ldots, a_n\}\)，我们定义它的变换为 \(\{b_1, b_2, \ldots, b_n\}\)，其中 \(b_i = a_1 | a_2 | \ldots | a_i\)，其中 \(|\) 表示二进制按位或运算。
现在求有多少个长为 \(n\) 的序列 \(a\)，满足 \(1\leq a_i \leq 2^k - 1\)，使得它的变换 \(b\) 是严格单调递增的，对 \(10^9+7\) 取模。
\(1\leq n \leq 10^{18}\)，\(1\leq k \leq 3 \times 10^4\)。

貌似是一个比套路的卷积优化 dp 题。

首先每次必然要让至少一位变成 \(1\)，所以 \(n>k\) 必然无解。

设 \(f_{i,j}\) 表示前 \(i\) 个数的或和二进制位上有 \(j\) 个 \(1\) 的方案数。

那么容易得到状态转移方程：

\[f_{i,j}=\sum_{k=1}^j f_{i-1,j-k}\binom{j}{k}2^{j-k} \]

就是枚举这次让那些位变成 \(1\)。

这个东西一眼卷积，时间复杂度 \(O(n^2\log n)\)，寄，我感觉是变成一个多项式的 \(n\) 次幂的形式，推了半天无果，看题解。

考虑上面一次转移第一维变了 \(1\) ，可以考虑变多一些。

根据组合意义，得到：

\[f_{x+y,j}=\sum_{k=1}^j f_{x,k}f_{y,j-k}\binom{j}{k}2^{ky}=j!\sum_{k=1}^j (\frac{f_{x,k}2^{ky}}{k!})\frac{f_{y,j-k}}{(j-k)!} \]

就是考虑后面 \(y\) 步选了 \(j-k\) 个。

这东西显然可以一遍卷积处理，所以就可以倍增做了，时间复杂度 \(O(n\log^2 n)\)。

没马出题人，模数 \(10^9+7\)，需要写 MTT，nmsl。

code

---

ABC260Ex *3339 \(\color{red}\bigstar\)

已知一个长度为 \(n\) 的序列 \(a\)，定义一个排列 \(p\) 的价值 \(C(p)\) 满足 \(a_{p_i}\ne a_{p_{i+1}}\) 的 \(i\) 的个数，\(S\) 表示所有排列的集合，对于每个 \(1\le k\le m\)，求

\[\sum_{p} C(p)^k \]

答案对 \(998244353\) 取模。

\(n,m\le 2.5\times 10^5\)。

牛逼题，做了很久。

这个式子直接做很困难，但是考虑到 \(0\le C(p)<n\)，所以可以先求出 \(a_i\) 表示有多少 \(C(p)=i\)，然后再求答案。

考虑 \(a\) 怎么求。

可以发现相邻位置不同这个东西很难搞，因此考虑 \(n-1\) 减去相同的即可。

那么算相同的呢，先考虑排列一下，然后选择若干个间隔变成相同的。但这样会发现分出来的每一块是等价的，因为如果改变顺序就总有另一种方案与之重复，所以可以得到单个颜色数位 \(t\) 的生成函数。

这实际上是个容斥，计算的是钦定 \(i\) 个的方案。

\[f(x)=t!\sum_{i=0}^{t-1} \frac{\binom{t-1}{i}}{(t-i)!}x^i \]

全部卷起来，然后把 \(f_i\) 乘上 \((n-i)!\) 即可。

这是钦定的，那么直接二项式反演一下变成恰好的即可，然后再翻转一下就得到了 \(a\)。

然后设 \(g_i\) 表示 \(k=i\) 时的答案。

\[g_n=\sum a_ii^n \]

这个次方斯特林数不大能搞，考虑直接生成函数。

\[G(x)=\sum_n g_n x^n=\sum_n (\sum_i a_ii^n)x^n=\sum_i a_i(\sum_n i^nx^n)\\ =\sum_i \frac{a_i}{1-ix} \]

直接分治 NTT+ 多项式求逆就可以求出这个多项式了。

这个题比较阿拉丁，而且比较卡常，如果卡不过可以减少取模，或者在这个分治 NTT 里三次卷积运算的 \(9\) 次 NTT 优化成 \(6\) 次，也可以开 Ofast

code

---

loj 6703 \(\color{Gold}\bigstar\)

定义一个序列 \(a_{1\ldots k}\) 的权值为 \(\prod_{i = 1}^k(a_i + i)\)。

现在小 Q 有一个长度为 \(n\) 的序列 \(c_{1\ldots n}\)。 他想知道他的序列的所有 \(2^n - 1\) 个非空子序列的权值和。
由于答案很大，你只需要输出答案对 \(998244353\) 取模的结果。

\(n\le 10^5\)。

这个式子和斯特林数比较像就考虑组合意义的 trick 比较牛逼。

先考虑一个 \(O(n^2)\) 的 dp，令 \(f_{i,j}\) 表示前 \(i\) 个数里选了 \(j\) 个的答案。

\[f_{i,j}=f_{i-1,j-1}\times (j+c_i)+f_{i-1,j} \]

可以发现这个式子和第二类斯特林数比较像，先把第二维换成 \(i-j\)，可以得到

\[f_{i,j}=f_{i-1,j}\times (i-j+c_i)+f_{i-1,j-1} \]

把 \(f_{i,j}\) 乘上 \(-1^{i+j}\)，可以得到

\[f_{i,j}=f_{i-1,j}\times (j-c_i-i)+f_{i-1,j-1} \]

然后来分析其组合意义，如果是加 \(j\) ，那么就相当于有 \(m\) 个盒子，然后放 \(n\) 个球，每个球还有 \(-c_i-i\) 个专属的盒子可以放的方案数，令 \(b_i=c_i-i\)。

然后直接容斥前面有多少个盒子为空，可以得到：

\[f_{n,m}=\frac{1}{m!}\sum_{i=0}^m (-1)^i \binom{m}{i} \prod_{j=1}^n (b_j+m-i) \\ \]

问题变成考虑快速求 \(g(x)=\prod_{i=1}^n (b_i+x)\) 的点值。

这个东西可以直接用分治 NTT+多项式快速求值做，但是常数大而且我不会。

但考虑我们只需要求 \([1,n]\) 范围内的点值就可以了，考虑进行分治，对于当前区间 \([l,r]\)，求出 \([0,r-l]\) 在这个区间内的点值。

然后考虑怎么把两个区间进行合并，左边的点值都已知，那么可以使用 P5667，的做法，进行一次多项式卷积就可以计算出右边的点值，那么相加就可以得到右边的在整个区间的点值，这样通过两次卷积就可以合并两个区间了，时间复杂度自然就是 \(O(n\log^2 n)\)。

最后求就很简单了。

\[f_{n,m}=\frac{1}{m!}\sum_{i=0}^m (-1)^i \binom{m}{i} g_{m-j} \\ =\sum_{i=0}^m \frac{(-1)^i}{i!}\frac{g_{m-i}}{(m-i)!} \]

直接卷积就可以求答案了。

真的好阿拉丁啊，写了一天（虽然一直在摆烂），结果最后的原因竟然是 NTT 里预处理把 \(m\) 写成了 \(n\)。

code

---

ARC134F *3530 \(\color{Gold}\bigstar\)

已知 \(n,W\)，开始时有 \(n\) 个硬币，每一个都朝上，对于一个排列 \(p\)，其价值定义为：

对于 \(1\le i\le n\)，顺次进行操作。

• 如果 \(i\) 朝上，那么把 \(i\) 和 \(p_i\) 都翻面。

• 否则什么也不做。

如果最后有 \(k\) 枚硬币朝上，那么价值就是 \(W^k\)，求所有排列价值之和。

\(n\le 2\times 10^5\)，答案对 \(998244353\) 取模。

显然先考虑置换环，先 \(i\) 与 \(p_i\) 连边，那么会形成一堆置换环，只需要对每个置换环分别做即可。

考虑对于一个置换环，先拿出一个最小的点放在开头，破环成链，然后答案就相当于是长度为奇数的极长子串个数。

既然是奇数，那么可以直接把相邻两个填上 AB，然后最后多出来的哪一个填上 C，答案就是考虑 C 的个数。

已知一个字母序列，如何确定填数的方案数呢？考虑其实只需要满足 B 大于前面 A，A 小于前面的 C 即可，其他东西都不用满足，但是这样会出现一个问题，就是填数时后面的可能会比第一个要小，不满足前面的条件，会算重。

考虑多个环放在一起，可以这样考虑，把环首从大到小排序然后顺次放，这样保证了后面的不会影响前面的了，然后就相当于考虑一个字母序列填数的方案数，并且可以发现这样排放后形成的序列与原排列一一对应。

可以发现合法的字母序列形如 CCCABCCCABCCCAB...ABCCC 的形式，两个 AB 中间可能也没有 C。

可以直接把若干个 C 和 AB 捆在一起，这样两组之间就没有约束条件，最后的 C 最后考虑，然后相当于每次放一个组进去。

那么形如 CCCCCAB 这样的填数方案有多少种呢，可以发现满足 \(C>A<B\) 即可，那么只需要拿出一个数当 B ，最小的数当 A 即可，因此一个长度为 \(n\) 一组字母的方案数是 \((n-1)\)，然后序列方案数就可以直接 dp 求了，设 \(f_i\) 表示前 \(i\) 个的填数方案数，可以得到：

\[f_i=\sum_{j=2}^i \binom{i}{j}W^{j-2}(j-1)f_{i-j}\\ \frac{f_i}{i!}=\sum_{j=2}^i W^{j-2}(j-1)j!\frac{f_{i-j}}{(i-j)!} \]

这里可以直接 \(O(n\log^2n)\) 的分治 FFT 求解了，下面考虑用生成函数优化，假设 \(f\) 的 EGF 是 \(\hat F\)，然后设 \(W^{j-2}(j-1)\) 的 EGF 是 \(\hat G\)，那么列方程，注意加上初值。

\[\hat F=1+\hat G\times \hat F\\ \hat F=\frac{1}{1-\hat G} \]

直接多项式求逆即可。

code

---

ABC213Ex *2806 \(\color{blue}\bigstar\)

有 \(n\) 个点，一个人从 \(1\) 出发，每次走一条边，现在有 \(M\) 条边，第 \(i\) 种边连接 \((a_i,b_i)\)，有 \(p_{i,j}\) 种方式走过这条边且长度为 \(j\)，求有多少种方式使得走长度恰好 \(T\) 的距离并且回到 \(1\) 的方案数，答案对 \(998244353\) 取模。

\(n\le 10,M\le 10,T\le 4\times 10^4\)。

先考虑一个 naive 的 dp，设 \(f_{i,j}\) 表示走到 \(i\)，距离为 \(j\) 的方案数，那么可以发现转移就是直接按 \(j\) 进行一层一层的转移。

那么一个简单的想法就是类似分治 FFT，考虑前面的给后面的贡献可以直接用卷积计算即可，这样复杂度就是 \(O(MT\log^2T)\)，可过。

code

还有另一个做法。

考虑用邻接矩阵存图，那么走两步就是矩阵乘法，这样就相当于等比数列求和，可以直接即可，暴力做复杂度 \(O(n^3T\log^2 T)\)，寄。

考虑矩阵乘法中乘法是多项式卷积，上面的做法是暴力 \(O(T\log T)\)，但是可以发现可以直接先全部 DFT，然后矩阵乘法是直接点乘，然后再 IDFT 回来即可。

然后复杂度就是 \(O(n^2T\log^2 T+n^3T\log T)\)。

---

ABC267Ex *2422 \(\color{green}\bigstar\)

有 \(n\) 个数，需要在其中选奇数个使得和为 \(M\)，求方案数。

\(n\le 10^5,M\le 10^6,a_i\le 10\)。

一眼就会了，求组合数没有取模调半天。

直接设 \(f_i,g_i\) 分别表示和为 \(i\)，选了奇数、偶数个数的方案数，那么开桶统计每个数出现的次数，那么一个数选若干个的方案数可以直接算，然后卷积加起来即可。

暴力做是每次四个卷积，会 T，可以先 DFT，加完再 IDFT 回来。

code

---

ABC269Ex *3178 \(\color{Gold}\bigstar\)

有一棵 \(n\) 个点的树，对于 \(1\le x\le n\) 中的每一个 \(x\)，求出有多少种方案选出一个大小为 \(x\) 的反链（也就是选出一个集合，满足其中任意 \(x,y\) 都满足没有祖先关系）。

\(n\le 2\times 10^5\)。

好题，先设 \(f_{x,y}\) 表示 \(x\) 子树中选 \(y\) 个的方案数，那么设 \(F_x\) 是其生成函数，容易得到：

\[F_{x}=1+x+\sum_{y\in son} F_y \]

然后一直想着怎么维护 dft 后的结果，发现加上 \(1+x\) 不会搞，寄。

正解还是比较高妙的，考虑先树剖一下，然后对于每条链的顶端计算答案。

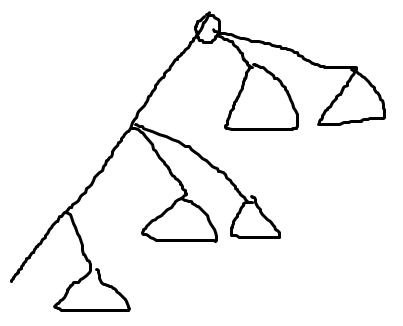
就长这样。

然后可以发现，对于链上每个点，先把不在链上的儿子卷起来，然后考虑怎么合并。

考虑链上最多选一个，考虑选哪一个，那么接下来选的只能是它上面的链上的点对应的子树，因此就是一个后缀和，直接分治即可，注意有一个都不选的情况。

code

---

ANTUTREE *3300 \(\color{Gold}\bigstar\)

牛逼题。

加入一条边的连通块大小比较难算，直接考虑每个点对答案的贡献，如果把这条边对应的两个点合并成一个点然后把这个点作为根建树，容易发现相当于要先加入这个点到根路径上所有的边，然后再加入根的边。

问题变成要求 \(x\) 个东西要比一个指定的东西先选的概率，一开始以为是 \(\frac{1}{2^x}\)，sb 了，事实上应该是 \(\frac{1}{x+1}\)，这个可以简单证明。

然后问题变成对于每条边，求

\[\sum \frac{1}{d+1} \]

想了半天换根，不会。

看了一眼题解，发现是“点分治+FFT”，然后会了。

考虑计算所有经过分治中心的路径，以分治中心为根求出所有点的距离，一个是 \(a\)，另一个是 \(b\)，那么求可以产生 \(\frac{1}{a+b}\) 的贡献，然后一个点分治经典做法就是先做全部再减去子树内的，那么一个深度为 \(a\) 的答案可以表示成。

\[f(a)=\sum_{b=0}^L c(b)\frac{1}{a+b} \]

\(c(b)\) 表示深度为 \(b\) 的个数，直接把 \(c\) 翻转一下就变成卷积形式，直接卷积即可，复杂度 \(O(n\log^2n)\)。

P4500 \(\color{red}\bigstar\)

这是真的，屁也不会，群论推半天感觉没啥用。

参考link，做了一定的补充（？

注意题目同构的定义是有根的。

首先注意到本质是要求

\[\text{Ans}=\sum_{x\in X/G} (\frac{|x|}{|X|})^k \]

然后注意到每个轨道可以表示为一棵无标号有根树，用 \(T\) 来代替轨道 \(x\)，然后令 \(f(T)\) 表示与 \(T\) 同构的方案数，也就是 \(|x|\)。

直接瞎数一下，可以得到：

\[f(T)=|T|!\prod_{u\in T} \frac{1}{siz_u}\prod_{u\in T}w_u \]

后面的 \(w\) 是因为 \(u\) 的两个儿子的子树可能同构，需要去掉。

这样有一个好处是式子是乘法而不是加法，取 \(k\) 次方非常方便。

\[\text{Ans}=\frac{1}{((n-1)!)^k}\sum_{|T|=n} f^{k}(T) \]

反手设一个 \(dp_{n,m}=\sum_{|T|=n}f^m(T)\)，然后去求。

换用一个求无标号树的套路，把根拿出，然后它的子树相当于一个背包。

\[dp_{n,m}=\frac{(n!)^m}{n^m}[x^n]x\prod_{i=1} \prod_{|T|=i}\sum_{j=0} \frac{x^{ij}f^{jm}(T)}{(j!)^m(|T|!)^m} \]

注意到这个式子有点引荐了，不妨换一下 \(f\) 的定义，修改为：

\[f(T)=\prod_{u\in T} \frac{1}{siz_u}\prod_{u\in T}w_u \]

\(dp,\text{Ans}\) 也同理修改。

\[dp_{n,m}=\frac{1}{n^m}[x^{n-1}]\prod_{i=1} \prod_{|T|=i}\sum_{j=0} \frac{f^{jm}(T)}{(j!)^m}x^{ij}\\ \text{Ans}=n^k dp_{n,k} \]

把后面东西拉出来：

\[A_n=\prod_{i=1} \prod_{|T|=i}\sum_{j=0} \frac{f^{jm}(T)}{(j!)^m}x^{ij}\\ =\exp(\sum_{|T|\le n} \ln(\sum_{j=0}\frac{f^{jm}(T)}{(j!)^m}x^{|T|j})) \]

\(\ln\) 里面东西无法做，但是我们可以去把 \((f^m(T)x^{|T|})\) 换元一下，然后求出这个 \(\ln\) 会在前面乘上的系数，本质上就是多项式复合的定义，但是需要满足 \(\ln\) 有常数项。

可以这么做的本质是，多项式 \(\ln\) 是泰勒展开，因此相当于每一项去卷上 \(\ln x\) 的展开式。

设：

\[B=\ln(\sum_{j=0}\frac{x^j}{(j!)^m}) \]

好处是这个东西只和 \(m\) 有关，可以暴力预处理。

\[A_n=\exp(\sum_{|T|\le n} \sum_{j=0} ([x^j]B)f^{jm}(T)x^{|T|j} )\\ =\exp(\sum_{j=0}([x^j]B) (\sum_{|T|\le n} f^{m}(T)x^{|T|})^j ) \]

现在回想一下我们咋能求出答案，显然是要对 \(dp\) 进行递推，也就是我们需要知道 \(dp\) 的递推式即可。

\[dp_{n,m}=\sum_{|T|=n}f^m(T)\\ =\frac{1}{n^m}[x^{n-1}]\exp(\sum_{j=0}([x^j]B) \sum_{|T|\le n} f^{mj}(T)x^{|T|j}) \]

注意到上下两个东西在后面那个地方是很像的，但是下面是 \(f^{mj}(T)\)，考虑修改 \(dp\) 的定义使得可以适应这个东西。

令

\[dp_{n,m}=\sum_{|T|=n}f^{mk}(T) \]

\(k\) 是题意中选 \(k\) 棵树。

由于只是把 \(m\) 换成了 \(mk\)，因此直接可以得到对于新的 \(dp\)：

\[B_m=\ln(\sum_{j=0} \frac{x^j}{(j!)^{mk}})\\ dp_{n,m}=\frac{1}{n^{mk}}[x^{n-1}]\exp(\sum_{j=0}([x^j]B_m) \sum_{|T|\le n} f^{mkj}(T)x^{|T|j})\\ =\frac{1}{n^{mk}}[x^{n-1}]\prod_{i} \exp(\sum_{j=0}([x^j]B_m) \sum_{|T|=i} f^{mkj}(T)x^{ij})\\ =\frac{1}{n^{mk}}[x^{n-1}]\prod_{i} \exp(\sum_{j=0}([x^j]B_m) dp_{i,mj}x^{ij}) \]

最后要求的就是 \(dp_{n,1}\)。

注意到后面有一个 \(x^{ij}\)，也就是 \(ij<n\)（此处是 \(dp\) 下标里的 \(n\)），那么 \(j<n/i\)，容易证明对于可能对答案有贡献的 \(dp_{i,j}\) 满足 \(ij\le n\)。

终于有做法了，就是考虑记录对于每个 \(m\) 的前缀卷积，然后正常做就行。

最后的问题是 \(O(n^2)\) 的多项式 \(\exp,\ln\)。

\[A=e^{B}\\ B=\ln A \]

下面式子两边求导：

\[B'=\frac{A'}{A}\\ xAB'=xA'\\ na_n=\sum_{i=1}^n ia_ib_{n-i} \]

然后就可以做了。

像这种数数题，lg 题解中很多直接给出修改定义后的 \(dp\) 有点离谱了，感觉就是为了讲做法而讲做法，导致像我这样不会做的人完全无法理解思考过程啊。

事实上关键性的步骤是：拆成子树的背包，用 \(B\) 代换掉 \(\ln\)，以及重新设计 \(dp\) 意义。