4月杂题选做
上回说到:2022.3(part2)
关于难度
\(\color{gray}\bigstar\) 可以秒杀的题。
\(\color{green}\bigstar\) 思考一会儿后可以秒的题。
\(\color{blue}\bigstar\) 需要较长时间思考的题。
\(\color{Gold}\bigstar\) 看题解、稍加指点就会做的题。
\(\color{red}\bigstar\) 看题解后需要较长时间消化,甚至现在都没有完全理解的题。
开始刷(贺) *2600~*2700。
CF1295F *2700 \(\color{Gold}\bigstar\)
\(a_i\) 在 \([l_i, r_i]\) 等概率随机,求 \(a_{1 \dots n}\) 不增的概率(\(a_i\) 为整数),答案对 \(998244353\) 取模。
\(n\le 50,l_i,r_i\le 998244353\)。
标签:dp,组合。
考虑一个暴力 dp,设 \(f_{i,j}\) 表示到了第 \(i\) 个,选了 \(j\) 的合法方案数。
时间复杂度 \(O(n^2\max(r_i))\),爆炸。
一个显然的思路是可以考虑离散化。
离散化后相当于变成了一堆左闭右开的区间,然后此时可以设 \(f_{i,j}\) 表示 \(i\) 在第 \(j\) 个区间的方案数。
咋转移?考虑枚举一下第一个不在第 \(j\) 个区间的第一个 \(k\),然后直接计算组合数转移即可。
注意要后缀和,然后做完了,时间复杂度 \(O(n^3)\)。
ABC246Ex *2677 \(\color{Gold}\bigstar\)
已知一个长度为 \(n\) 的字符串 \(S\),含有
0,1和?,其中?是通配符(可以任意选择变成0或者 ```)。
有 \(Q\) 次操作,每次操作修改一个位置,然后询问该串有多少个不同的非空子序列。
\(n,Q\le 10^5\)。
标签:动态dp,矩阵,线段树。
ddp 不会,赛时没想出来,其实还是比较板子的。
考虑如果一次询问咋做,考虑 dp。
设 \(f_{i,0/1}\) 表示前 \(i\) 个字符,结尾为 0/1 的子序列有多少个。
考虑 \(s_i=0\) 咋转移。
显然 \(f_{i,1}=f_{i-1,1}\)。
考虑 \(f_{i,0}\),如果是 \(1...i-1\) 中出现的,那么就是 \(f_{i-1,0}\),否则必须选择 \(s_i\)。
多了一个 0,本质上增加的就是在前面每一个 1 后面放尽量多的 \(0\) 后面再放一个 \(0\),注意可以全部都放 \(0\),这部分贡献为 \(f_{i-1,1}+1\)。
所以 \(f_{i,0}=f_{i-1,0}+f_{i-1,1}+1\)。
然后咋维护修改呢?
发现这个东西可以写成矩阵形式,相当于一堆矩阵乘起来,由于矩阵乘法满足结合律,所以用线段树随便维护就好了。
ABC246G *2313 \(\color{blue}\bigstar\)
已知一棵树,\(1\) 为根,有点权,开始有一个石头在 \(1\) 号节点,小 A 小 B 轮流操作。
小 A 每次把一个没有石头的点点权变成 \(0\),小 B 每次可以选择结束游戏或者把石头移动到它的任意一个子节点。
最后得分是结束时石头所在位置的点权。
小 A 想让这个值最小,小 B 想让这个值最大,求最后的得分是多少。
\(n\le 10^5,a_i\le 10^9\)。
标签:二分,dp。
考虑先用二分答案,把点权分成 \(>mid\) 和 \(<mid\) 两部分,然后变成判定性问题。
使用 dp,设 \(f_i\) 表示把石头移到 \(i\) 之前,该子树至少进行多少次操作。
容易得到式子:
其中 \(p_{son}\) 表示是否大于 \(mid\)。
直接做,判断 \(f_1\) 是否是 \(0\) 即可。
CF840C *2500 \(\color{green}\bigstar\)
给定一个长度为 \(n\) 的序列 \(a\),求有多少 \(1\) 到 \(n\) 的排列 \(p_i\) 满足对于任意的 \(2\le i\le n\) 有 \(a_{p_{i-1}}\times a_{p_i}\) 不为完全平方数,答案对 \(10^9+7\) 取模。
\(n\le 300,a_i\le 10^9\)。
有 \(O(n^3)\) 的 dp 做法,但是好像很困难,来个容易想到的 \(O(n^2)\) 容斥做法。
首先把每个 \(a_i\) 含有的完全平方数除掉,这样的话相当于不能让两个相同的数相邻。
容斥一下,钦定 \(i\) 对相邻的数相同,把这些相同的合并一下,那么排列的方案数就是 \((n-i)!\),然后计算一下选出这 \(i\) 对的贡献。
分别考虑每一种数,然后合并相当于是一个卷积,可以暴力卷积。
每一种数的方案相当于是一个完全图,从中随便选一条边,然后把两个点合并,注意是有向边,而且选边的顺序无关。
时间复杂度 \(O(n^2)\)。
CF1473F *2700 \(\color{blue}\bigstar\)
你有两个长度均为 \(n\) 的序列 \(a_1,a_2,\dots,a_n\)。
我们定义一个集合 \(S\subseteq \{1,2,\dots,n\}\) 是奇怪的,当且仅当:对于任意 \(i\in S\),如果有 \(j\in [1,i-1]\),满足 \(a_j|a_i\),则也有 \(j\in S\)。特别地,空集总是一个奇怪的集合。
定义一个集合 \(S\) 的权为 \(\sum_{i\in S} b_i\) 。请求出所有奇怪集合的最大权。
\(n\le 3000,a_i\le 100\),空间限制 \(32MB\)。
标签:网络流。
不难的题,但我想了好久。
考虑网络流,选择一个点的前提是选择它因数的所有点,经典网络流,与 CF1082G 差不多,考虑先把所有 \(b_i>0\) 的点加上,然后减去不合法的,进行最小割。
不合法的就是选择了一个点,但是没有选择前面的是它因数的点,一个简单的想法是原点向所有 \(b_i\) 为正的点连边权为 \(b_i\) 的边,每个点向自己因数的点连 Inf,\(b_i\) 为负的点向汇点连 \(-b_i\) 的边,然后跑最小割。
会有个问题,就是一个 \(b_i\) 为正的点可能依赖另一个 \(b_j\) 为正的点。
然后发现其实没有影响,因为如果 \(j\) 依赖 \(k\),那么 \(i\) 也一定依赖于 \(k\),所以是对的。
然后建图边数 \(n^2\) 的,寄,然后可以发现因为上面那个性质,而且 \(a_i\) 比较小,所以对于相同的 \(a_j\) ,只需要连最后一个就好了,这样边数就可以通过了。
CF1220F *2700 \(\color{green}\bigstar\)
有一个 \(1...n\) 的排列,按照这个序列建二叉树:
找最小的元素作为根。
排列被分为:这个元素的左边和右边两个部分。
左边最小元素成为左子节点,右边最小元素成为右子节点。
输出树的最小深度,及需要向左移动多少的元素才能到达这个深度。
\(n\le 2\times 10^5\)。
标签:线段树。
简单题,考虑枚举一下移动次数,把一个数移动到后面去本质上修改了一些点的深度,先求这个点自己的深度,找到前面的第一个比自己小的数,深度就是它加一,然后把它到自己这段区间中的数全部加一。
每次查询全局最大深度就做完了。
CF995F *2700 \(\color{Gold}\bigstar\)
已知一棵 \(n\) 个点,根为 \(1\) 的树,可以给树上每个节点分配一个 \([1,D]\) 的权值,要求每个节点的权值不大于其父亲节点的权值,求方案数,对 \(10^9+7\) 取模。
\(n\le 3000,D\le 10^9\)。
标签:树形 dp,容斥。
洛谷题解一车拉格朗日插值,我太菜了,根本不会。
考虑如果 \(D\le n\) 怎么做,发现这个东西很简单,直接树形 dp,考虑设 \(f_{i,j}\) 表示以 \(i\) 为根的子树中,\(a_i\le j\) 的方案数,容易得到状态转移方程:
时间复杂度 \(O(nD)\),考虑优化。
可以发现我们实际上最多用了 \(n\) 个 \([1,D]\) 的数来作为节点的权值,所以可以考虑先在 \([1,D]\) 中拿出 \(n\) 个数,然后进行一波容斥,因为权值可能相同,也就是说没有用到所有的数。
我们设 \(g_i\) 表示去重后恰好使用 \(i\) 个数的方案数。
那么相当于总数减去没有用到 \(i\) 个数的。
时间复杂度 \(O(n^2)\),个人觉得比洛谷题解中的容斥更优美一些。
CF464D *2700 \(\color{blue}\bigstar\)
题比较长,自己看吧。
标签:期望,dp。
其实不是很难的题。
会发现每个装备本质一样,可以算出一个后乘上 \(k\) 得到总答案。
考虑设 \(f_{i,j}\) 表示还剩下 \(i\) 次操作,现在装备等级为 \(j\),该武器获得的期望钱数。
分三种情况讨论,升一级,不升级直接卖,不选该装备。
然后得到一个时间复杂度 \(O(n^2)\) 的 dp。
可以发现本题没有模数,输出浮点数,有一个知名技巧是把贡献小于浮点精度的直接忽略。
可以发现如果等级很高,达到了 \(j\),那么它的期望步数是 \(\frac{1}{k(j+1)}\),当 \(j=1000\) 时,可以忽略。
所以就可以直接 dp 了。
CF241B *2700 \(\color{gray}\bigstar\)
给定 \(n\) 个整数 \(a_1,a_2...a_n\),求两两异或值前 \(k\) 大的和,答案对 \(10^9+7\) 取模。
\(n\le 50000,a_i\le 10^9\)。
标签:二分,字典树。
显然一眼可以二分答案一下,对于每个点看看异或值 \(\ge mid\) 有多少种方案,然后得到第 \(k\) 大的异或值,接下来统计答案也类似,在字典树的节点上统计其子树每一位出现次数,然后最后把每一位的答案加起来就好了。
ARC137D *2191 \(\color{green}\bigstar\)
已知一个长度为 \(n\) 的序列 \(A\),每次操作会使每个 \(A_i\) 变成 \(A_1 \bigoplus A_2 ... \bigoplus A_i\),求对于每个 \(1\le j\le m\) 求,操作 \(j\) 次后 \(A_n\) 的值。
其中 \(\bigoplus\) 表示按位异或。
\(n,m\le 10^6,A_i\le 2^30\)。
标签:卢卡斯定理,高维前缀和。
考虑每个数对答案的贡献,由于是异或。所以要么是 \(0\) 要么是 \(1\),对于一个数的贡献,可以发现每次是做一个前缀和,然后对 \(2\) 取模。
做 \(T\) 次前缀和,当前数对一个自己右边第 \(j\) 个数的贡献是 \(\binom{j+T-1}{j}\mod 2\) ,容易想到使用卢卡斯定理,这样相当于是 \(j+T-1,j\) 两个数每个二进制位的组合数之和。
想要让这个是 \(1\),就需要满足上下与起来是下面的,然后上面减去 \(j\) ,本质上就是 \((T-1)\& j=0\)。
这个直接高维前缀和一下统计一个异或和就好了。
ARC138C *1728 \(\color{green}\bigstar\)
有一个长度为 \(n\) 的序列,先手每次任意取没取过的一个数,后手每次取没取过的最前面的一个数,先手得分为选的数字之和,开始前可以把序列循环移动 \(1..n-1\) 次,找到一个 \(k\) 使得最优情况下得分最大。
\(2\le n\le 2\times 10^5\),\(n\) 是偶数。
标签:贪心。
简单题,考虑先手选的数字标记为 \(-1\),其余数字标记为 \(1\),一种合法方案就是前缀最小值 \(\ge -1\),可以发现任意一种方案都可以通过循环移位使得合法,只需要移位到出发点是最低点即可。
因此答案就是最大的 \(\frac{n}{2}\) 个数之和。
CF1601D *2700 \(\color{blue}\bigstar\)
有一座初始高度为 \(d\) 的山,有 \(n\) 个人去爬,每个人有两个属性 \(s_i,a_i\),如果 \(d\le s_i\),那么第 \(i\) 个人可以爬上这座山,然后 \(d\) 变成 \(\max(d,a_i)\),可以改变登山人的顺序,求最大登上山的人数。
\(n\le 5\times 10^5\)。
标签:贪心。
来个不需要分讨的做法。
考虑把人分成两类:\(s_i\ge a_i\) 的称为 A 类,\(s_i<a_i\) 的称为 B 类。
可以发现 A 类更为优秀,因为如果只有 A 类,只需要按 \(s_i\) 排序就可以使所有人上山,并且可以发现,最优方案中 A 类的人一定都上了山,不然一定可以在某个位置插入。
可以发现 A 类的人对 B 类没啥影响,除非 \(a_j>s_i\) 且 \(s_j<a_i\) 这样显然取 \(i\) 更优。
考虑只放 B,相当于一堆区间不能相交,求最多放几个。
一个简单做法是按右端点排序,然后贪心取。
把 A 类加入进来,发现也是按右端点排序就可以解决上面 A 对 B 的问题。
然后得到正确的贪心做法:按 \(\max(a_i,s_i)\) 排序,然后暴力取就好了。
注意一下 \(\max(a_i,s_i)\) 相等的情况,可以发现显然是先尽量取一个 B,然后全部取 A,相当于按 \(s_i\) 排序。
CF1539E *2500 \(\color{green}\bigstar\)
开始有两个数 \(a_0,a_1\),都为 \(0\),有 \(n\) 次操作,每次给一个值 \(k_i\),你需要选择两个数中的一个,把值赋成 \(k_i\),然后需要满足第 \(i\) 次操作后,\(a_0\in [l_{0,i},r_{0,i}],a_1\in [l_{1,i},r_{1,i}]\),问是否可行并构造方案。
标签:dp,st 表。
不是很难的题,可以发现每次操作后总有一个值等于 \(k_i\),考虑另一个值取什么最优,显然是可以满足向后面最多个限制条件的 \(k_j\),即使得 \(i\le t\le R, l_t\le k_j\le r_t\) 中 \(R\) 的值最大。
所以考虑设 \(f_{i,0/1}\) 表示第 \(i\) 次选 \(a_0,a_1\) ,另一个的 \(R\) 最大是多少。
找 \(R\) 可以直接倍增 st 表维护,然后转移分两种情况讨论,输出方案直接记录一下从哪个转移过来就好了。
时间复杂度 \(O(n\log n)\)。
CF474F *2100 \(\color{gray}\bigstar\)
给出一个数组\(s_i\),有 \(q\) 个询问,每个询问给出一个区间 \([l,r]\),问 \([l,r]\) 里有多少个数能整除其他数。
\(n,q\le 10^5\)。
傻*题,显然满足条件的是所有数的 \(\gcd\),线段树维护 \(\gcd\) 以及有多少个数是 \(\gcd\),乱合并就好了。
CF1367F2 *2400 \(\color{green}\bigstar\)
给定一个由 \(n\) 个正整数构成的序列(序列中可能有相同元素),每次操作可以把一个数放到开头或者结尾,现需要将该序列变成不下降序列,请问至少需要操作几次。
\(n\le 2\times 10^5\)。
加设放在前面的是 \(a\),不变的是 \(b\),扔到后面的是 \(c\),显然需要使 \(b\) 最长,并且 \(a\) 中的数都不能超过 \(b\) 中,\(c\) 中不小于 \(b\) 中,且 \(b\) 单调不增。
说明必然是 \(b\) 中含有数值在 \([l,r]\) 中的所有数字全选,然后 \(l-1\) 和 \(r+1\) 里的贪心去选。
一个简单的做法就是双指针扫 \(l,r\),然后暴力找 \(l-1\) 和 \(r+1\) 中能选多少个数,时间复杂度 \(O(n)\)。
注意可能会出现不选整段的做法,即在 \(i,i+1\) 中各选一部分,所以需要额外扫一遍。
可惜需要离散化,时间复杂度 \(O(n\log n)\)。
APC001F *2865 \(\color{red}\bigstar\)
已知一棵 \(n\) 个点的数,有边权,每次操作可以选择一条链,把链上所有边权异或上一个任意的值 \(x\),求使得所有边权都变成 \(0\) 的最小操作次数。
标签:贪心,dp。
神仙题,优秀的 trick。
一开始一直在想链修改变成两个点到根路径上的修改,然后寄了。
很妙的一个想法是考虑链上修改时,除了左右端点之外的所有在链上的点,都有两条与它相连的点被异或。
所以设 \(a_i\) 表示与 \(i\) 相连的边的异或和,然后每次操作相当于只修改了两个点的点权,并且可以发现,边权为零的话点权也为零,目标变成点权变成零。
如果两个 \(a_i\) 相同,最优操作显然一次操作把这两个点都变成零,所以接下来每个权值最多出现一次。
考虑 \(a_i\) 很小,直接状压。
设 \(f_i\) 表示权值集合为 \(i\) 的最小操作次数,可以发现必须满足集合中的数异或和为 \(0\) 才有解。
然后可以发现异或和为零的集合至多 \(|S|-1\) 次就可以全消完,原因显然。
所以可以考虑枚举当前集合的一个子集,算一下和,然后得到最小操作数即可。
CF1656F *2600 \(\color{Gold}\bigstar\)
已知一张 \(n\) 个点的完全图,\((i,j)\) 边权为 \(a_i\times a_j+t(a_i+a_j)\),其中 \(t\) 为常数,定义 \(f(t)\) 表示这个图的最小生成树,求 \(\max f(t)\),如果没有最大值,输出
INF。
\(n\le 2\times 10^5\)。
标签:贪心。
考虑如果已知一个 \(t\) 咋做,先把 \(a\) 从小到大排序。
先把式子化简一下。
\(t^2\) 为常数,不管。
由于是最小生成树,所以尽量连最小的,所以如果 \(a_i+t\) 是正数,那么尽量去连最小的最小的 \(a_1\),如果是负数,尽量连最大的 \(a_n\)。
所以相当于一个前缀连 \(a_n\),一个后缀连 \(a_1\)。
可以考虑这个前后缀分界点在哪里,然后可以分别得到一条关于 \(t\) 的函数图像,最小生成树就是一个凸壳。
本来以为要维护,很阿拉丁,但其实不用,因为最大值一定出现在两条函数的交接点,交接点出如果分界点是 \(i\),\(t=-a_i\) 是就是分界点,直接找最大值即可。
判断无解直接找两个极限的 \(t\),判断一下是否收敛即可。
开始板刷 ARC ,*2000 以下的就跳了,先从远古场做起。
ARC059E *2189 \(\color{green}\bigstar\)
题目比较长,自己看吧。
标签:dp。
简单题,显然考虑 dp,设 \(f_{i,j}\) 表示前 \(i\) 个人分 \(j\) 个糖最后式子中的和,然后相当于枚举一下 \(i\) 选几颗糖。
状态转移方程:
显然后面 \(\sum_{p=a_i}^{b_i}p^k\) 可以直接预处理用前缀和做,然后直接 dp 即可,时间复杂度 \(O(n^3)\)。
ARC059F *2427 \(\color{green}\bigstar\)
有一个字符串,开始为空,每次可以在后面添加一个 \(0\) 或者 \(1\),也可以选择删去最后一个字符,求 \(n\) 次操作后等于目标串 \(S\) 的方案数。
如果串为空,则使用删除操作不会对串产生影响。
\(n\le 5000\)。
标签:dp。
见过的最简单的 ARC F 题。
考虑由于最后需要变成目标串,相当于最后操作剩下的 \(|S|\) 个字符全部赋值为 \(S\) 即可。
可以发现只有删去的数可以在 \(01\) 之中任意选择。
如果串为空不能使用删除,那显然是一个卡特兰数。
考虑 dp,设 \(f_{i,j}\) 表示操作 \(i\) 次,得到的串长度为 \(j\) 的方案数。
如果使用删除,方案数乘 \(2\),因为被删去的那个操作可以 \(01\) 任意选,如果添加,则只能添加与 \(S\) 一样的。
所以得到状态转移方程:
取 \(\max\) 是因为如果串长度为 \(0\) 可以继续使用删除,但没有与之对应的添加操作。
ARC060D *2261 \(\color{blue}\bigstar\)
定义 \(f(n,b)\) 表示把 \(n\) 转成 \(b\) 进制数后各位数之和,已知 \(n,f(n,b)\),求最小的 \(b\)。
\(n,f(n,b)\le 10^{11}\)。
标签:根号分治。
不难的题,但我想了好久。
考虑 \(f(n,b)=f(\frac{n}{b},b)+n \mod b\)。
看到关于整除的式子考虑根号分治一下,
如果 \(b\le \sqrt{n}\),可以直接暴力做,时间复杂度 \(O(\sqrt{n}\log n)\)。
如果 \(n=b>\sqrt{n}\),可以发现 \(f(n,b)=\frac{n}{b}+n\mod b\),那么直接枚举 \(\frac{n}{b}\),然后算出 \(n\mod b\),直接减去余数除以商就是除数了,时间复杂度 \(O(\sqrt{n})\)。
可以平衡复杂度到 \(O(\sqrt{n\log n})\),不过没什么意义。
几个坑点是:可能 \(s=n\),此时 \(b=n+1\),如果 \(b=\sqrt{n}\),可能会出现 \(b\) 进制下是 \(100\) 的情况,需要在第一类中算。
ARC060E *2154 \(\color{gray}\bigstar\)
有 \(n\) 个点,第 \(i\) 个点坐标为 \(x_i\),每次可以走到一个与当前点距离不超过 \(L\),的点,\(Q\) 次询问,每次询问从 \(a\) 走到 \(b\) 最少需要几次行走。
\(n\le 10^5\)。
标签:倍增。
一眼倍增,设 \(f_{x,k}\) 表示从 \(x\) 出发走 \(2^k\) 次后到达那个店,直接跳就好了。
时间复杂度 \(O((n+Q)\log n)\)。
ARC060F *2804 \(\color{blue}\bigstar\)
定义一个串 \(S\) 是好的,当前仅当不存在一个串 \(T\) 和一个数 \(x\),满足 \(x\ge 2\),且把 \(T\) 重复 \(x\) 次后等于 \(S\)。
现在已知一个串 \(A\),需要把它分成若干个子串,使得每个子串都是好的,且子串数最少,求最少子串数以及方案数。
\(n\le 5\times 10^5\)。
标签:字符串。
首次自己做出 *2800+。
先考虑判断一个串是否是好的。
可以用字符串相关知识得到先跑一遍 KMP 之后判断 \(n\mod (n-nex_n)\) 即可,特判一下 \(nex_n=0\) 的情况。
考虑 \(O(n^2)\) 咋做,考虑 dp,设 \(f_i\) 表示前 \(i\) 个字符的答案,直接做就好了。
可以发现答案段数要么是全部相等,答案为 \(n\),要么整段是个好的,答案是 \(1\),要么就把最后一个字符扔掉,变成两个好串,方案数可以枚举分割点,然后前后各判断,后面判断可以直接倒着做一遍 KMP。
时间复杂度 \(O(n)\)。
来具体证明一下上面可以分成两段的结论。
反证法,假设存在一个长为 \(x\) 的串是 \(S_{1..n-1}\) 的整周期,长为 \(y\) 的串是 \(S_{1,n}\) 的整周期。
显然 \(\gcd(x,y)=1\),\(\gcd(x,y)|\gcd(n,n-1)=1\)。
然后可以发现 \(S_{1}=S_{1+x}=S_{1+y}=S_{1+ax+by}\)
根据某知名定理可以发现 \(S\) 中每个字符都相等,矛盾。
可以总结为引理:
如果一个长度为 \(n\) 的字符串有最长整周期为 \(x\),那么一个长度为 \(m\) 的前缀的最长整周期长度最大为 \(\gcd(x,m)\)。
ARC061E *2502 \(\color{gray}\bigstar\)
已知 \(n\) 个点 \(m\) 条边,边有边权,一条路径如果两条相邻的边边权不相同代价加一,求 \(1\) 走到 \(n\) 最小代价。
\(n,m\le 2\times 10^5\)。
标签:图论,BFS。
显然建虚点,对于相同边权的边连的点建联通块,然后虚点取连联通块中每一个元素,直接跑 bfs 即可。
P6628 \(\color{purple}{省选/NOI-}\) \(\color{blue}\bigstar\)
有一张完全图,第 \(i\) 个点到第 \(j\) 个点的边权为 \(|i-j|\),有 \(m\) 条重要边,询问对于每个 \(1\le i\le n\),从 \(s\) 出发,到 \(i\) 结束,经过每条重要边至少一次的最小边权和。
标签:欧拉回路,最小生成树。
贪心思路就是每条边经过一次,可以发现这个东西是一个欧拉路,可以考虑 \((s,i)\) 连一条边,这样相当于一个欧拉回路。
会有问题就是可能有奇点,奇点处理比较简单,相邻的连边即可,并且为了尽量联通,所以把这段区间中所有的数都连成一条链。
联通块可以用并查集动态维护。
然后是联通的问题,无脑最小生成树后边权乘 \(2\) 即可。
P7516 \(\color{purple}{省选/NOI-}\) \(\color{green}\bigstar\)
题比较长,自己看吧。
标签:最短路。
这题 \(O(n^3)\) 可过真是离大谱。
考虑两个点对答案的贡献。
如果 \(u>v\) ,那么 \((u,v)\) 对答案有贡献需要满足 \(u\) 到 \(v\) 路径上的点都大于 \(u\),并且 \(v\) 到 \(u\) 路径上的点都大于 \(u\),在此基础上边出现时间最大。
反证一下,如果存在一个点 \(x\) 在 \(u\) 到 \(v\) 路径上满足 \(x<u\),那么 \(x\) 必然可以在前面就被删除,反过来也同理。
因此相当于从大到小加边,跑 \(O(n^3)\) 最短路即可,然后做一个后缀和就好了,注意卡常。
CF1592F1 *2600 \(\color{Gold}\bigstar\)
有一个 \(n\times m\) 的 \(01\) 目标矩阵,你可以进行四种操作:
- 选择一个包含 \((1,1)\) 的子矩形翻转,代价为 \(1\)。
- 选择一个包含 \((n,1)\) 的子矩形翻转,代价为 \(2\)。
- 选择一个包含 \((1,m)\) 的子矩形翻转,代价为 \(4\)。
- 选择一个包含 \((n,m)\) 的子矩形翻转,代价为 \(3\)。
初始矩阵全 \(0\),问最少代价使得变成目标矩阵。
\(n,m\le 500\)。
标签:贪心,构造。
草,随便一道 *2600 我都不会了。
首先 \((1,m)\) 和 \((n,1)\) 操作显然无用,因为可以用两次 \((1,1)\) 操作代替掉。
所以只需要考虑两个操作,不会了,看题解。
考虑一次操作的变化量,令 \(b_{i,j}\) 表示 \(a_{i,j},a_{i,j+1},a_{i+1,j},a_{i+1,j+1}\) 的异或和,这样的话可以发现 \((1,1)\) 操作本质上修改了一个 \(b_{i,j}\) ,\((n,m)\) 操作修改了 \(b_{i-1,j-1},b_{i-1,m},b_{n,j-1},b_{n,m}\) 的值。
所以先统计 \(b_{i,j}\) 的和,然后看看是否可以用一个 \((n,m)\) 操作代替四个 \((1,1)\) 操作即可。
ARC070F *3365 \(\color{Gold}\bigstar\)
交互题,有 \(A\) 个好人和 \(B\) 个坏人,每次询问 \(x\),\(y\) 是不是好人,好人说真话,坏人随机说真话或者假话,在 \(2n\) 次询问后确定每个人的身份。
\(A,B\le 2000\)。
标签:构造。
考虑如果 \(A\le B\) 那么显然无解,因为可以选择 \(A\) 个坏人假装是好人,然后然后和好人没有区别,无法分辨。
否则,考虑一个询问如果是对方是坏人,那么两个人之间至少有一个坏人,可以把两个人都扔掉,因为好人人多,最后可以剩下好人。
如果知道一个好人,再通过 \(n\) 次询问即可。
具体而言,维护一个栈,每次问栈顶外面的一个人是否是好人,如果否就弹栈,两个人都扔掉,否则入栈,可以发现这样最后栈一定是栈顶一堆好人,栈底一些坏人,因为好人后面不可能有坏人。
所以找到栈顶即可。
P6047 \(\color{green}\bigstar\)
题比较长,自己看吧。
标签:斜率优化 dp。
考虑如果两条线相交,那么只需要保留 \(v\) 更小的,所以变成一堆不相交的先,就可以直接处理 \(a,b\) 的前缀后缀最小值,然后 dp,\(f_i\) 表示前 \(i\) 条线满足的最小值,先写一个暴力式子,然后一眼斜率优化就做完了。
CF1373G *2600 \(\color{gold}\bigstar\)
\(n\times n\) 的棋盘上,第 \(k\) 行是特殊行,\((x,y)\) 表示第 \(x\) 行,第 \(y\) 列,这个位置的兵可以走到 \((x-1,y+1),(x,y+1),(x+1,y+1)\)。
每个兵都要走到第 \(k\) 行,不能有两个兵重合,可以在棋盘后添加若干列让每个兵都能走到第 \(k\) 行。
初始状态没有兵在棋盘上,现在有 \(m\) 个操作,将 \((x,y)\) 的状态改变,有兵则拿掉,没兵则添加。求每次操作后求需要最少要添加几列。
标签:线段树。
开始口胡了一个很阿拉丁的做法,首先显然,一个兵 \((x,y)\) 到 \(k\) 的横坐标最小为 \(y+|k-x|\),但这样可能会有重复,所以要向后移动。
考虑加入一个数就直接在后面找第一个空的位置放进去,这个找空位可以直接并查集,但删除比较恶心。
所以显然可以线段树分治。。。时间复杂度 \(O(n\log^2 n)\),不知道能不能过。
考虑另外的做法,每次删除必然删除当前点向后走的最右边的点,这样显然最优。
因此考虑设 \(f_i\) 表示兵在第 \(k\) 行向右走时经过了 \((k,i)\) 点 \(f_i\) 次,那么加点相当于就是找第一个 \(f_i=0\) 的点,删除就是找第一个 \(f_i=1\),然后就是区间加减,显然可以线段树二分做,时间复杂度 \(O(n\log n)\)。
AGC017C *3133 \(\color{gold}\bigstar\)
\(N\) 个球排在一起,每个球上有一个数 \(a_i\)。接下来会进行若干轮删除。设现在还有 \(k\) 个球,则 \(a_i=k\) 的球会被删除。
最终可能球不会被删完,你需要求出最少修改几个球上的数后可以让球全部被删完。
同时还有 \(M\) 次修改,每次修改第 \(X_i\) 个球的数为 \(Y_i\),你需要求出每次修改后上述问题的答案。
标签:贪心。
牛子题。
考虑全部删完需要什么条件,随便推一下就可以发现本质是向下面这张图(贺的)。
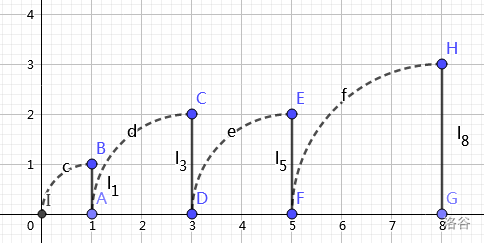
线段横坐标表示数值,纵坐标表示出现次数,可以清空的条件就是放倒后可以到达前一条线段处。
考虑第一次答案咋算,显然线段高度可以开桶预处理。
如果一条线段覆盖了另一个点,像下面这个:
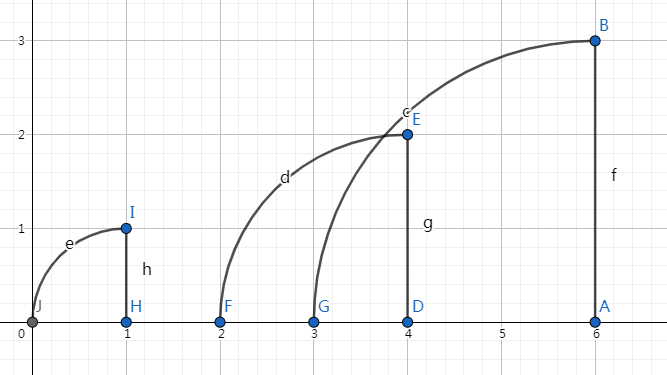
那么最优方案显然是 \(AB\) 缩短一格,然后 \(ED\) 增加一格。
所以把线段放倒,记录一下 \(x\) 坐标轴上每个点被覆盖多少次 \(s_i\)。
答案就是 \(\sum \max(s_i-1,0)\)。
线段会倒到负半轴,比较难搞,所以可以统计 \(0\) 的个数。
这样就得到了初始的答案。
那么修改就是相当于修改两条线段长度,直接修改就好了。
CF1140G *2700 \(\color{green}\bigstar\)
题比较长,自己看吧。
标签:倍增。
先对同构的两点距离进行处理,可能可以绕一圈更优。
然后就可以发现走的必然是一条最短最短路径,可以记录一下再两个树上分别的最短路径,然后就可以每次前进一步,看看是否要在两颗树中间跳。
这样复杂度显然爆炸,容易发现这个东西可以动态 dp,但我不想写。
可以发现这个向上爬的过程是可以倍增优化,预处理一下然后倍增跳就好了。
时间复杂度 \(O(n\log n)\),但代码是真的阿拉丁。
P5384 \(\color{blue}\bigstar\)
给一棵树,\(Q\) 次询问求一个点的 \(k\) 级祖先的 \(k\) 级儿子有多少个。
\(n,Q\le 10^6\)。
标签:桶,树。
本题有一堆单 \(\log\) 做法,好像都会被卡。
考虑查询 \(k\) 级祖先可以离线,开一个栈维护一个点的祖先就可以直接查询。
子树内一个深度的点的个数可以考虑开桶,在进入子树前统计该深度点数量,然后离开子树时在做两者之差即可。
时间复杂度 \(O(n+Q)\),这个做法还是很妙的。
离线部分如果用 vector 实现会 MLE,需要用链表。
P1600 \(\color{green}\bigstar\)
题比较长,自己看吧。
标签:桶,树。
可以发现一个人的跑步分为上升和下降两部分,上升时深度与时间和为定值,下降则两者只差为定值,那么就可以分别开桶记录。
进行树上差分之后相当于子树中一个值之和,那么就和上题做法一样,在进入子树前后分别记录就好了。
CF1617E \(\color{Gold}\bigstar\)
有 \(n\) 个数组,每个数组选择一半扔到一个集合,另一半扔到另一个集合,是两个可重集相等,构造方案。
标签:构造。
两个条件,考虑都去满足。
一个构造方案是一个数组中的点分奇偶性相邻连边,然后一个数与这个数上一次出现的位置连边,如果图是二分图,那么合法。
由于两种边各连一条,所以必然是二分图,直接染色即可。
还不是很悟到,先咕着。
CF1458C *2700 \(\color{blue} \bigstar\)
给一个矩阵,每行每列都是一个排列,有六种操作,四种是向四个方向循环平移一格,还有两种分别是对每一行或者每一列的排列进行逆排列变换,求操作 \(m\) 次后的矩阵。
\(n\le 1000,m\le 10^5\)。
标签:矩阵。(?其实好像没啥标签好评的。
不是很难,但我想了好久(。
先考虑只有行咋做,逆排列本质上是把函数上的横纵坐标交换,所以说只需要开两个数组来记录每个点的横纵坐标,逆排列就是交换,否则就是全局加,可以记录一下。
现在有了行列,那么就用三维记录一个点,逆排列还是相当于交换两个数组,直接做就好了。
CF1149C *2700 \(\color{Gold} \bigstar\)
给一个长度为 \(2(n-1)\) 的括号串,对括号串建树,有 \(m\) 交换两个括号操作,求每次操作后括号树的直径,保证每次操作后的括号串合法。
\(n,m\le 10^5\)。
标签:线段树。
考虑左括号就是向下一步,右括号就是回去一步,那么一段区间去掉所有匹配括号后就会变成 ))))((( 的形式,这样就代表一条树上的链,长度为该括号串长度。
假设区间是 \([l+1,r]\),中间分隔点是 \(k\),记录前缀括号和是 \(s_i\),那么左边右括号的个数就是 \(s_l-s_k\),右边左括号个数就是 \(s_r-s_k\),也就是相当于维护 \(s_l+s_r-2s_k\) 的最大值。
比较经典,维护 \(s_l,-2s_k,s_l-2s_k,s_r-2s_k,s_l+s_r-2s_k\) 的最大值,区间可以直接合并,用线段树轻松维护。
CF1667E *3000 \(\color{red}\bigstar\)
有 \(n\) 个点( \(n\) 为奇数),第 \(i\) 个点与一个满足 \(j<i\) 的点连边,最后形成一棵树,求对于每个 \(1\le i\le n\) 求出 \(i\) 为重心的树的数量,对 \(998244353\) 取模。
标签:组合数学,容斥,多项式。
神题。
首先以 \(1\) 为根,这样一个点的子树中的点编号一定大于该点。
然后可以发现如果 \(i\) 子树大小至少是 \(\frac{n+1}{2}\),不然子树外的点数就不满足重心了,记 \(S=\frac{n+1}{2}\)
令 \(f_i\) 表示 \(i\) 子树大小至少是 \(S\) 的方案数,那么可以得到:
这个式子咋理解呢,可以发现 \(n\) 个点的树有 \((n-1)!\) 棵,且根一定是编号最小的那个,所以直接在后面选 \(j\) 个,然后和 \(i\) 形成一棵子树,然后剩下的点就形成一棵树,然后 \(i\) 可以选择接在、哪个点后面。
这个东西显然可以整理之后使用 NTT 计算。
然后考虑答案,设 \(g_i\) 表示 \(i\) 号点的答案,那么首先显然需要满足 \(f_i\) 的条件,那么然后如果不是重心,说明重心一定在 \(i\) 的子树中,可以得到:
为啥要除以 \(i\) ?,因为 \(j\) 可能不在 \(i\) 的子树中,在 \([1..i]\) 中都有可能,且概率等价,所以除以掉。
然后就可以 \(O(n\log n)\) 直接计算了。
\(\color{red}{Swistakk}\):FFT in E? I believe I solved it in much easier way.
是的,上面的多项式做法被怒斥了,这位 IGM 选手提出了吊打 std 不知道多少的优秀组合解法。
事实上:
然后就不需要上面的 NTT 了。
考虑先把 \([1,i]\) 的点都按顺序放好,然后考虑对于 \(>i\) 的点就选择一个 \([1,i]\) 的点,然后插入到它的后面,表示在它的子树内。
然后可以发现满足条件实际上就是要求 \(i\) 在前 \(S-1\) 个位置内,也就是 \([1,i]\) 都需要在前 \(S-1\) 个位置内。
考虑只放这 \(i\) 个数,算出概率后乘上总方案即可,\(1\) 必然在第一个位置,所以相当于放 \(i-1\) 个数,然后就得到了上面的式子。
直接算就好了,时间复杂度 \(O(n)\)。
ARC116D *1718 \(\color{green}\bigstar\)
问有多少个长度为 \(n\) 的非负整数序列满足 \(\sum a_i=m\),且异或和为 \(0\)。
\(n\le 5000\)。
标签:dp
容易想到一个 dp,\(f_{i,j}\) 表示到了第 \(i\) 位,和为 \(j\) 的方案数,可以直接枚举这一位有多少个 \(1\) 来转移,时间复杂度 \(O(n^2\log n)\)。
此题有一个更加有趣的做法,考虑每次选择一位上选几个,然后把所有数都乘 \(2\),这样显然满足要求,而且和上面的本质相同,记 \(f_i\) 表示和为 \(i\) 的答案,那么就可以得到:
时间复杂度变成 \(O(n^2)\),吊打前面的做法。
ARC112E *2659 \(\color{blue}\bigstar\)
开始有一个序列长度为 \(n\) 的序列 \(a_i=i\),每次操作可以选择一个点移动到最前面或者最后面,进行 \(m\) 次操作后变成目标序列,求操作方案数,对 \(998244353\) 取模。
\(n,m\le 3000\)。
标签:组合数学,容斥。
想了半天推出来了,好题。
考虑如果一个数被操作了,那么最后的位置只与它最后一次操作的位置有关。
设 \(f_i\) 表示对 \(i\) 个数进行 \(m\) 次操作,最后一次操作确定左右且顺序一定的方案数,可以直接容斥得到:
直接 \(O(n^2)\) 计算,然后考虑如果一些数没有被操作,那么最后必然形成一段在中间的区间,而且满足单调递增,所以可以直接枚举区间,那么就相当于左边放 \(x\) 个数,右边 \(y\) 个数的方案数。
确定一下最后一次操作左右的顺序可以得到该部分的贡献是 \(\binom{x+y}{x}f_{x+y}\)
还有可能所有数都操作的情况,那就枚举那个数最先放入,然后再左右分别放,由于第一个放入的数可以从左或者右放入,方案数乘 \(2\)。
ARC128D *2554 \(\color{Gold}\bigstar\)
有 \(n\) 个数,每次可以选择相邻的三个数 \(x,y,z\),然后如果满足 \(x\ne y,y\ne z\),那么就可以把 \(y\) 删除,\(x,z\) 就变相邻,求若干次操作之后有多少种可能的序列,对 \(998244353\) 取模。
\(n\le 2\times 10^5\)。
考虑怎样的区间是可以被删除的。
如果一个区间中有两个相同的数相邻,那么显然无法删除。
否则相邻两个都不一样,考虑不合法一定是无论怎么删都会出现相邻两个一样,那么考虑出现相邻两个一样的前一步,必然保证是 \(01010101...\) 这样的形式,不然可以再删一步,所以只需要判断这样交错的形式即可。
设 \(f_i\) 表示 \(i\) 是最后一个保留数的方案数,第一个限制可以直接维护相同的位置用前缀和处理,后面的可以记录一个需要减去的 \(f_j\) 值之和即可。
ARC128D *2554 \(\color{Gold}\bigstar\)
有 \(n\) 个数,每次可以选择相邻的三个数 \(x,y,z\),然后如果满足 \(x\ne y,y\ne z\),那么就可以把 \(y\) 删除,\(x,z\) 就变相邻,求若干次操作之后有多少种可能的序列,对 \(998244353\) 取模。
\(n\le 2\times 10^5\)。
标签:dp。
考虑怎样的区间是可以被删除的。
如果一个区间中有两个相同的数相邻,那么显然无法删除。
否则相邻两个都不一样,考虑不合法一定是无论怎么删都会出现相邻两个一样,那么考虑出现相邻两个一样的前一步,必然保证是 \(01010101...\) 这样的形式,不然可以再删一步,所以只需要判断这样交错的形式即可。
设 \(f_i\) 表示 \(i\) 是最后一个保留数的方案数,第一个限制可以直接维护相同的位置用前缀和处理,后面的可以记录一个需要减去的 \(f_j\) 值之和即可。
JOI2018C \(\color{Gold}\bigstar\)
有一个 \(n\times m\) 的矩阵,每个格子有一个颜色,每次可以选择从左到右连续的或者从上到下连续的三个
RGW并取走这三个字母,问最多可以操作多少次。
\(n,m\le 3000\)。
标签:dp。
用中间的 \(G\) 来表示一个操作的位置,考虑怎样的操作会相互影响,可以发现只有 \((x,y)\) 和 \((x-1,y+1)\) 这样的两个格子会相互影响,其他情况要么互不影响,要么必然有一个不满足 RGW 的条件。
所以就可以一条条对角线进行 dp,记录当前是竖的还是横的即可,时间复杂度 \(O(n^2)\)。
CF455D *2700 \(\color{gray}\bigstar\)
有 \(n\) 个数,两种操作,区间循环移位一格,区间查询一个数出现次数,强制在线。
\(n\le 10^5\)。
标签:分块。
简单题,显然分块一下,然后每个块开一个双端队列,再开桶记录每个数出现次数,修改就相当于双端队列弹出一个加入一个,两边散块暴力维护即可。
时间复杂度 \(O(n\sqrt{n})\)。
CF713D *2700 \(\color{gray}\bigstar\)
给一个 \(n\times m\) 的 \(01\) 矩阵,每次询问一个子矩阵内,全为 \(1\) 的正方形的边长最大值。
\(n\le 1000\)。
标签:dp,st 表。
先跑一遍 dp,求出 \(f_{i,j}\) 表示以 \((i,j)\) 为右下角的正方形最大边长。
显然可以二分答案一下,然后相当于询问一个子矩阵最大值,直接 st 表维护即可。

