3月杂题选做(part 1)
关于难度
\(\color{gray}\bigstar\) 可以秒杀的题。
\(\color{green}\bigstar\) 思考一会儿后可以秒的题。
\(\color{blue}\bigstar\) 需要较长时间思考的题。
\(\color{Gold}\bigstar\) 看题解、稍加指点就会做的题。
\(\color{red}\bigstar\) 看题解后需要较长时间消化,甚至现在都没有完全理解的题。
本月主要板刷 cf *2300~*2400 的题。
一些简单的 DS 题就直接嘴巴了。
由于博客过长会导致 markdown 加载缓慢,所以源码长度超过 \(1000\) 行时进行分 P 处理。
CF1468M *2300 \(\color{Gold}\bigstar\)
已知 \(n\) 个集合,问是否存在两个集合满足这两个集合的交集大小大于等于 \(2\)。
\(1\le n\le 10^5\)。
标签:根号分治。
显然可以对每个数字考虑,把包含这个数字的集合彼此连边,有两条边的就有了答案。
但是必须满足直接连边,比较难维护。
考虑根号分治。
令 \(m=\sum |S_i|\)。
如果序列长度大于 \(\sqrt{m}\),那么就暴力扫其他序列看交集是否大于 \(2\)。
如果小于 \(\sqrt{m}\),那么直接考虑 \(|S|^2\) 暴力求出每一对数,然后只需要判断是否出现两次就好了,容易证明总复杂度为\(m\sqrt{m}\)。
注意后者判是否相等如果用 map 会多一个 log,TLE,所以需要存下来离线判断。
CF1625D *2300 \(\color{green}\bigstar\)
已知 \(n\) 个数,问从中最多选出多少个数,使得任意两数异或结果大于等于 \(k\),输出方案。
\(1\le n\le 3\times 10^5\)
标签:trie 树,贪心。
位运算题先考虑 trie 树。
考虑如果两数异或的结果在 \(k\) 的最大位前面有 \(1\),那么一定满足要求。
所以相当于 trie 深度小于 \(k\) 最高位的可以随便走,大于的可以发现实际上就是一堆子树,每个子树要么选一个,要么选两个。
上面的结论可以用鸽巢原理,如果选三个,那么 \(k\) 的最高位就变成了 \(0\),不合法。
考虑每棵子树咋算。
贪心,对 \(a_i\) 排序后从小到大放入 trie,看看子树中是否存在另一个数满足异或结果大于等于 \(k\)。
CF856D *2400 \(\color{blue}\bigstar\)
已知一棵树和 \(m\) 条边,你可以选择若干条边加入,使得原树变成一个仙人掌,选择一条边有一个价值,求价值之和最大是多少。
仙人掌指每个点最多属于一个环。
\(1\le n,m\le 2\times 10^5\)
标签:树形 dp。
考虑加边本质上就是让一条链上的点删掉,因为它们不能与其他边构成环。
考虑 dp,设 \(f_i\) 表示以 \(i\) 为根的子树的答案。
然后一条边就考虑在两个点的 LCA 处更新答案。
令 \(g_i=\sum f_{son}-f_i\)。
然后可以发现一条边的贡献实际上就是一条链查询和。
树剖可以 \(O(n\log^2 n)\),也可以直接考虑链上的点会对子树中的查询产生贡献,所以树状数组维护子树修改就可以 \(O(n\log n)\)。
CF1436E *2400 \(\color{green}\bigstar\)
求一个数列的所有连续子数列的 mex 值的 mex。
标签:线段树,莫队
一个简单的思路是对于每个 \(x\),判断是否存在一个连续子序列满足它的 mex 值等于 \(x\)。
一个子序列满足的条件是不能出现 \(x\),要出现 \(1...x-1\) 中的所有数。
可以根据每个出现的 \(x\) 把序列分成若干块,只需要查询每一块是否出现了 \(1...x-1\) 就好了。
这个显然可以离线莫队,时间复杂度 \(O(n\sqrt{n})\)。
也可以建值域线段树,每个点表示该值出现最右边的位置,查询时只需要查询区间最小值即可,复杂度 \(O(n\log n)\)。
CF1630D *2400 \(\color{Gold}\bigstar\)
已知一个长度为 \(n\) 的序列 \(A\),一个长度为 \(m\) 的序列 \(B\),每次操作选择一个 \(b_i\),将 \(A\) 中一段长度为 \(b_i\) 的区间中的数变成它们的相反数,求 \(\sum a_i\) 的最大值。
\(n\le 10^6,m,b_i\le \frac{n}{2}\)
标签:贪心。
由于是反转操作,所以一个 \(b_i\) 操作后再操作一个 \(b_j\) 相当于操作了一个 \(b_i-b_j\),可以用辗转相减法证明最小操作长度为 $G=\gcd ( b_1,b_2...b_m ) $,那么题意转化为每次操作一个长度为 \(G\) 的区间。
对 \(i\mod G\) 的值进行分组,那么发现每次操作会让每组中的一个数变成相反数。
所以每组操作次数都是相同的。
由于是反转操作,操作次数只需要注意其奇偶性,因为多出来的操作可以一直操作一个数。
枚举其奇偶性,然后贪心操作每组就好了。
CF1619H *2400 \(\color{Gold}\bigstar\)
已知一个长度为 \(n\) 的排列 \(p\),操作一次 \(x\) 会使 \(x=p_x\),有 \(m\) 个操作,需要维护两种操作:
1 x y交换 \(p_x,p_y\)。
2 x y查询 \(x\) 进行 \(y\) 次操作后的结果。
\(1\le n,m\le 10^5\)。
标签:分块,根号分治。
首先 \(p\) 是个排列所以一定可以构成一个置换环,考虑在环上跳 \(y\) 步如何维护。
如果没有交换,显然可以倍增跳,但有修改难以维护。
分块一下,令 \(B=\sqrt{n}\),记录 \(Nex_i\) 表示 \(i\) 操作 \(B\) 次的结果。
每次修改最多只会修改 \(\sqrt{n}\) 个 \(Nex_i\),直接暴力维护就好了。
时间复杂度 \(O(m\sqrt{n})\)。
CF1609E *2400 \(\color{blue}\bigstar\)
给你一个长为 \(n\) 的字符串,只包含
abc三种字符。\(Q\) 次操作,每次把一个位置的字符改成给定字符,询问当前串至少修改几次满足不包含子序列abc。修改指把一个位置的字符修改成 \(a,b,c\) 三种字符之一。
\(1\le n,Q\le 10^5\)。
标签:线段树。
既然已知目标字符串 a,b,c,那么可以暴力设出状态 \(f_S\) 表示不含子串 \(S\) 的最小操作次数。
考虑如何在线段树上进行合并。
如果 \(|S|=1\),显然左边加上右边就好了。
对于 \(S=ab,bc,abc\),大力讨论一下,可以推出式子。
\(L,R\) 表示左右儿子的 \(f\) 值。
线段树维护一下就好了,时间复杂度 \(O(Q\log n)\)。
code。
CF1598F *2400 \(\color{green}\bigstar\)
已知 \(n\) 个括号序列,你可以对它们进行排序,使得顺次首尾相接之后前缀合法括号序列数最大,求这个最大值。
\(1\le n\le 20,1\le \sum |S|\le 4\times 10^5\)。
标签:状压 dp。
\(n\le 20\) 一眼状压。
设 \(f_S\) 表示选了串集合为 \(S\) 的答案。
括号序列有一个经典的转化,左括号加一,右括号减一,合法括号序列要求不能有一个前缀小于零。
记录 \(cnt_S\) 表示选了 \(S\) 前缀值是多少。
考虑后面接上一个串 \(s_i\),令 \(mn_i\) 表示 \(s_i\) 的最小前缀,\(sum_i\) 表示最小前缀的出现次数。
如果 \(cnt_S+mn_i> 0\) 那么加上后合法,对答案不会产生任何贡献。
如果 \(cnt_S+mn_i=0\) 那么加上后合法,对答案产生 \(sum_i\) 的贡献。
如果 \(cnt_S+mn_i<0\) 那么加上后就寄了,所以需要直接更新最后答案,这个串对答案的贡献可以开始时预处理一下。
时间复杂度 \(O(2^n+\sum |S|)\)。
code。
CF1585E *2400 \(\color{green}\bigstar\)
已知一颗树,点有点权,有 \(Q\) 次询问,每次询问给出三个数 \(v,l,k\),表示查询在 \(v\) 到 \(1\) 号点路径上的点权写下来,写成一个序列,按每个数字的出现次数排序,把出现次数小于 \(l\) 的去掉,然后查询第 \(k\) 的数。
\(1\le n,q\le 10^6\)。
标签:线段树二分。
一个简单的想法是直接离线一下,做 dfs 的路径上统计每个数字出现次数,考虑如何维护。
建一棵线段树,下标表示出现次数,那么直接查询第 \(k\) 大即可,输出方案的话可以直接在节点上开 set 统计。
直接线段树上二分,时间复杂度 \(O(Q\log n)\)。
官方题解是 \(O(n+Q)\) 的,可惜我看不大懂。
CF1237E *2400 \(\color{red}\bigstar\)
有多少棵点数为\(n\),点权为 \(1,2,...,n\) 中的数的二叉搜索树满足:
- 除了最下面一层外,所有层都是满的;
- 对于每个点,如果它有左儿子,那么左儿子的点权和它的奇偶性不同;如果它有右儿子,那么右儿子的点权和它的奇偶性相同。
答案对\(998244353\)取模。
\(1\le n\le 10^6\)。
标签:构造。
神仙题。
手玩一下小数据,可以发现深度小于等于 \(3\) 的只有树大小为 \(1,2,4,5\) 四种情况,并且方案数都是 \(1\)。
显然,由于是平衡树,那么 \(n\) 显然是根一直向右走到的点,可以发现必然与根节点奇偶性相同,所以右子树大小是偶数。
可以发现,一棵满足条件的树,它的左右子树也都必然满足条件。
所以可以从深度小的向深度大的递推。
设 \(f_i\) 表示深度为 \(i\) 的满足条件的平衡树的最小大小。
用归纳法证明只有大小为 \(f_i,f_i+1\) 的树可以满足条件。
首先对 \(i=1,2\) 显然成立。
假设对于 \(i\) 成立,那么深度为 \(i+1\) 的树必然是一个根再加上两个深度为 \(i\) 的树。
深度为 \(i\) 的树只有 \(f_i,f_i+1\) 两种。
设左右两子树大小为 \(L,R\),那么需要满足 \(L+1\) 和 \(L+R+1\) 奇偶性相同。
所以 \(R\) 必然是偶数,\(L\) 可以取 \(f_i\) 和 \(f_i+1\)。
这样证明了上面的结论,也证明了方案数只可能是 \(0,1\)。
递推式也很简单:
code。
CF1106F *2400 \(\color{Gold}\bigstar\)
已知一个长度为 \(k\) 的序列 \(b\),有一个序列 \(f\) 满足在 \(i>k\) 时:
已知 \(f_1=f_2=f_3=...f_{k-1}=1,f_n=m\),求 \(f_k\)。
\(k\le 100,n\le 10^9\)。
标签:数论,矩阵,原根。
比较好的数论题,借此复习一下数论。
上面的式子中全都是乘法,而且有取模,很不好处理。
可以发现 \(998244353\) 有一个知名的性质:原根是 \(3\)。
而原根正好可以把乘法变成加法,方便运算。
设 \(3^{g_i}=f_i\),显然 \(g_1=g_2=...g_{k-1}=0\)。
式子变成 \(g_i=\sum_{j-1}^k g_{i-j}^{b_j} \mod 998244352\)。
如果已知 \(g_k\) 去推 \(g_n\) 那很好做,直接矩阵快速幂即可。
转移矩阵长这样:
就是主对角线下面的对角线上都是 \(1\)。
初始向量是 \(B=[0,0,0...g_k]\)。
求出来的就是
后面那个可以先算,而 \(B\) 前面的都没有用,所以可以惊人地发现 \(g_n\equiv g_k\times A_{k,k} \pmod {998244352}\)。
求个逆元就好了,注意模数非质数,需要用 exgcd。
CF906C *2400 \(\color{green}\bigstar\)
一共 \(n\) 个人,给你 \(m\) 对的关系,然后每一个关系对代表两个人认识。然后你每次可以选择一个人 \(i\),让 \(i\) 认识的所有人都相互认识,然后现在问你最少需要选择多少个这样的 \(i\),使得所有的人都相互认识。
\(1\le n\le 22\)。
标签:状压 dp。
比较套路的题吧,设 \(f_i\) 表示集合 \(i\) 的人互相认识的最小次数,然后枚举一下下一步操作那个就好了。
轻微卡常,枚举时用 lowbit 优化一下,时间复杂度 \(n\times 2^{n-1}\)。
注意特判开始就合法的答案。
CF342E *2400 \(\color{blue}\bigstar\)
给定一棵 \(n\) 个节点的树,初始时 \(1\) 号节点为红色,其余为蓝色。
要求支持 \(Q\) 次如下操作:
- 将一个节点变为红色。
- 询问节点 \(u\) 到最近红色节点的距离。
\(1\le n,q\le 10^5\)。
标签:分块。
考虑暴力咋做。
两种方法,一种是枚举红点,一种是从红点开始 BFS。
两种做法各有优势,考虑综合起来。
类似于二进制分组,考虑对操作分块一下。
对于前面整块的,用后面的方法,对散块用前面的暴力。
注意求 \(LCA\) 用 st 表做,否则带 log。
总时间复杂度 \(O(n\sqrt{q})\)。
CF865D *2400 \(\color{Gold}\bigstar\)
已知接下来 \(n\) 天的股票价格,每天可以选择买入一股或者卖出一股,初始钱无限,问最多赚多少钱。
\(n\le 3\times 10^5\)。
标签:反悔贪心。
一开始已知在想 dp,然后一直想不出来。
其实知道是贪心后就挺简单了。
一个很 naive 的贪心是,每次找前面没取过的最小的一个,看看当前的是否大于前面的,如果大于就拿。
这样会有一个问题,贺一组洛谷上的 hack:
3
1 2 100
如果先把 \(1,2\) 取了,\(100\) 就没地方取了。
所以对于已经卖出的开一个堆,看看是否有比自己小的,如果小了就把它替换出来。
CF1083E *2400 \(\color{green}\bigstar\)
已知 \(n\) 个矩形,左下角都是坐标 \((0,0)\),右上角是 \((x_i,y_i)\),满足没有任意两个矩阵有包含关系,矩形都有一个代价 \(a_i\),现在可以选出若干个矩形,问矩形面积并减去代价之和最大是多少。
\(n\le 10^6,x_i,y_i\le 10^9\)。
标签:斜率优化 dp。
这题挺简单的,不知道为啥 *2400。
由于没有包含关系,所以矩形长这样:
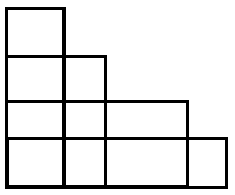
显然从左向右考虑,假设我们当前选择了一个矩形,考虑多出来的面积。
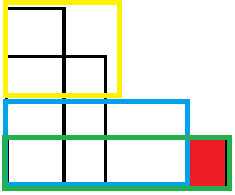
绿色框是当前选的矩形,蓝色是上一个选的矩形,红色部分便是多出来的面积。
可以发现,这个面积和再之前选的(即黄色部分)矩形没有关系。
选择一个矩形增加的面积只与上一个矩形有关,显然可以考虑 dp。
设 \(f_i\) 表示最后一个选的是 \(i\) 的答案最大值。
暴力做 \(O(n^2)\),这个式子显然可以斜率优化,斜率式子:
单调队列维护,没了。
CF145E *2400 \(\color{gray}\bigstar\)
给你 \(n\) 个数,每个数是 \(4\) 或者 \(7\) ,给你 \(m\) 个任务完成。
switch l r把 \([l,r]\) 位置的 \(4\) 换成 \(7\) , \(7\) 换成 \(4\)。
count计算 \(n\) 个数的最长不下降子序列的长度。
标签:线段树。
简单题,直接线段树无脑维护区间 \(4,7\) 个数,和不上升,不下降的长度,修改直接交换,合并也很简单。
CF739C *2500 \(\color{green}\bigstar\)
现在有 \(n\) 个数,\(m\)个操作,每次区间加一个数,对于每一次操作,你要找出最长的\(a_l...a_r\),满足
输出其长度。
有一个无脑做法,维护左右的单调下降的有多长,直接合并就好了,这里不讲。
来个巧妙的不需要 lazytag 的做法。
考虑差分,这样的话查询就相当于移动与正数然后一堆负数,修改只需要修改两个数,维护一下左右的答案,直接合并就好了。
CF444C *2400 \(\color{gray}\bigstar\)
有一个 \(n\) 个元素组成的序列,每个元素有两个属性:颜色 \(c_i\) 和权值 \(w_i\) 。\(c_i\) 初始为 \(i\),\(w_i\) 初始为 \(0\)。\(m\) 次操作,操作有两种:
1 l r x:对 \(i\in [l,r]\) 的所有 \(i\) 进行如下操作:设第 \(i\) 个元素 原来 的颜色为 \(y\),您要把第 \(i\) 个元素的颜色改为 \(x\),权值 增加 \(|y-x|\)。2 l r:求 \(\displaystyle\sum_{i=l}^r w_i\) 。
标签:线段树。
没啥好说的,区间推平,直接记录一下是否被推平,如果已经被推平就退出,否则暴力递归就好了。
可以证明递归次数是 \(O(n+m)\) 级别的。
CF446C *2400 \(\color{Gold}\bigstar\)
在本题中,我们用 \(f_i\) 来表示第 \(i\) 个斐波那契数 ,\(f_1=f_2=1,f_i=f_{i-1}+f_{i-2}(i\ge 3)\)。
维护一个长度为 \(n\) 的序列 \(a\),有 \(m\) 次操作:
1 l r:对于 \(l\le i\le r\),将 \(a_i\) 加上 \(f_{i-l+1}\)。2 l r:求 \(\displaystyle\left(\sum_{i=l}^ra_i\right)\bmod(10^9+9)\)。
\(1\le n,m\le 3\times 10^5,a_i\le 10^9\)。
标签:数学,线段树。
同样是 *2400 差别咋就那么大呢。
一开始我的想法是差分一下,\(c_i=a_i-a_{i-1}-a_{i-2}\),这样修改很容易但查询不会,寄。
考虑每个数加上 \(f_{i-l+1}\),研究一下性质。
\(f_{n+m}=f_nf_{m+1}+f_{n-1}f_m\),这个结论可以归纳法证。
对 \(n=1,2\) 时显然成立,然后只需要把 \(f_{m+1}\) 拆成 \(f_m+f_{m-1}\) 就可以证明了。
然后拆 \(f_{i-l+1}=f_if_{2-l}+f_{i-1}f_{1-l}\)。
可以发现相当于区间上进行一个操作,且对于每个数操作都相同,就可以区间维护了。
具体来说维护区间 \(f_i,f_{i-1}\) 的和,这个可以预处理,每次操作直接区间加就好了。
CF1082G *2400 \(\color{Gold}\bigstar\)
定义图权 = 图中边权总和 − 图中点权总和,求 \(n\) 个点 \(m\) 条边的无向图最大权子图。
标签:网络流。
本题同 [NOI2006] 最大获利,好像是个模板?
考虑网络流,选一条边的前提是需要选两个点。
这就是一个限制条件,要么选边,点也需要选,要么边不选。
考虑最小割,矛盾条件是不选点,但选了边,在此时源点汇点要联通。
构造一下,将每条边建一个点,得到这样的建边方式:
-
源点向每个点连边,边权为该点点权。
-
每个点向自己所连连的边连边,边权为 Inf 。
-
每条边向汇点连边,边权为该边边权。
这样答案就只需要将所有边权加起来减去最小割就可以了。
CF1401E *2400 \(\color{blue}\bigstar\)
给定一个\(10^6\times 10^6\)的正方形,\(n\) 条横线和 \(m\) 条竖线穿过了它,求这些线把正方形分成了多少个部分。
注意: 每条线的两个端点之一一定在正方形的边上。
标签:树状数组。
开始一看这题:这不 sb 题,每个部分都在最右边统计一下,横线就在树状数组上修改,竖线就查询区间和。
结果发现萎掉了。
因为左边不一定被分成两个部分,会出现:
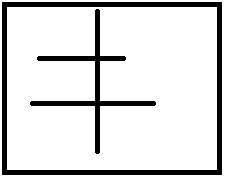 ]
]
这个图只有一个部分,中间那个却会被算上。
想了好久,发现题目看错了,至少有一端是靠墙的。
考虑对每条竖线考虑,以碰上边为例
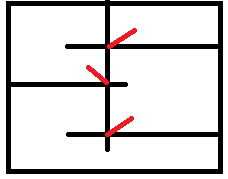
可以发现,划分出的区域可以与交点一一对应。
一个例外是上下都碰,区域会多一个。
所以答案就是内部交点个数 + 长度为 \(10^6\) 线段个数 + \(1\)。
显然可以直接树状数组一样,实现起来和最前面的假做法一模一样,只需要加个长度为 \(10^6\) 的特判就好了。
CF1340C *2400 \(\color{gray}\bigstar\)
有一个数轴, \([0,n]\) 范围内的每个整点是一个路口。
其中有 \(m\) 个特殊的路口,记作 \(d_1,d_2,\cdots,d_m\),在这些路口有安全岛。
Denis 从 \(0\) 号路口出发,每秒钟可以从第 \(x\) 个路口移动到第 \(x-1\) 或者第 \(x+1\) 号路口,他只能在安全岛改变移动方向。
有一个红绿灯,绿灯时间为 \(g\) 秒,红灯时间为 \(r\) 秒, Denis 在绿灯时间内必须移动,在红灯时间内必须在某个安全岛停留。他出发的时候红绿灯刚从红灯变为绿灯。
求 Denis 到达 \(n\) 号路口的最短时间。
\(n\le 10^6,g,r\le 1000,m\le 10000\)
标签:BFS。
这样也能 *2400?这 *800 差不多得了。
直接分层图,\(f_{i,j}\) 表示到了 \(d_i\),这个绿灯还有 \(j\) 时间的最短路。
实际上边权只有 \(0\) 和 \(1\) ,因为 \(g\) 时间一个阶段。
点很少, \(10^7\) 个,跑 01-BFS,没了。
CF815C *2400 \(\color{gray}\bigstar\)
有 \(n\) 个物品,每个物品有价格 \(w_i\),每个物品可以使用优惠券使价格减少 \(d_i\),但如果 \(i\ge 2\) 使用了优惠券,就需要保证第 \(x_i\) 个物品必须买,你现在有 \(B\) 元钱,最多买多少个物品?
\(n\le 5000,x_i<i\)。
标签:树形 dp。
显然购买限制条件构成一棵树,如果一个物品使用优惠券就必须让根节点到它路径上的点都被买。
设 \(f_{i,j,0/1}\) 表示以 \(i\) 为根的子树中选了 \(j\) 个物品,是否使用优惠券的最小价格。
树上背包暴力转移 \(O(n^3)\),有个经典结论是可以枚举到子树大小,时间复杂度 \(O(n^2)\)。
CF1428F *2400 \(\color{blue}\bigstar\)
给定一个 01 串,设 \(f(l,r)\) 为从 \(l\) 到 \(r\) 的子串中,最长的全部为 \(1\) 的子串的长度。
求 \(\sum_{l=1}^n\sum_{r=l}^n f(l,r)\)
\(n\le 5\times 10^5\)。
码量最短的 *2400。
考虑把原式变换 \(g_i\) 表示含有长度为 \(i\) 的区间数量。
可以发现
原因可以考虑每个长度的串对答案的贡献。
考虑咋求 \(g_i\)。
考虑把长度 \(\ge i\) 的子串拿出来:

红色的是拿出来的。
从后向前考虑,分两种情况。
- 在某个子串的最后。

那么对答案的贡献就是两个绿色部分之和,因为前面的已经被计算过了。
- 在某个子串前面。
对答案的贡献就是 \(i\),因为后面多了一个右端点。
然后咋做呢?
可以发现如果是第二种情况可以所有长度的贡献都是 \(i\),所以只需要考虑第一种情况。
记录一下向后最长的长度 \(s\),记录一下该长度做第一种情况时的右端点 \(las_s\)。
直接边做边更新就好了。
CF379F *2400 \(\color{gray}\bigstar\)
有一颗 \(4\) 个节点的树,\(2,3,4\) 号节点的父亲节点都是 \(1\)。\(m\) 次操作。操作有 \(1\) 种:
u:设现在这颗树有 \(n\) 个节点,则您要新建两个节点 \(n+1,n+2\) 并让它们变为 \(u\) 的儿子节点(连一条 \(u\) 到 \(n+1\) 的边和 \(u\) 到 \(n+2\) 的边)。保证 \(u\) 是叶子节点。进行完操作后,您要输出此时树的直径。
标签:树论。
有一个很典的直径结论,两棵树合并查子树只需要拿出两棵树各自的直径,一共 \(4\) 个点找最长即可。
这题也是,直接看看新增的两个点是否可以更新直径就好了。
CF632E *2400 \(\color{Gold}\bigstar\)
已知 \(n\) 个物品,第 \(i\) 个物品价值为 \(a_i\),可以拿恰好 \(k\) 个物品,输出所有可能拿到的价值和。
\(n,a_i,k\le 1000\),时限 \(5s\)。
标签:生成函数,多项式,背包。
看到标签中的 fft,先想生成函数。
其实比较好构造。
就相当于每次选一个,选 \(k\) 次。
答案就是系数不为零的项的指数。
暴力做复杂度 \(O(kn^2\log (n^2) )\),爆炸,分治 NTT 做,时间复杂度 \(O(n^2\log (n^2))\),可过。
结果发现这题直接背包就好了。。。
考虑如果不是恰好,而是不多于,那么直接设 \(f_i\) 表示要选出 \(i\) 价值最少需要拿多少物品,判断 \(f_i\le k\) 即可。
考虑如果有一个物品价值是 \(0\) ,那么就是不多于了,因为多出来的空位可以用 \(0\) 补。
由于总共拿 \(k\) 个物品已知,所以所有物品的价值减去一个最小值,这样就有了一个价值为 \(0\) 的物品,然后就没了。
时间复杂度 \(O(n^3)\),常数比较小,可以过。
CF1523D *2400 \(\color{Gold}\bigstar\)
有 \(m\) 种货币 \(n\) 个商人,已知第 \(i\) 个人是否喜欢第 \(j\) 种货币且每个人至多喜欢 \(p\) 种货币。选择最多个货币种类使得有不少于 \(\lceil \frac{n}{2}\rceil\) 个人喜欢所有选出的货币种类。
\(n\le 2\times 10^5,p\le 15,m\le 60\)。
标签:随机,FWT。
考虑暴力咋做,对于每个数枚举其子集,然后看看是否有满足条件的。
时间复杂度 \(O(n2^p)\),爆炸。
然后就有一个很牛的随机化算法,因为需要 \(\frac{n}{2}\) 个人满足条件,所以随机一个人,让他一定满足条件,这样概率挺大。
随机之后,直接对所有数做一遍后跑一遍 FWT,知道每个子集出现的次数就行了。
时间复杂度 \(O(T(n+2^p))\)。
出数据的人很友好,如果你 srand(time(0)) 然后直接拿出 rand()%n+1 会 WA,需要 rand()*rand()%n+1。
CF786C *2400 \(\color{blue}\bigstar\)
将 \(n\) 个数划分成 \(m\) 段使得每中不同数字的个数 \(\le k\). 对于每个 \(k\) 满足 \(1\le k\le n\) 求出最小的 \(m\)。
标签:根号分治。
如果已知一个 \(k\),显然可以直接求 \(m\),暴力时间复杂度 \(O(n^2)\)。
显然答案单调不增。
观察样例可以发现后面的数都趋于稳定了,考虑根号分治。
如果 \(k\ge \sqrt{n}\),那么对应的 \(m\le \frac{n}{k}\),即 \(m\le \sqrt{n}\),小的暴力,大的二分一下答案相同的区间就做完了。
时间复杂度 \(O(n\sqrt{n}\log n)\),时限 \(2s\),稍微卡常一下可过。
调整块长为 \(\sqrt{n\log n}\) 后复杂度平衡为 \(O(n\sqrt{n\log n})\),跑得飞快,\(1s\) 以内就通过了。
好像有 \(O(n\log^2 n)\) 的做法?
CF1096G *2400 \(\color{green}\bigstar\)
一个 \(n\) 位数,每位可以是给出的 \(k\) 个数码中的一个数,可以有前导 \(0\),输出前 \(\frac{n}{2}\) 位之和与后 \(\frac{n}{2}\) 位之和相等的方案数,保证 \(n\) 是偶数,答案对 \(998244353\) 取模。
\(n\le 2\times 10^5,k\le 10\),时限 \(5s\)。
标签:生成函数,分治NTT。
看到总数一定和 \(998244353\),一眼生成函数。
考虑对于一个和,直接算出方案数的平方加起来。
直接求它的 \(n/2\) 次方就好了。
时间复杂度 \(O(nk\log nk)\)。
code。
神鱼有个很神的 \(O(nk^2)\) 做法,可惜我不大会。
CF220E *2400 \(\color{gray}\bigstar\)
给你一个长度为 \(n\) 的序列 \(A_1, A_2, …, A_n\). 问你有多少组 \((l, r),l<r\) 满足 \(A_1, A_2, …, A_l, A_r, A_{r+1}, ..., A_n\) 的逆序对个数不超过 \(k\)。
标签:树状数组,双指针。
显然区间越大越容易满足条件,对于一个左端点找到最小的右端点即可。
双指针扫一遍,没了。
CF915F *2400 \(\color{green}\bigstar\)
给定一棵树,每个顶点都被写上了一个数,第 \(i\) 个顶点写上的数是 \(a_i\)。定义一个函数 \(I(x,y)\) 表示从顶点x到y的简单路径上 \(a_i\) 的最大值和最小值的差。
求\(\sum_{i=1}^{n}\sum_{j=i}^{n}I(i,j)\)
标签:并查集。
拆成最大值和最小值两个询问,然后考虑每个点对答案的贡献,以最大值为例,那么就是把点权小于等于自己的点集拿出后算经过这个点的路径数,这个可以直接并查集动态维护,然后统计一下答案就做完了。
code。
CF5E *2400 \(\color{blue}\bigstar\)
一个圆环上依次有 \(n\) 个塔,每个塔上站着一个人,如果两个塔中间的塔都不超过这两个塔的高度,那么两个人就可以相互看到(可以顺时针和逆时针两种方向),问有多少对塔可以相互看到。
标签:树状数组。
题解都是单调栈,可惜我太菜了不会。
考虑计算每个塔对答案的贡献,一个塔对我们在较矮的塔哪里统计答案。
考虑如果高度是一个排列,那么答案显然就是 \(2n-3\),因为最高的塔不会产生贡献,第二的只能看到最高的,下面的都只能看到左右第一个比自己高的塔,所以答案是 \(2n-3\)。
考虑有相同高度的情况,那么显然找到左右第一个比自己高的塔后,这段区间中所有和自己高度相同的塔都是可以看到的,全部加起来后除以二就好了,可以直接用 set 查询这段区间的左端点和右端点,然后树状数组查询区间和。
时间复杂度 \(O(n\log n)\),常数有点大,跑进了洛谷最优解的最后一页。
我是 sb,其实 \(O(n)\) 做法很简单。
先破环成链,依然是找左边和右边第一个比自己大的。
以左边为例,如果左边的比自己大,那么就找到了。
否则就跳到左边的区间左端点,继续向左跳就好了。
AGC002D *2514 \(\color{green}\bigstar\)
一张连通图,\(Q\) 次询问从两个点 \(x\) 和 \(y\) 出发,经过的点集之和大小为 \(z\),经过的边最大编号最小是多少。
\(n\le 10^5,Q\le 10^5\)
每次询问显然可以二分答案然后并查集维护联通快大小来判断。
显然整体二分,需要用可持久化并查集维护,时间复杂度 \(O(n\log^2 n)\)。
还有一个 Kruskal 重构树做法,这里口胡一下。
就考虑其实只需要留下最小生成树上的边,其他边都可以删去,那么重构树上一棵子树的大小就是一个联通块的大小。
二分答案一下,倍增向上跳,看看子树大小是否满足条件即可。
时间复杂度也是 \(O(n\log^2 n)\)。
CF449C *2500 \(\color{blue}\bigstar\)
给出正整数 \(n\),你要把 \(1-n\) 之间的正整数分成尽可能多组,使得每一组两个数的最大公约数大于1;输出方案。
标签:构造,贪心。
猜结论好题。
显然考虑每个质因数,把它们的倍数拿出来,如果有偶数个显然直接匹配,如果奇数就要去掉一个。
但会出现 \(6\) 这样的数,即在 \(2\) 的倍数中,又在 \(3\) 的倍数中,很难考虑。
一个显而易见的做法是从大到小做,因为一个数是小质因数倍数的概率更加大,如果从小到大考虑,去掉那个数就很难考虑。
从大到小,如果是偶数就直接匹配,如果是奇数就随便把一个 \(2\) 的倍数去掉后匹配。
容易发现这样的贪心策略显然最优。
[AHOI2012]树屋阶梯 \(\color{CornflowerBlue} {提高+/省选-}\) \(\color{green}\bigstar\)
已知一个高为 \(n\) ,第 \(i\) 层长度为 \(i\) 的阶梯,每次可以选择覆盖其中一个没有被覆盖的矩形,需要用 \(n\) 次全部覆盖,求方案数。
标签:卡特兰数。
既然要 \(n\) 次覆盖,考虑左下角是 \((0,0)\) 的矩形,它的右上角一定是边界,所以就把问题分成了两个部分。
显然卡特兰数,直接用这个求。
凉心出题人没有模数,所以写高精。
CF1342E *2300 \(\color{Gold}\bigstar\)
有这样一个问题:
在 \(n \times n\) 的国际象棋棋盘上放 \(n\) 个车,要求满足两个条件:
所有的空格子都能被至少一个车攻击到。
恰好有 \(k\) 对车可以互相攻击到。
答案对 \(998244353\) 取模。
标签:组合数学,容斥。
首先一个比较显然的结论,每个空格子都要被攻击到,那么要么每行都要有一个棋子,要么每列都要有一个棋子,证明比较显然。
所以只需要考虑行的,然后答案去乘 \(2\) 就好了。
可以发现,如果 \(n\) 个棋子放在 \(n\) 行 \(m\) 列,每行至少有一个棋子,每列至少有一个棋子,那么互相攻击的对数是 \(n-m\)。
所以就相当于把 \(n\) 个棋子放在 \(n\) 行 \(n-k\) 列中。
类似于第二类斯特林数,直接容斥就好了。
注意特判 \(k=0\) 的情况,此时不需要乘 \(2\)。
CF1425D *2300 \(\color{blue}\bigstar\)
有一个 \(1000\times 1000\) 的地图,有 \(n\) 条蛇,第 \(i\) 条蛇在 \((x_i,y_i)\),攻击值为 \(w_i\),每条蛇的攻击集合为与自己切比雪夫距离 \(\le r\) 的蛇(自己也算)。
现在选择其中 \(m\) 条蛇,将这些蛇的攻击集合取并集,则这种选择方案对答案的贡献就是该集合中所有蛇的和的平方,求所有选择方案的答案是多少。
\(n\le 2\times 10^3\),答案对 \(10^9+7\) 取模。
标签:组合数学,容斥。
考虑选出的集合是 \((a_1,a_2,a_3...a_k)\),那么对答案的贡献是:
考虑左右各选一个数对答案的贡献。
如果集合中要同时又这两个数,有两种情况:
-
有一条蛇的攻击集合包含这两条蛇。
-
有两条蛇的攻击集合分别包含着着两条蛇。
先算上面的,假设满足这个条件的蛇有 \(s_1\),条,其中至少选一条,容斥一下答案就是
考虑第二种情况,假设能包含第一条蛇的有 \(s_1+s_2\) 条,能包含第二条蛇的有 \(s_1+s_3\) 条,容斥一下可以得到:
查询 \(s_1,s_2,s_3\) 可以用二维前缀和。
两者相加,算一下贡献,做完了。
\(37\) problems now。


