摄像机模型

作者：@houkai
本文为作者原创，转载请注明出处：https://www.cnblogs.com/houkai/p/6363135.html

---

摄像机是三维空间物体与二维图像之间的一种映射。成像模型就是三维空间物体到二维视平面的投影关系。

针孔模型

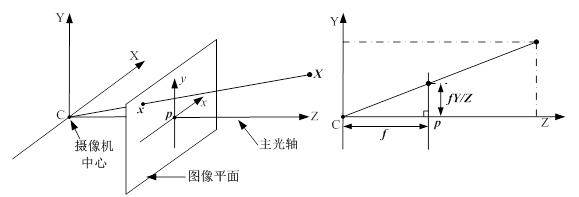
透视投影（Perspective Projection）是最常用的成像模型，可以用针孔成像模型来近似表示。透视投影成像模型的特点是所有来自场景的光线均通过一个投影中心，它对应于透镜的中心，经过投影中心且垂直于图像平面（成像平面）的直线称为投影轴或光轴。

中心投影可以非常简单地表示成齐次坐标之间的线性映射。

为摄像机坐标系中的物体坐标 是物体投影在图像平面的位置。

则有 , 其中K为3*4的摄像机投影矩阵。

摄像机模型

针孔模型的X是相对摄像机坐标系而言的，而往往摄像机是不断运动的（位姿在不断变化），空间点的世界坐标系是恒定不变的。摄像机坐标系和世界坐标系可以通过旋转和平移相联系。

R是摄像机相对于世界坐标系的旋转矩阵，C表示位移。令 得:

摄像机模型可表示为：

此处X是世界坐标系下的位置。

上述推导的摄像机模型是假定图像坐标在两个轴向上有等尺度的欧式坐标。但CCD摄像机的像素可能不是正方形。如果图像坐标以像素来测量，那么需要在每个方向上引入非等量尺度因子。

所以：

其中 、 ,m分别表示在x和y方向上图像坐标单位距离的像素数, 表示像素量纲上图像的原点。

摄像机模型的参数

K是内参，R和t成为外参。

R为旋转矩阵

在三维空间中，旋转可以分解为绕各自坐标轴的二维旋转，如果依次绕x,y,x轴旋转角度

旋转矩阵R可以表示为 , , 的乘机，因此 

t为平移向量

表示摄像机坐标系原点在世界坐标系中的位置。

内外参数

P有10个自由度，3个来自R，3个来自t，4个是K中的内参。另外，由于P为3*4的不可逆矩阵，在已知P的情况下，为了得到空间点的三维世界坐标，就必须有两个或更多的相机构成的视觉系统模型才能实现。