5.7 除法器的优化
计算机组成
5 乘法器和除法器
5.7 除法器的优化

我们现在的这个除法器已经可以正常的工作了。但是距离实用还有相当大的距离,必须要经过优化,不过除法的优化就比较复杂。因此,在这一节,我们只是对它的优化方法和优化的方向做一个非常基本的探讨。
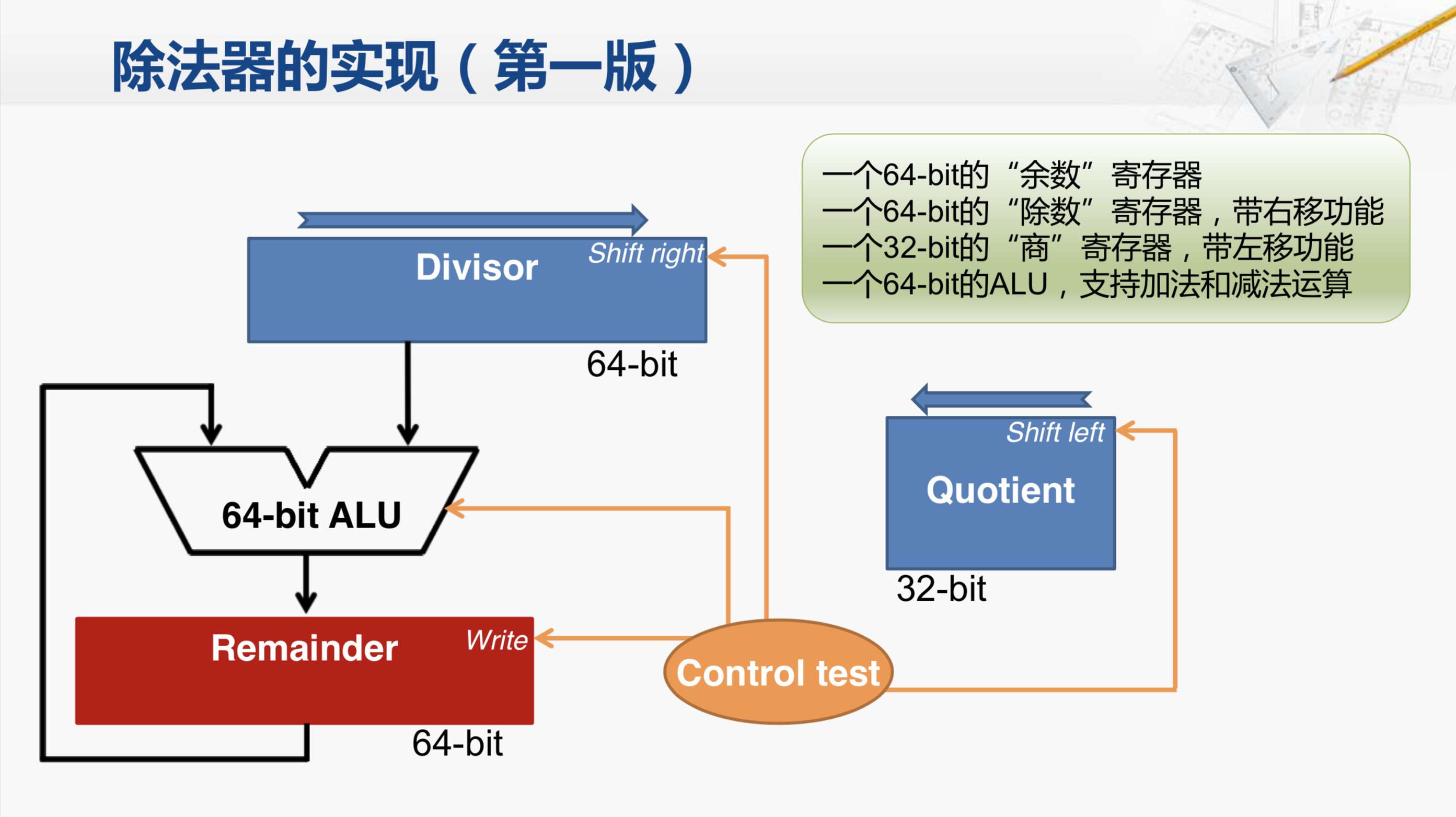
这是我们已经有了的这一版除法器,我们不妨称之为第一版的实现。在这个除法器当中,有一个64位的余数寄存器;一个64位的除数寄存器;一个32位的商寄存器和一个64位的ALU。
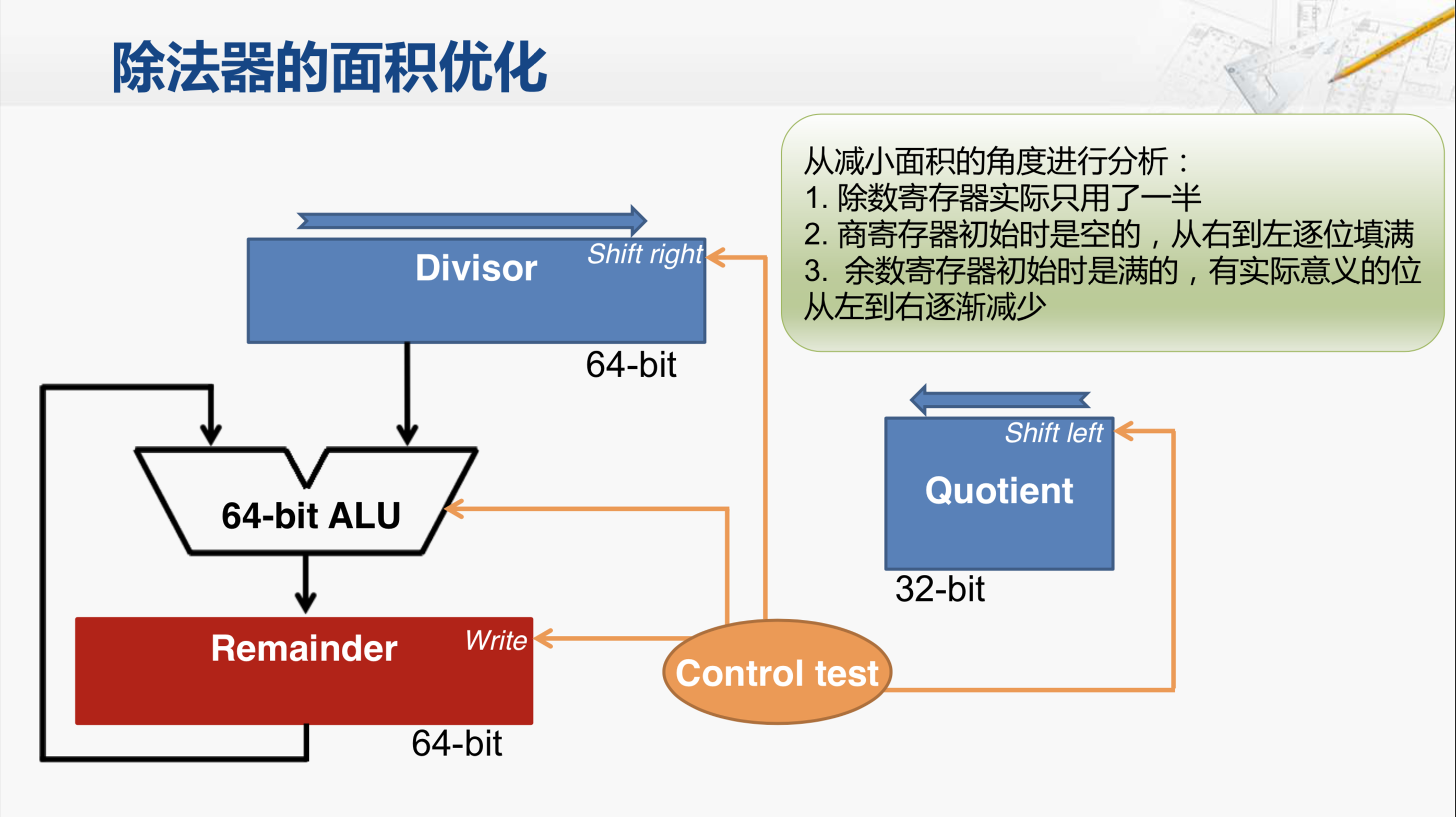
那我们首先来考虑面积方面的优化,我们先来看看在哪些地方存在着浪费。
首先,我们的除数是只有32位的,而我们的除数寄存器使用了64位的,实际只使用了其中的一半,这是第一个可以优化的点。
第二,商寄存器在初始化的时候是空的,每执行完一轮会产生移位,从右向左逐位填满。所以,这里也存在着浪费的情况。
第三,余数寄存器初始时是满的,也就是最开始的被除数。但是,在不断进行和除数的减法之后这个余数会变得越来越小,它有实际意义的位从左往右在逐渐地减少。所以,越往后,余数寄存器当中浪费的位就会越多。
那我们就尝试从这三个方面进行面积上的优化。
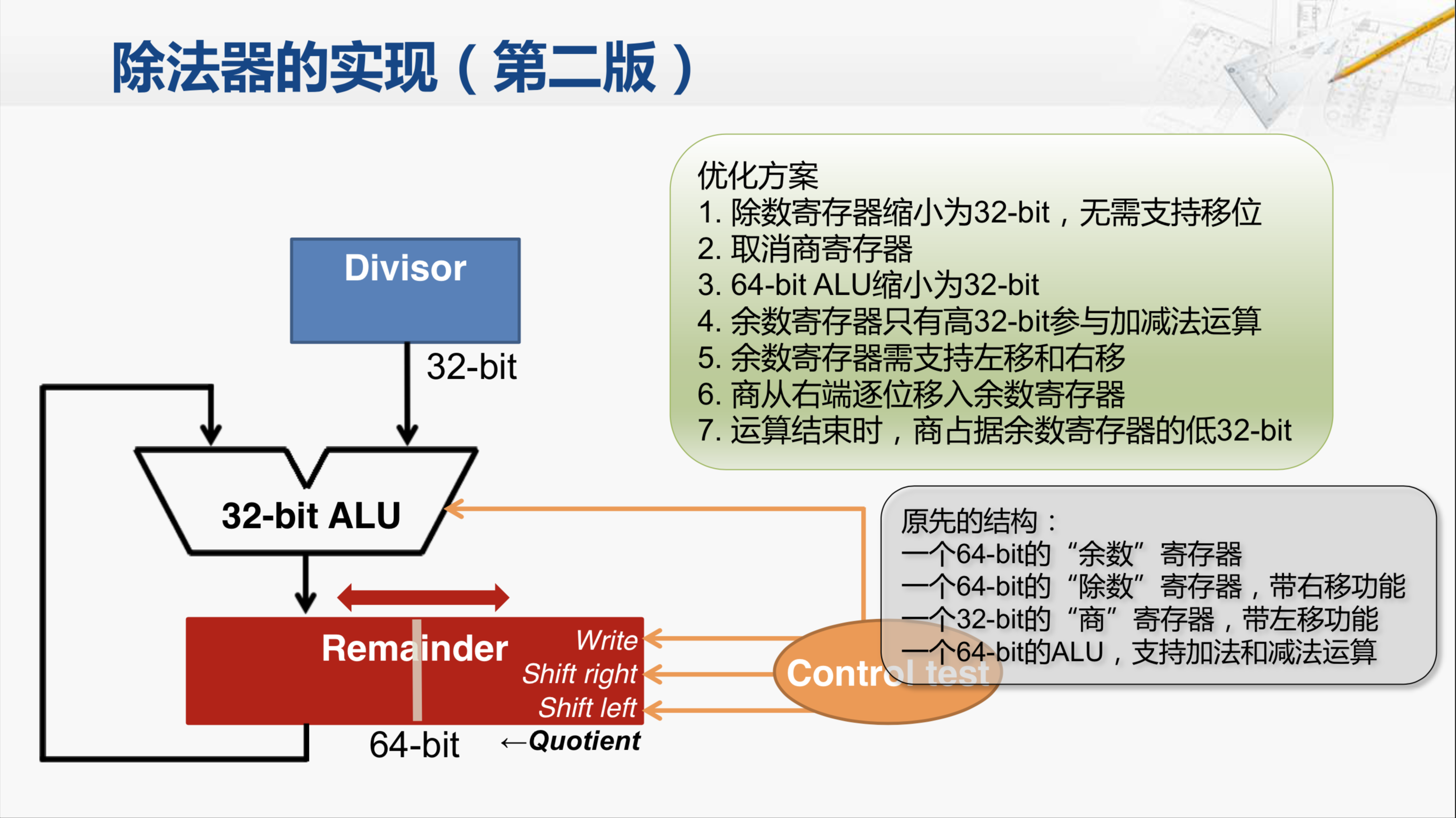
那我们把经过面积优化的除法器称为第二版,我们就来看一看第二版的除法器是什么样的。为了方便对比,我们把优化方案和原来结构的描述放在一起。
首先,原先有一个64位的除数寄存器,现在我们将除数寄存器缩小为32位,因为除数本来就是32位的,所以这样除数寄存器就没有了浪费的情况。但是我们要注意,除数寄存器是在整个运算过程中一直要使用的,它的移位只是为了和余数寄存器进行对齐,以方便运算。所以,原先才准备了一个64位的寄存器,以便于除数在移位的过程中也不会丢失。那现在将它缩小为32位了,就不能再有移位的功能,否则其中有效位就会丢失了。因此,这个除数寄存器也就不用再支持移位功能。那么在运算中需要将除数和余数进行对齐的这项功能,就得放到别的地方来完成了。
第二,我们知道原来有一个32位的商寄存器,它一开始是空的,在运算的过程中逐位填满。那既然它一开始没有用,所以我们干脆先取消这个寄存器,再看一看可不可以在别的地方实现类似的功能。
第三,原来有一个64位的ALU。而我们知道,实际参与运算的其中一个操作数是除数,另一个操作数则是余数寄存器当中和除数对应的一些位,实际上只有32位。所以,我们就将这个64位的ALU缩小为32位,也就是说只要让其中有效位数参与运算。
那么对于余数寄存器,或者说一开始是被除数的这个寄存器,它在和除数进行减法运算时,最开始只有最高的32位参与运算,之后才逐次地往低位移动。所以,我们先规定这个余数寄存器只有高32位参与这个加减法运算,我们也在这个余数寄存器当中画一条半透明的线作为标记,而整个余数寄存器仍然保留为64位,其中的高32位被连接到ALU的一个输入,而ALU的输出也连接到了余数寄存器的高32位。
但是,原来除数寄存器是带有右移的功能,从而实现了余数寄存器中参与运算的数逐渐向低位移动这样一个情况,那现在除数寄存器已经不能右移了。与之相对,余数寄存器那就得支持一个左移的功能,而且我们再去回顾除法的运算过程可以发现,余数或者说被除数的高位一旦退出了运算,就不再会有机会重新参与运算了。所以,把余数寄存器的高位向左移位,并将移出的位丢弃,是不会对运算的过程造成影响的。所以,我们将余数寄存器加上左移的功能。而实际上我们发现,现在这个余数寄存器不仅支持左移,还支持右移的功能。为什么支持左移?刚才我已经介绍了;而为什么支持右移呢?就留给大家自己来思考。
当然,什么时候进行移位需要由控制逻辑进行控制。所以,在余数寄存器上也需要有相应的控制输入。那现在我们要注意的是,余数寄存器的浪费问题仍然没有解决。随着运算的进行,每一轮余数寄存器都会向左移位一次,它的右边则会多空出一位来,而且空出的位会越来越多。那么我们回头来看一看,其中我们还需要一个32位的商寄存器,而且这个商在运算的一开始是不需要占据任何空间的,只需要每一轮采用左移的方式,给它多分配一个比特就可以了。那就正好是余数寄存器现在所浪费的情况,我们就可以很自然地将商寄存器合并到余数寄存器当中。让每一轮产生的商,从余数寄存器的右端逐个移入。这样当运算结束时,商就占据了余数寄存器的低32位,而余数寄存器的高32位,则是最后真正的余数。这样再连上对应的控制逻辑之后,我们就有了一个经过面积优化的除法器。
那么在实现了面积优化之后,我们就要考虑在性能上是否可以进行优化。
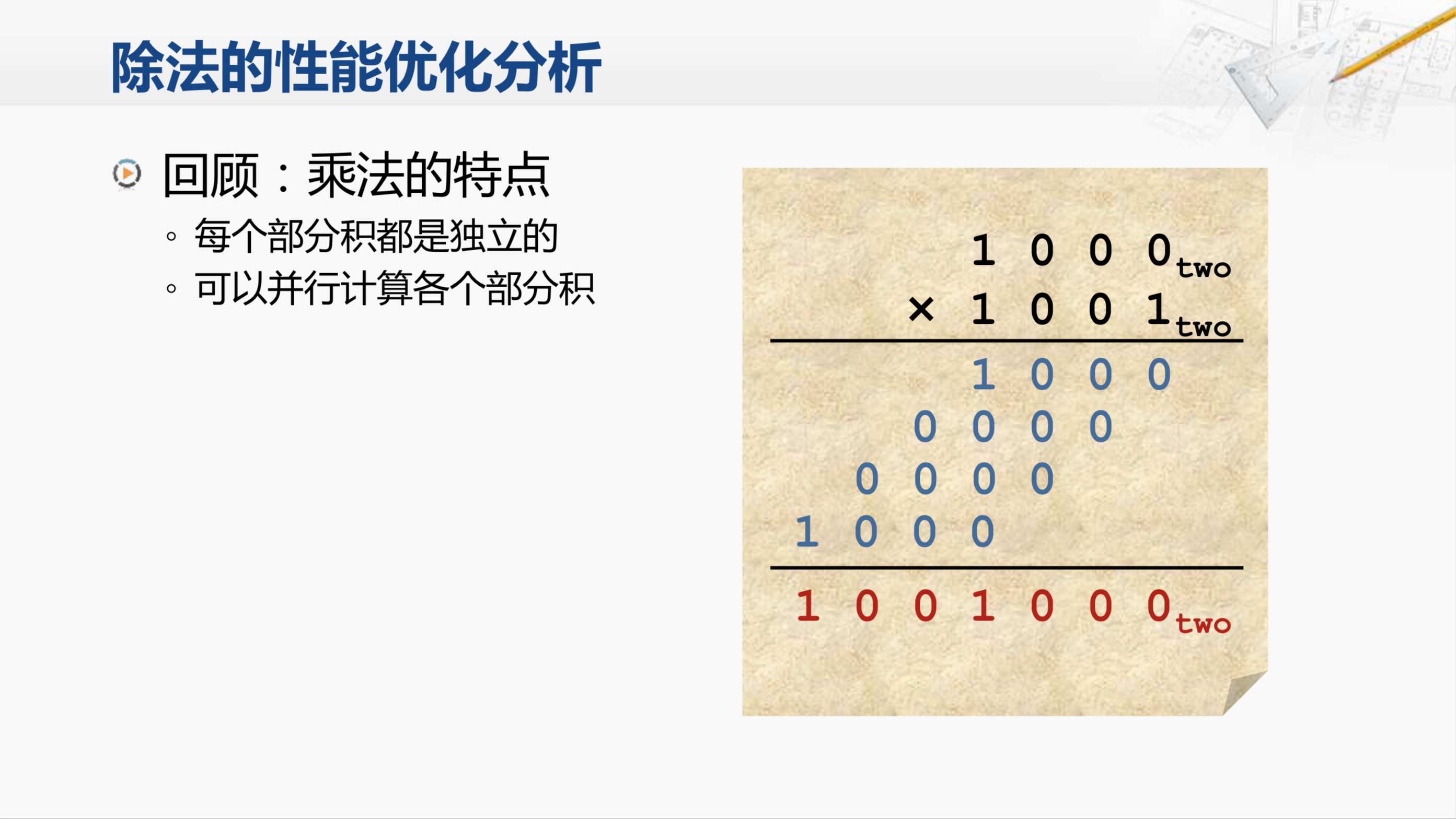
想进行除法器的性能优化,我们就要先来回顾乘法是如何进行优化的。其实现在的乘法器可以做到非常好的优化,这和乘法运算自身的特点是分不开的。
我们来看之前提到过的例子,仔细分析就可以发现,虽然乘法和除法都要产生很多中间的结果,也都需要通过移位等操作进行对齐,再进行最后的运算。但是很大的不同在于,乘法的每一个中间结果都是独立的,每一个中间结果,要么和被乘数相等,要么是0,而且它究竟是哪一种?只由乘数当中固定的一位决定,不受其它位的影响。所以,如果我们人工进行乘法的计算,当我们有了被乘数和乘数之后,可以交给很多人来协作运算。每个人只计算其中一个中间结果,然后再由一些人将这些中间结果加起来,这样就可以通过并行的计算大幅度地提高性能。
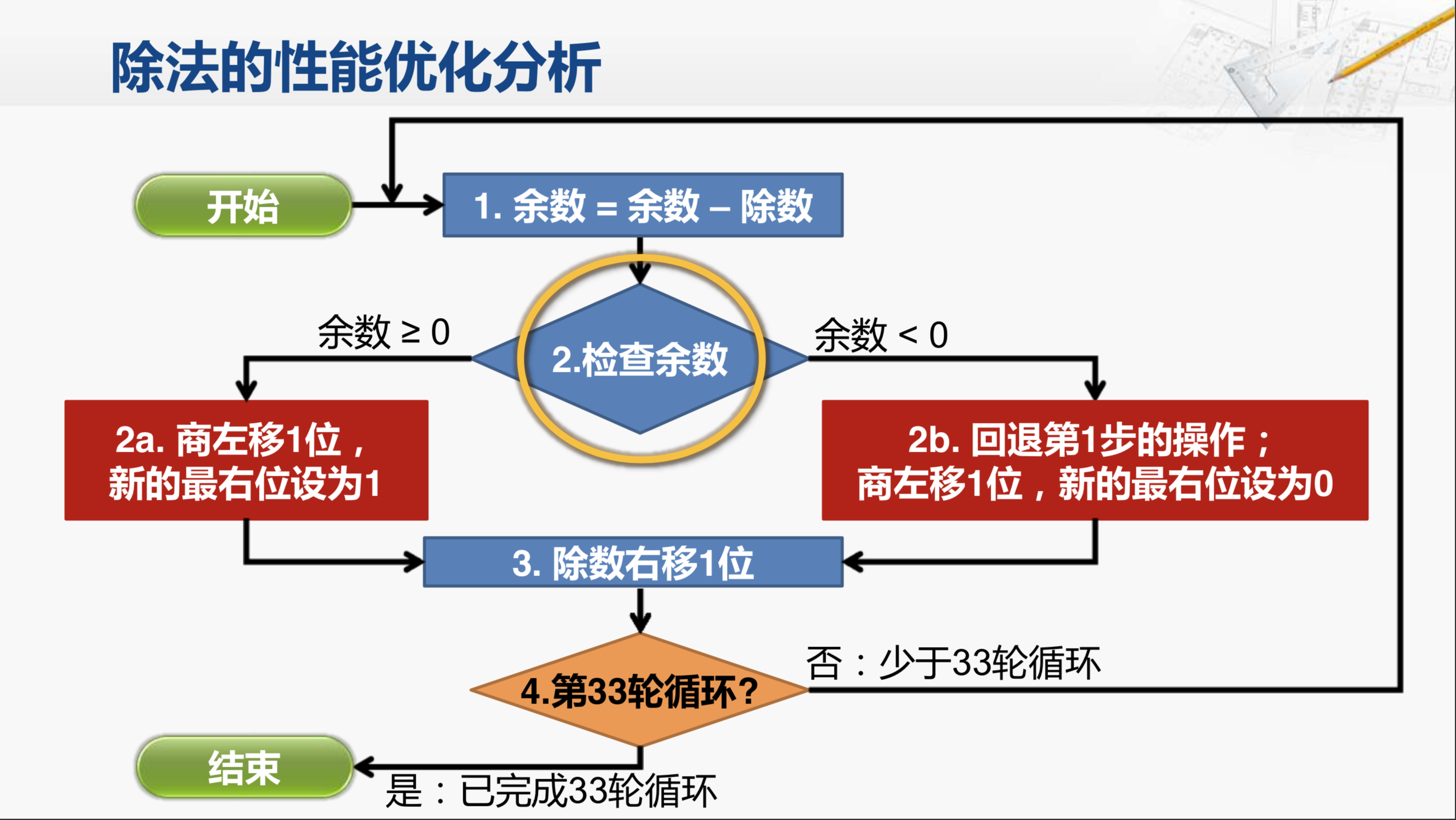
而我们来看除法的这个工作流程,中间有一个检查余数的工作,而且当余数小于0时,还需要回退第一步的操作。这实际上就是因为除法的这些中间结果并不是各个独立的。那我们可能会想到,乘法的那个流程图当中,不也有一个要进行检查的分支操作吗?看上去和除法这个流程图是非常相似的。那么,不妨把乘法的这个流程图找出来仔细地看一看。
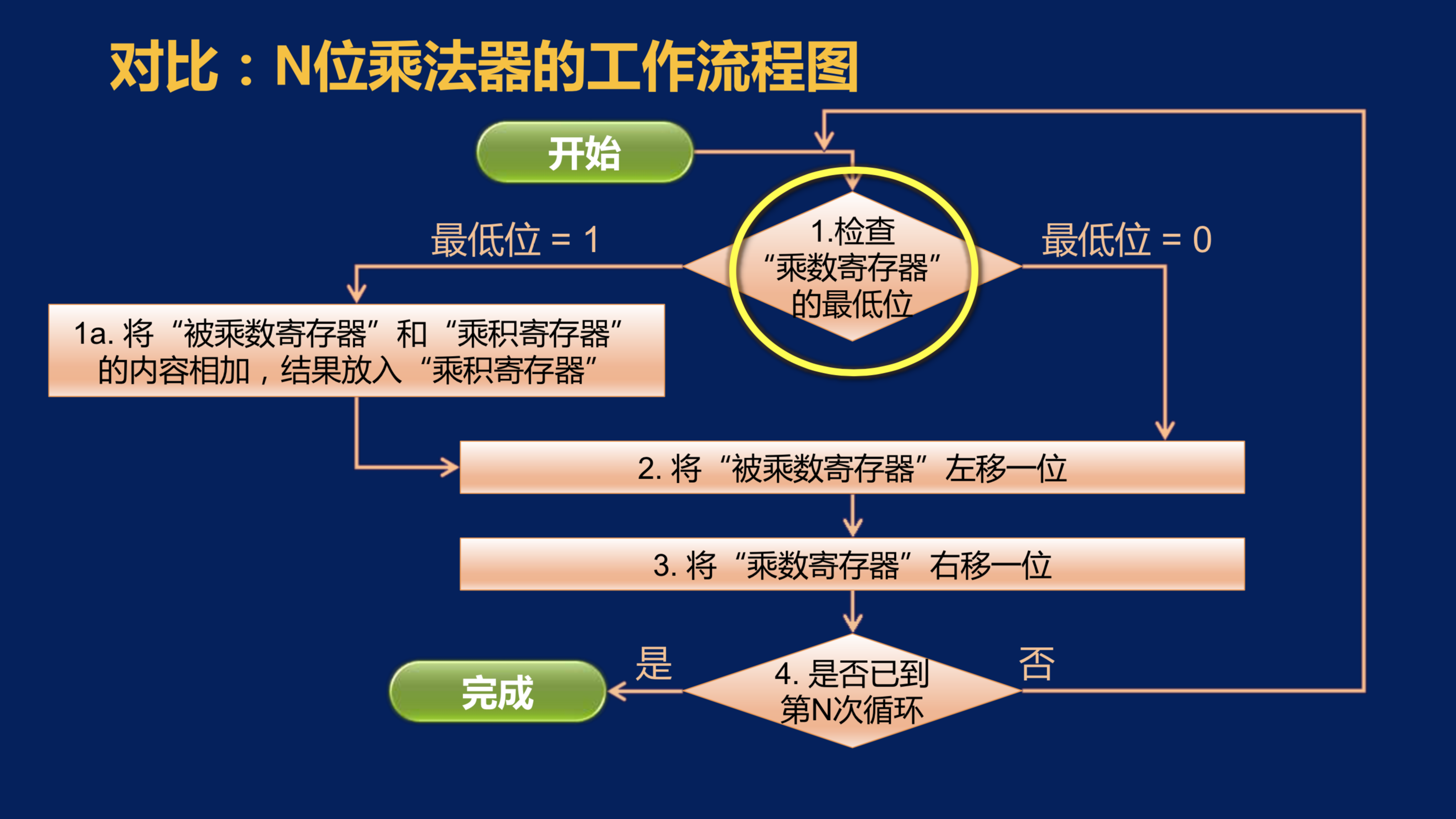
的确。在开始的这个地方确实有一个检查乘数寄存器的最低位的操作,并且根据检查结果的不同会走向两个不同的分支。但是,我们仔细分析就会发现,这个分支实际上是不存在的。因为当最低位为1时,会执行将被乘数寄存器和乘积寄存器相加,这样一个操作。那么我们不妨可以理解为,将被乘数寄存器的内容和乘数寄存器的最低位进行一个”与操作“,然后再和乘积寄存器相加,因为现在乘数寄存器的最低位是1,任何数和1进行”与操作“,结果还是这个数本身,所以,这样的改动并不会影响这里的操作;而对于这一边,当最低位为0时,如果我们也做同样的操作,也就是将乘数寄存器的最低位和被乘数寄存器先进行”与操作“,然后再和乘积寄存器相加,因为任何数和0进行”与操作“,结果都是0,0再和乘积寄存器相加,那就相当于没有执行加法操作,乘积寄存器的内容并没有改变。所以,实际上我们可以将这个分支取消,在每轮的最开始都直接将乘数寄存器的最低位和被乘数寄存器进行”与操作”,然后和乘积寄存器相加。这样无论最低位是1,还是0,都能完成这个工作流程图所表达的工作。
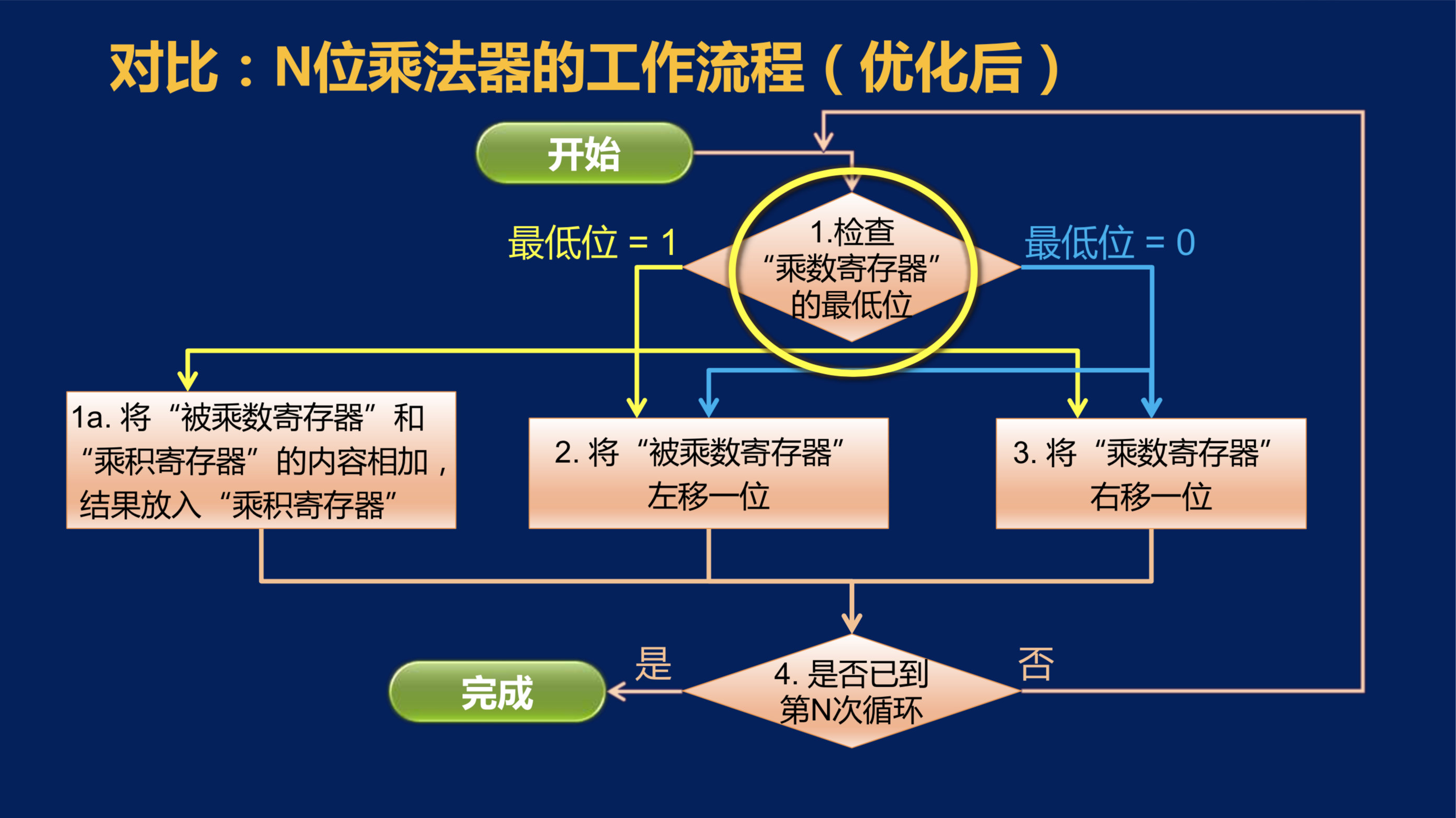
那即使对于这个优化后的工作流程,效果也是一样的。因为第一步的检查之后,2和3这两步操作都会执行,唯一的区别在于1a这个操作。所以,采用刚才所描述的那种修改(前一个图片提供的修改方案,引入“与操作”),也可以达到同样的效果。因此,对于这个工作流程来说,在实际的实现当中也可以不存在这个分支的操作。
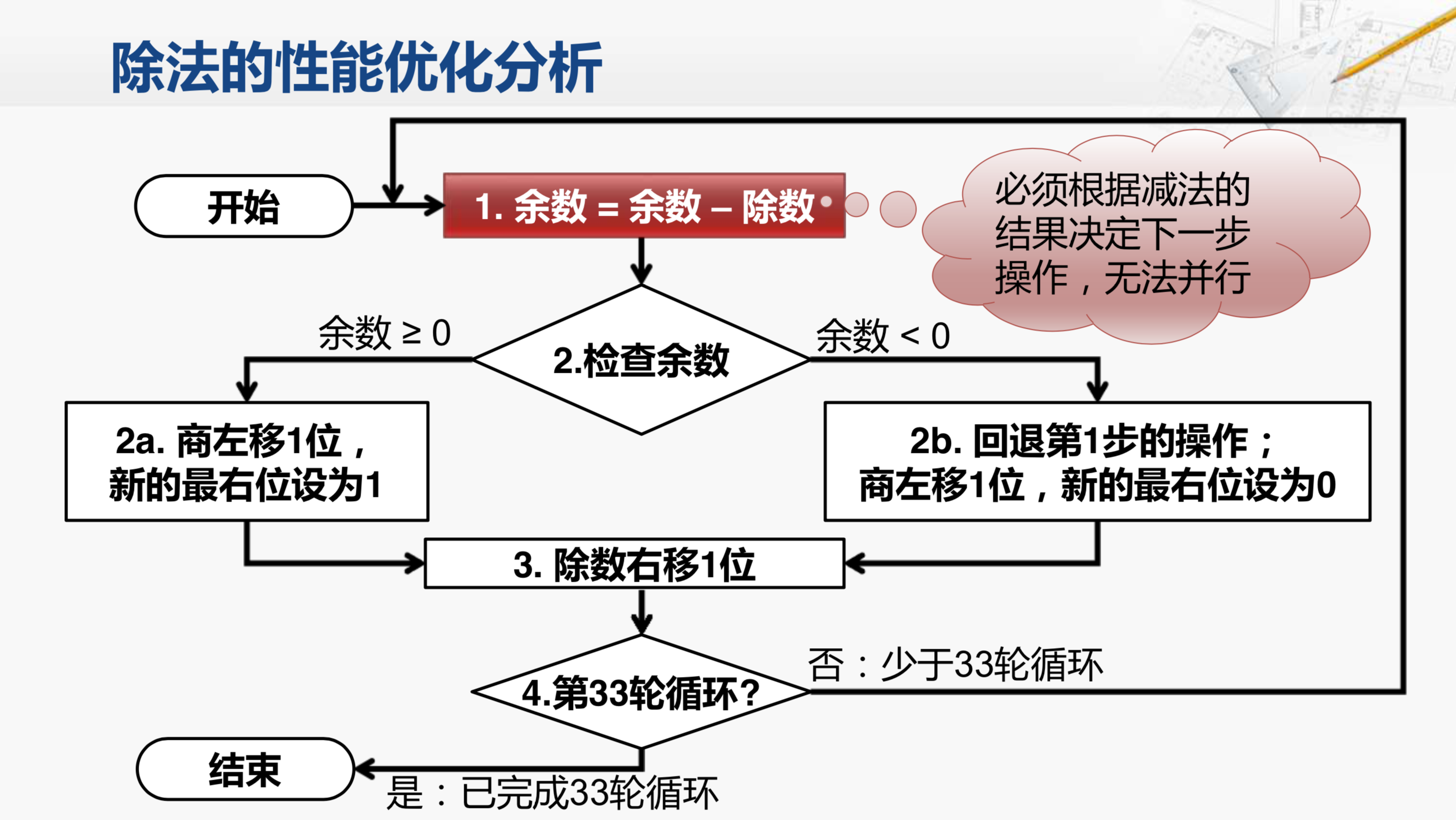
然而对于除法的这个工作流程,这一次减法的运算结果是事先无法预知的。因此,无法预知下一步将执行哪一个分支,而且其中一种分支还需要将这个减法操作进行回退。所以,也没有办法将两个分支进行合并。因此,在这个除法运算流程的大框架之下,是很难进行进一步的性能优化了。

正是由于除法的优化非常的困难,因而也引来了很多人对除法进行深入的研究,也产生了很多很有趣的,快速除法的实现方法。如果你对此有兴趣,可以进一步深入地探索。

