4.6 加法器的优化

计算机组成

4 算术逻辑单元

4.6 加法器的优化

ALU提供的加法和减法，究其本质都是由加法器来实现的。我们现在学习的加法器，是由一个一个的全加器串联而成，它在性能上存在着很大的问题，而这个问题究竟是什么？我们又该如何解决？在这一节，我们将来一起探讨这件事情。

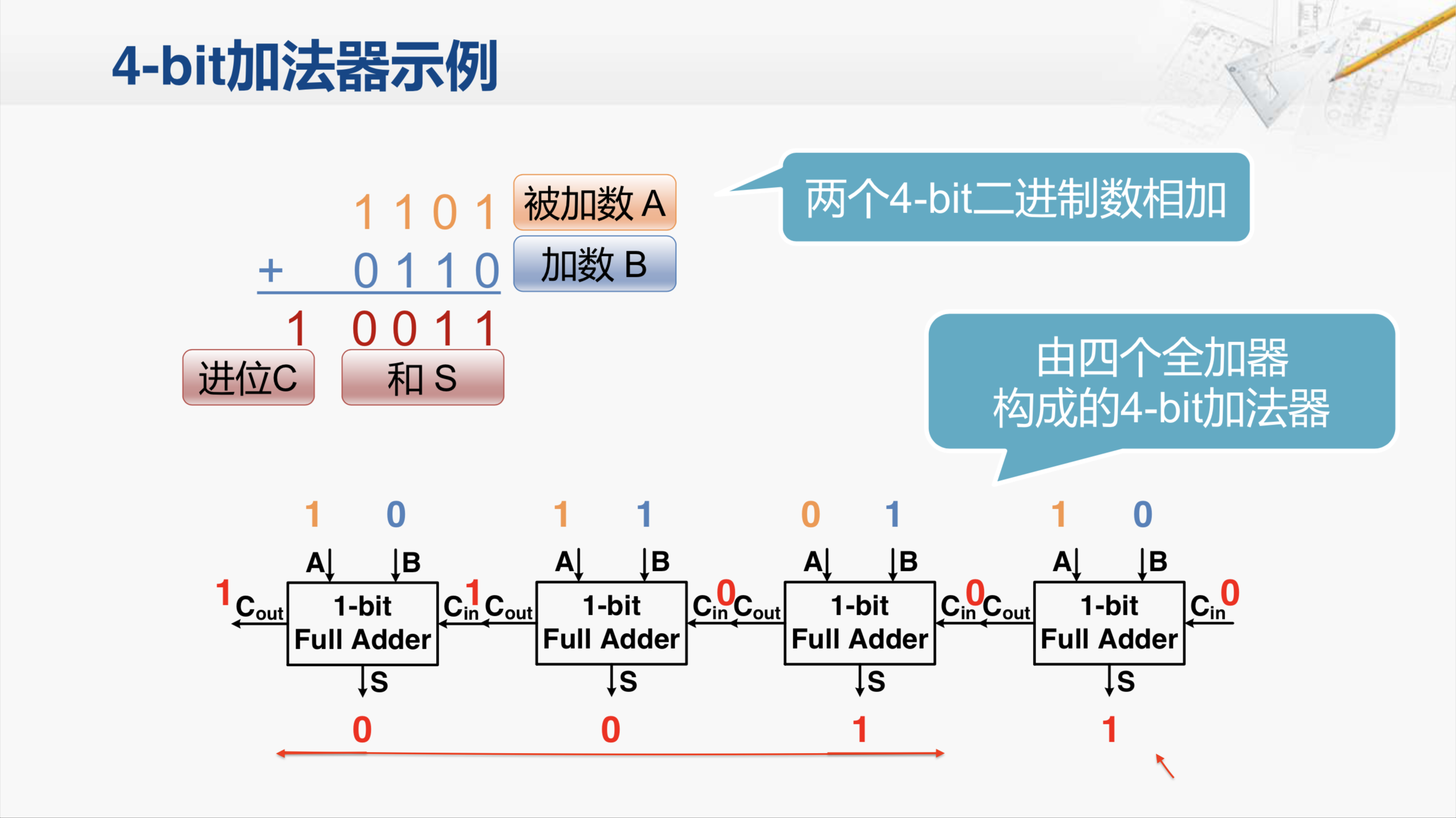
我们还是来看这个四位加法器的例子，在实现中我们是用四个全加器构成了这个四位的加法器。我们注意到，当把这个加法器的输入都准备好时，其实只有最右边的这个全加器的三个输入都准备好了；左边这三个全加器，它的进位输入Cin都还没有产生。所以实际上只有最右边这个全加器可以得到正确运算结果，等它将进位的输出Cout传递到下一个全加器后，下一个全加器才可以开始运算，进而产生新的进位输出。这样进位输出像波浪一样，依次从低位到高位传递。这样的加法器也因此得名为行波进位加法器。

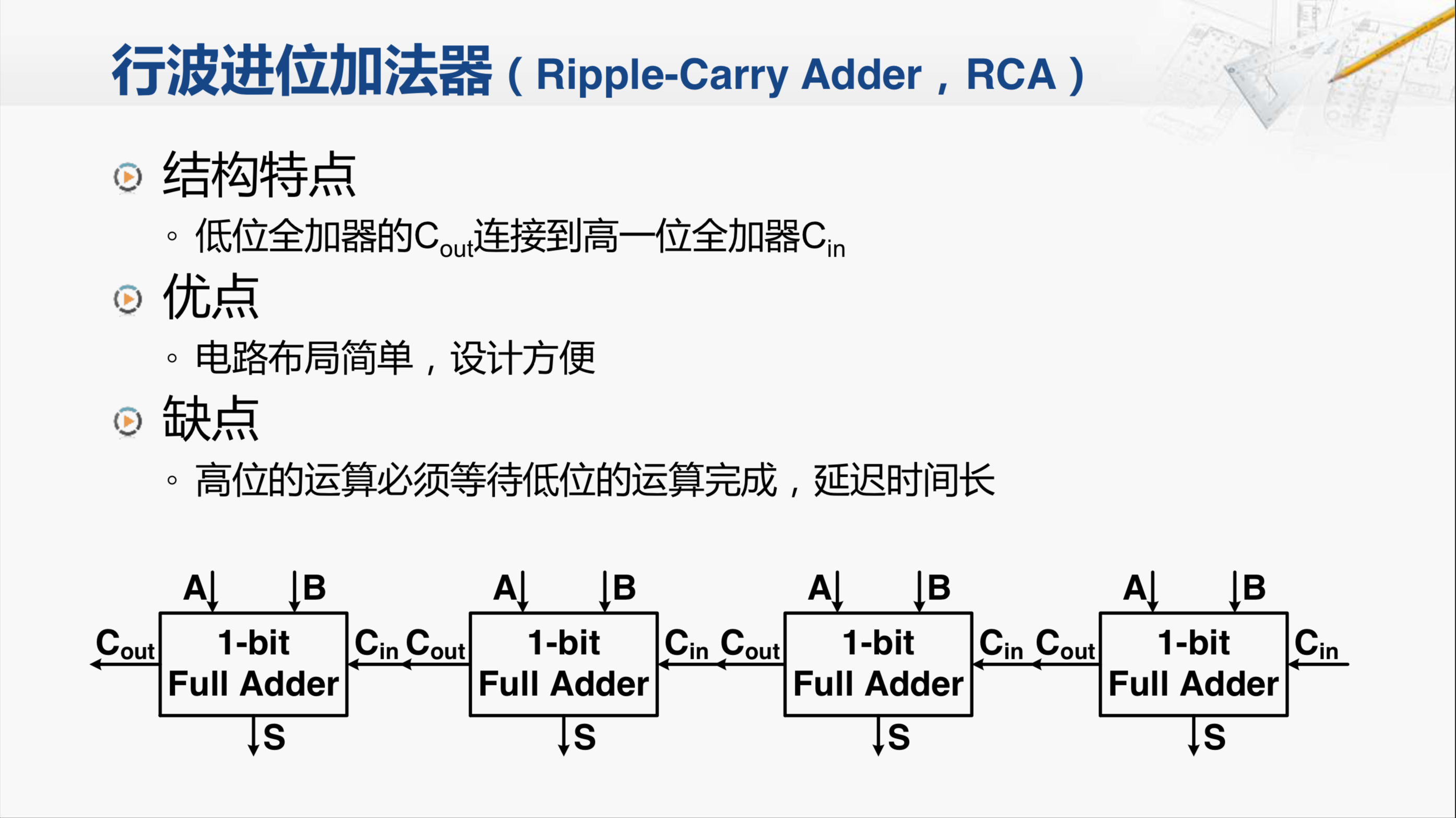
行波进位加法器，它的英文名称简称为RCA。这个加法器从结构上来看，低位全加器进位输出都连接到高一位全加器的进位输入。它的优点是电路布局简单，设计方便，我们只要设计好了全加器，连接起来就构成了多位的加法器。但这缺点也很明显，也就是高位的运算必须等待低位的运算完成，这样造成了整个加法器的延迟时间很长。因此，我们要来分析一下，这个行波进位加法器延迟的情况。

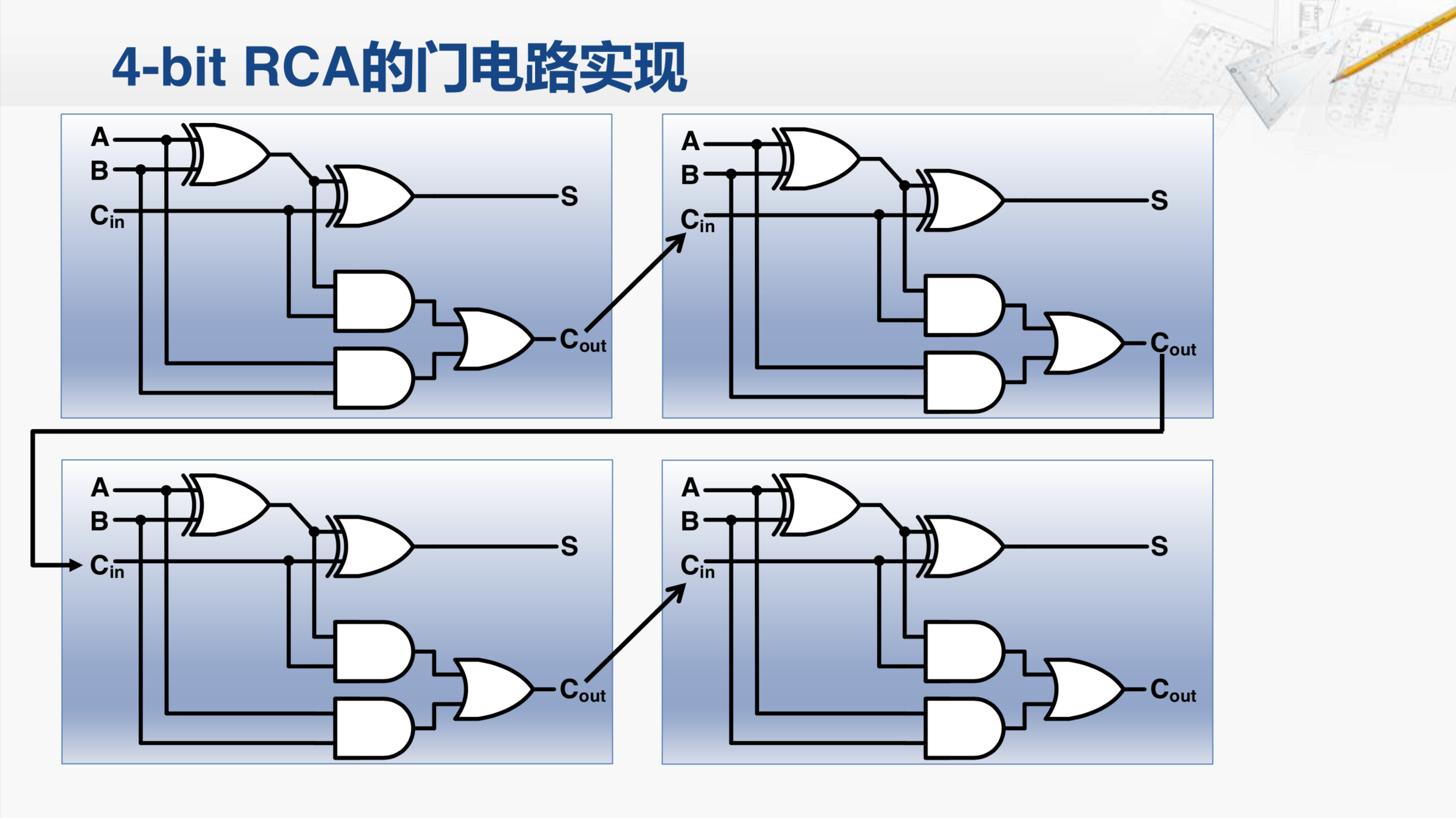
我们还是以四位的形波进位加法器为例，我们把构成这个加法器的四个全加器内部结构打开，每个全加器的进位输出连接到下一个全加器的进位输入。因此，我们现在看到的就是一个四位的行波进位加法器的门电路的实现。

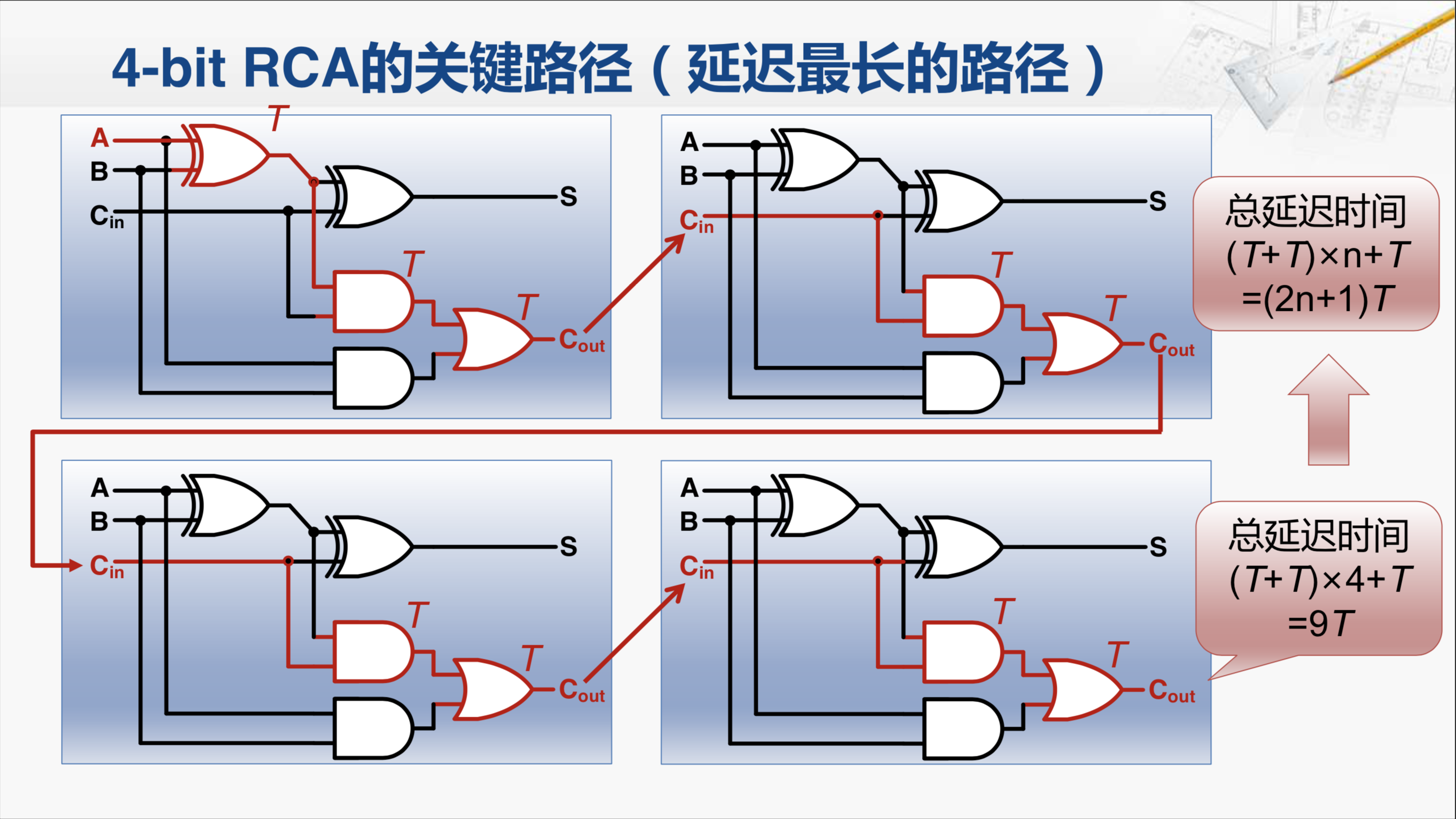
要对一个电路的性能进行分析，我们就要找出其中的最长路径，也就是找出所有的从输入到输出的电路连接中，经过的门数最多的那一条。经过分析，我们可以发现，实际上红色标明的这条路径就是这个加法器延迟最长的路径，也被称为关键路径。我们来做一个简单的分析，对于最低位的全加器，它的A、B和Cin都已经准备好。其实，输入信号进入到这块儿电路之后，在连接线上传递需要花时间，称为线延迟。而经过这样的门，也需要花时间，称为门延迟。在进行设计原理分析时，我们主要关注门延迟。因此从这条通路来看，产生第一个S输出，需要通过两个门的延迟，所以它显然不是最长的路径，因为往下，还会经过一个门， 然后再经过一个门，要经过三个门才会产生这个全加器的进位输出Cout。当然我们还要注意，为什么是从A这里来，而不是从这个与门的另一个输入，我们可以发现，这个与门的另一个输入，直接连接了Cin，所以它不如从上面来的这条路径更长。当然，从A出发或着从B出发都是一样的，所以对于第一个全加器，它的最长路径是这一条。

然后进入第二个全加器，那么等传递到这个与门的时候，我们会发现这个与门下面这个输入经过了三级门才到达（第一个全加器经过三个门）；而上一个输入，只要经过一级门就到达了，所以显然最长路径需要从下面这条通路开始计算的。然后，在这个全加器中经过两个逻辑门，产生了进位输出，依次往下传递。在每一个全加器中，都经过了两个逻辑门，最后产生了进位输出。我们要注意，在这个进位输出产生时，所有的全加器的S都已经产生了，即使最晚产生的这个S，也比这个Cout早了一级门。那如果我们把每一个门延迟都记为T的话，首先在每个全加器内部，都要经过2T个延迟，然后还要加上最开始的这一个门延迟，因此我们就可以计算出总门延迟时间就是2T乘以全加器的数量，再加上一个T。

对于四位的行波进位加法器，一共是九个门延迟，那如果是N位的行波进位加法器，那就一共是2N+1个门延迟。

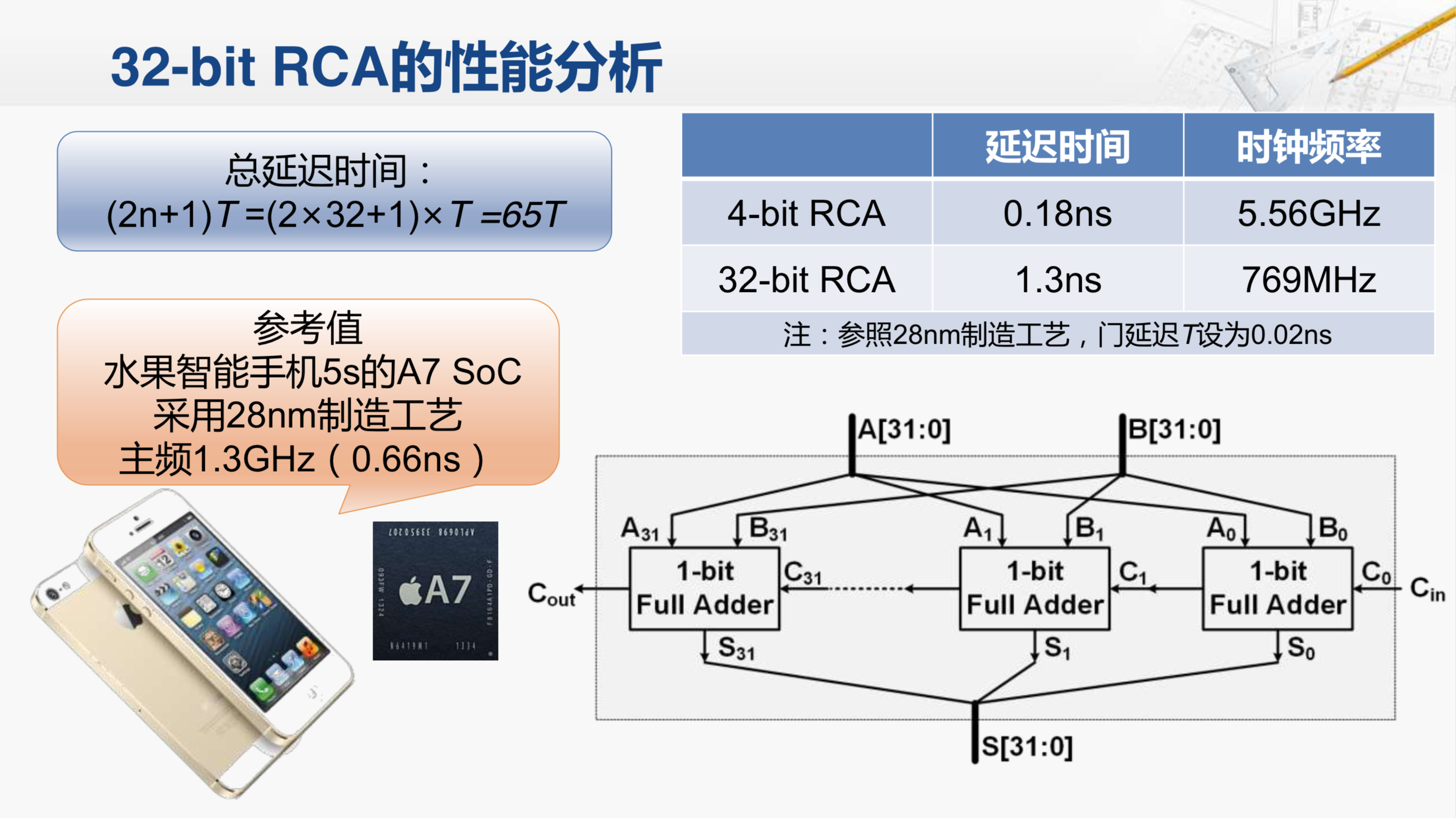
这样对于32位的行波进位加法器来说，N就等于32，所以一共是65个门延迟。那65个门延迟到底代表着什么呢？这样看起来还是太抽象了，我们选一个大家熟悉的物品，有一些感性的认识。比如说一款著名的智能手机，它内部的CPU采用着28nm的制造工艺，主频是1.3GHz，也就是时钟周期0.66ns，这就是最近的两个时钟上升延之间的时间长度。因为加法器的输入是来自寄存器，而且加法器的输出包括运算的和和进位输出，都是要传递到寄存器保存起来。所以说这些信号从前一级的寄存器，经过加法器的所有逻辑，一直到下一级寄存器的输入，不能超过0.66ns。那实际情况又是怎么样的呢？对于一个32位的行波进位加法器，如果采用28nm的制造工艺，门延迟大约为0.02ns，因为总共需要65个门（2*28+1）的延迟，所以一共需要1.3ns，这远远超过了我们所要求的0.66ns，采用这样的加法器，它的主时钟频率最多也只能达到769MHz。这里，我们都还没有考虑寄存器的建立保持时间，还有连线的延迟，实际的频率只会比这个更低。所以说，这样的加法器与我们现实中实际使用的加法器，性能差距是非常大的。那我们应该如何进行优化呢？

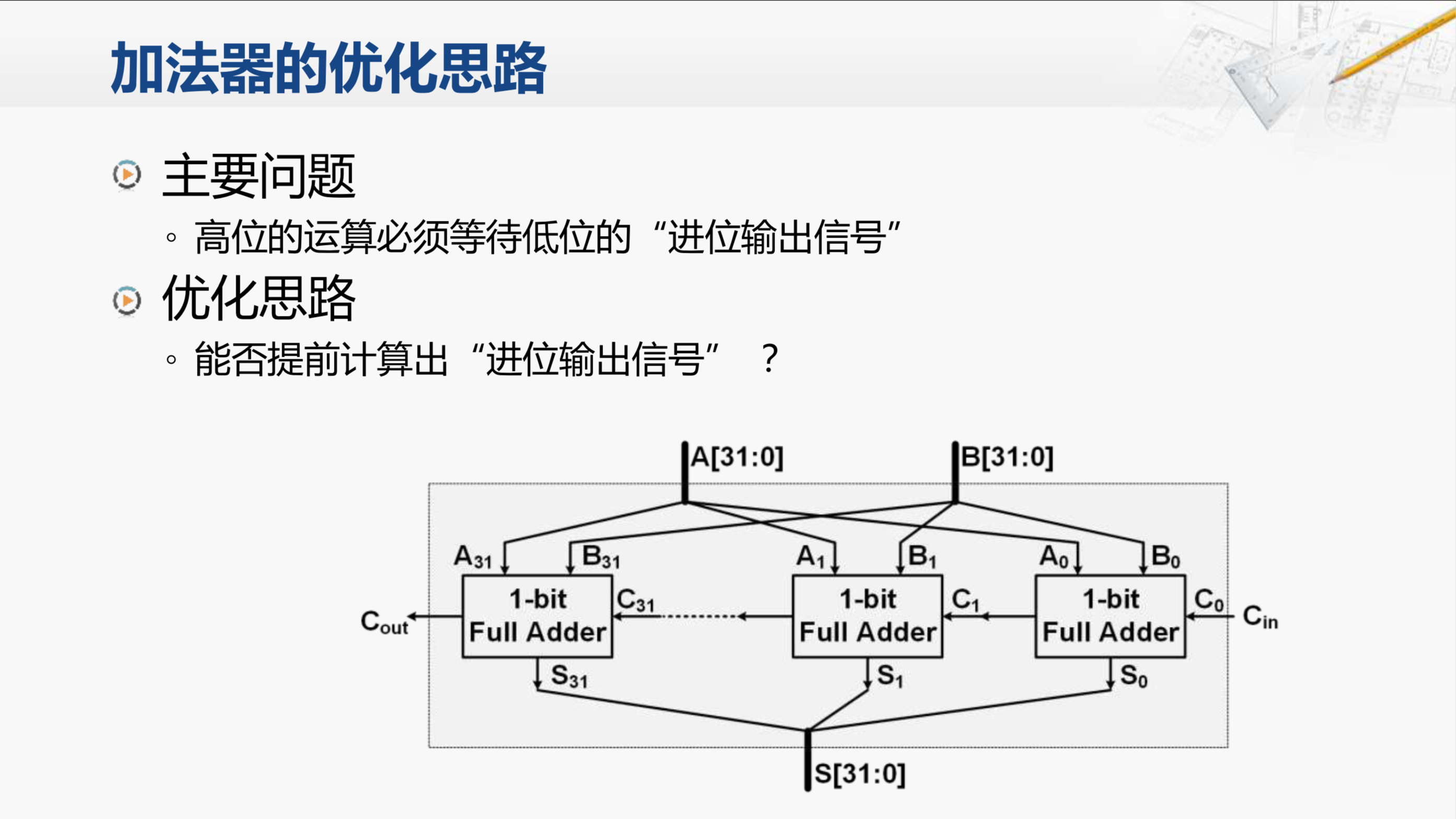
首先，还是要分析一下这个加法器的问题所在。影响性能的核心问题，就在于高位的运算必须要等待低位的进位输出信号。那我们是否可以提前计算出这些进位信号，以提高性能呢？

那我们就对进位输出信号，进行重点的分析。对于每个全加器，它的进位输出信号记为Ci+1。Ci+1可以通过这样的逻辑表达式计算出来，它的意思就是，如果这个全加器的三个输入 Ai，Bi或着Ci，只要任意其中两个为1，则进位就是1。这是很自然的，三个一位的二进制数相加，有两个或着两个以上的1，则自然会产生进位。我们再将这个算式当中的Ci提取出来，就可以得到下面这样一个表达式。在这个表达式当中，Ai和Bi都是在运算之初就是确定的，所以为了表达的简便，我们再设定两个信号，一个称为Gi，它就等于Ai和Bi的与；另一个是Pi，它就等于Ai和Bi的或。这样将Gi和Pi代入到这个算式当中，就得到了一个更为简化的算式。我们只需要记住的是，Pi和Gi是由Ai和Bi产生的，他们都是在运算之初，就可以确定了的信号。

那么通过这样一个通用的表达式，我们来看每一个进位输出信号Ci，是如何计算出来的。首先，C1是通过G0、P0和C0计算出来的。那么在运算之初，G0和P0都是已知的，C0也是已知的，所以C1不用进行任何的等待，直接就可以计算出来，而C2，是由G1、P1和C1运算而得的。在这里G和P都是已知的，但是C1不是这个加法器的直接输入，但如果我们想提前计算出C2，我们可以将上一个算式，代入到这个算式当中，也就是C1转换成上一个算式，我们再将这个算式展开，除了G和P之外，只有C0，所有的信号都是在运算之初就可以确定的，这样，我们就不用等待最低位的全加器产生C1，而是通过整个加法器的输入，直接计算出C2。与之类似，原本C3也要等待C2的运算，那么现在将C2这个算式带进来，变成这样，然后再进行展开，展开后的算式中除了G和P也只有C0，所以所有的信号也都是在运算之初就可以确定的了。同样，我们还可以得到C4，越高位的进位输出信号，就越复杂。但是我们可以看到，C4的算式当中，除了G和P之外，也只有C0，所以它也不用依赖低位的进位信号。通过这样的转换，我们就有了提前计算所有的进位输出信号的方法。那它在硬件上是如何实现的呢？

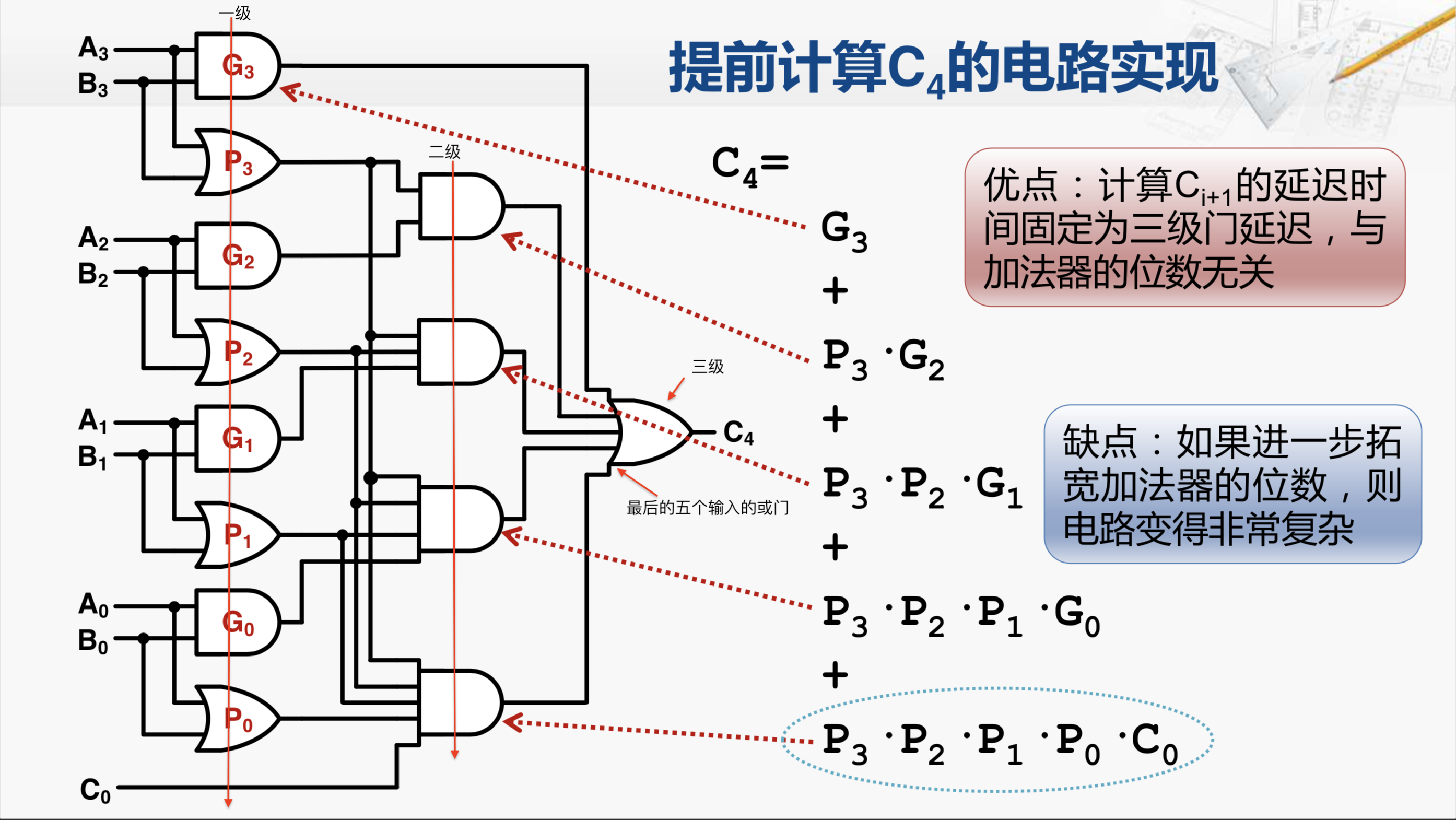
我们以C4为例，我们将刚才C4的这个表达式写成竖排的形式，它对应的硬件电路是这样的。我们可以看到，最外层一共有五组元素进行或运算，对应了最后的这个五输入的或门。

而其中第一个元素是G3，G3就是A3和B3的与，所以在这里我们可以看到，A3和B3经过了一个与门，与门的输出直接连到了最后的这个或门上。

第二个元素是P3和G2的与，它就对应了这个与门，其中一个输入是P3，而P3是A3和B3的或。另一个输入是G2，G2是A2和B2的与。

再往下看，第三组元素对应了这个3输入的与门。第一个输入是P3，来自于这里。第二个输入是P2，来自这里。第三个输入是G1，来自这里。

依此类推，就可以得到第四组元素，第五组元素。这样我们就可以发现C4只需要通过A，B和C0就可以计算出来，而且计算C4的延迟只需要三级门，这是一级，这是第二级，这是第三级。其实由此类推，计算任意一级的进位输出都只需要三级门延迟，与加法器的位数无关。但只是如果进一步拓宽加法器的位数，最后的算式会变得越来越长，对应的电路就会变得越来越复杂。那先不谈这个缺点，至少我们有了提前计算进位输出的方法，用这样的方法实现了加法器就被称为超前进位加法器，它的英文缩写也可以写成CLA。

这就是一个四位的超前进位加法器。它仍然由四个全加器构成，但是每个全加器的进位输入并不来自于前一级的全加器，而是来自一个统一的逻辑，图中紫色这就是刚才我们展示的超前进位的逻辑。对于每一个进位，其实都只需要三级门延迟就可以计算出来。然后进入到全加器当中，还需要经过一级门延迟才可以计算出对应的S信号。因此，对于超前进位加法器总的延迟时间为4级的门延迟。而四位的行波进位加法器总延迟时间为9级的门延迟。这个性能的提升就是非常可观的。

而且更为重要的是超前进位加法器它的门延迟与加法的位宽是没有关系的，所以对于32位的加法器如果采用行波进位的方式，我们已经分析过需要65级的门延迟，那如果采用超前进位的方式，理想情况下也只需要四级的门延迟。但可惜的是，这也只是一个理想，因为要实现32位的完全的超前进位，电路就会变得非常的复杂。我们可以看一看C31的超前进位的表达式就会变成这个样子，也许这样就需要32输入的与门和32输入的或门。这个在实现上就不太可行了。因此通常的实现方法是采用多个小规模的超前进位加法器拼接而成一个较大的加法器，比如说，要生成一个32位的加法器，我们可以先做一个8位的超前进位加法器，然后将四个八位的超前进位加法器用行波进位的方式连接起来，从而构成一个32位的加法器。那么这样分析，一个32位的行波进位加法器它的门延迟是1.3个ns，而一个超前进位加法器只需要0.08个ns，也就是四级门延迟。如果我们采用四个超前进位加法器拼接成一个32位的加法器，那也只需要0.26ns。这个0.26ns是怎么算出来的呢？就留给大家自己来计算了。那么因为这个加法器的关键路径是0.26ns，那么它就可以运行在3.84GHz的时钟频率下，那么至少它就不会成为我们整个复杂的CPU设计的关键路径，不会降低整个芯片的使用频率了。

这个经过改进的加法器，不仅功能正确，而且在性能和可实现性两个方面达到了比较好的平衡。那现在把它和之前实现的逻辑运算部件整合在一起，就构成了一个ALU可以提供基本的算术运算和逻辑运算的功能了。