4.5 加法和减法的实现
计算机组成
4 算术逻辑单元
4.5 加法和减法的实现

加法和减法是两种基本的算术运算。计算机进行二进制的加减法的运算和我们平时用纸笔进行的运算方法肯定是不一样的。那它是如何实现的呢?让我们一起来分析。
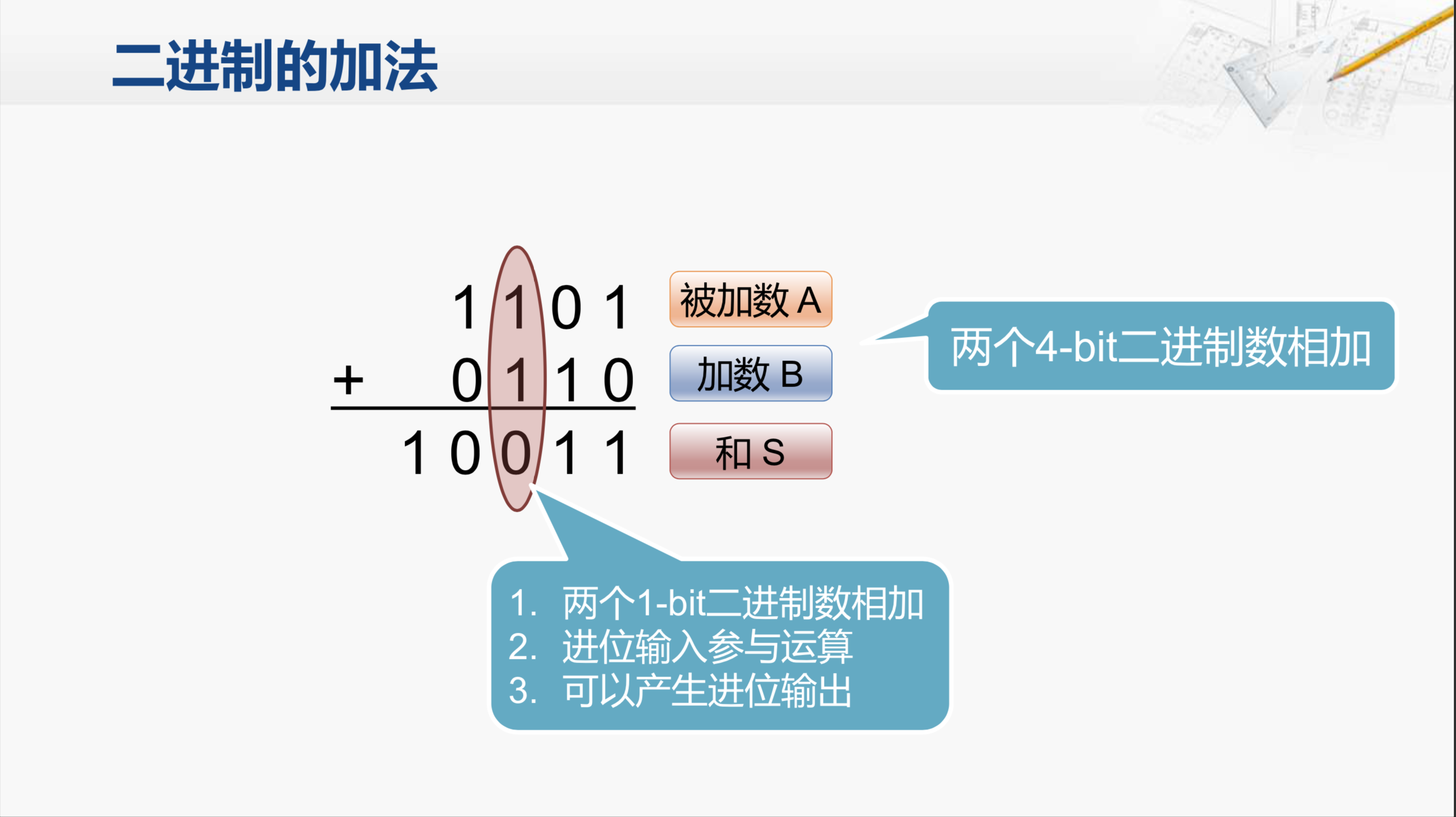
我们先来看如果用手工运算的话如何进行二进制加法的。这里有两个四位数的二进制数相加,被加数是1101,加数0110。其实和我们做十进制的加法是一样的,首先从最低位开始,1加0等于1;然后第二个0加1等于1;第三个1加1,因为我们是二进制就是逢二进一,所以这里应该计为0并有一个进位,我们暂且记下,然后再算最高位,最高位1加0本来应该等于1,还要加上一个进位,所以应该等于0,再往上进一位,10011 这就是最后的(和)。因此,对每一位的相加来说实际上要做这么几项工作,我们要完成两个一位(1-bit)的二进制数的相加,而且可能有从低位传递过来的进位要参加运算,最后还有可能产生进位的输出。
那么现在就来看两个一位(1-bit)的二进制数的相加是如何用硬件电路实现的。
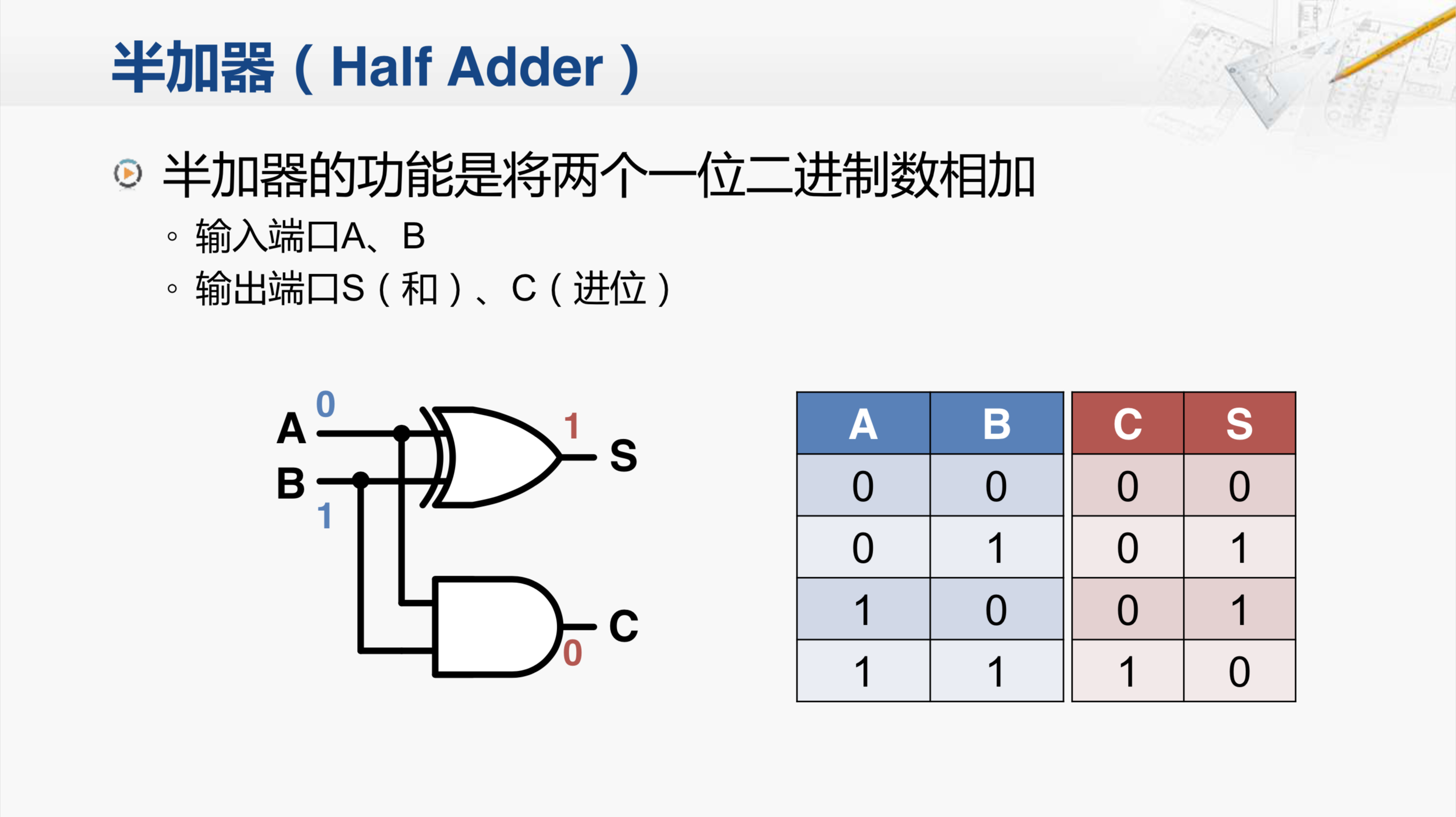
首先我们来介绍一个电路叫半加器,半加器的功能是将两个一位的二进制数相加。这就是半加器,由一个异或门和一个与门组成。它有两个输入端口 A 和 B ,就是我们要相加的两个一位二进制数。两个输出端口其中一个是S,相当于这两个一位二进制数相加对应产生的(和);而C则是它们产生的进位,有进位就是1,没有进位就是0。
那如果A等于0,B等于1那经过这个异或门之后的输出应该是多少呢?我们知道对于异或门如果两个输入是不相同的,那输出为1;两个输入是相同的时候输出为0。所以,这个时候(A等于0,B等于1)输出应该为1。而下面这个与门只有两个输入都为1时,输出才是1。 那么这时(A等于0,B等于1),输出应该是0。这个结果也正好符合我们对这两个二进制数进行相加所得的和及进位。
那么对于A、B来说总共有四种情况的组合,对应产生四种运算结果。除了我们刚才介绍的A、B为0、1的情况。我们可以再来看当A、B均为1时,这时候运算的结果是十进制的2,也就是二进制的 10 ,所以对应S这位的和是0 ,产生一个进位1。
这就是半加器,但半加器相比我们刚才提到的功能需求还差一点,它不能将低位产生的进位作为输入参与运算,所以我们还需要增加这个功能。
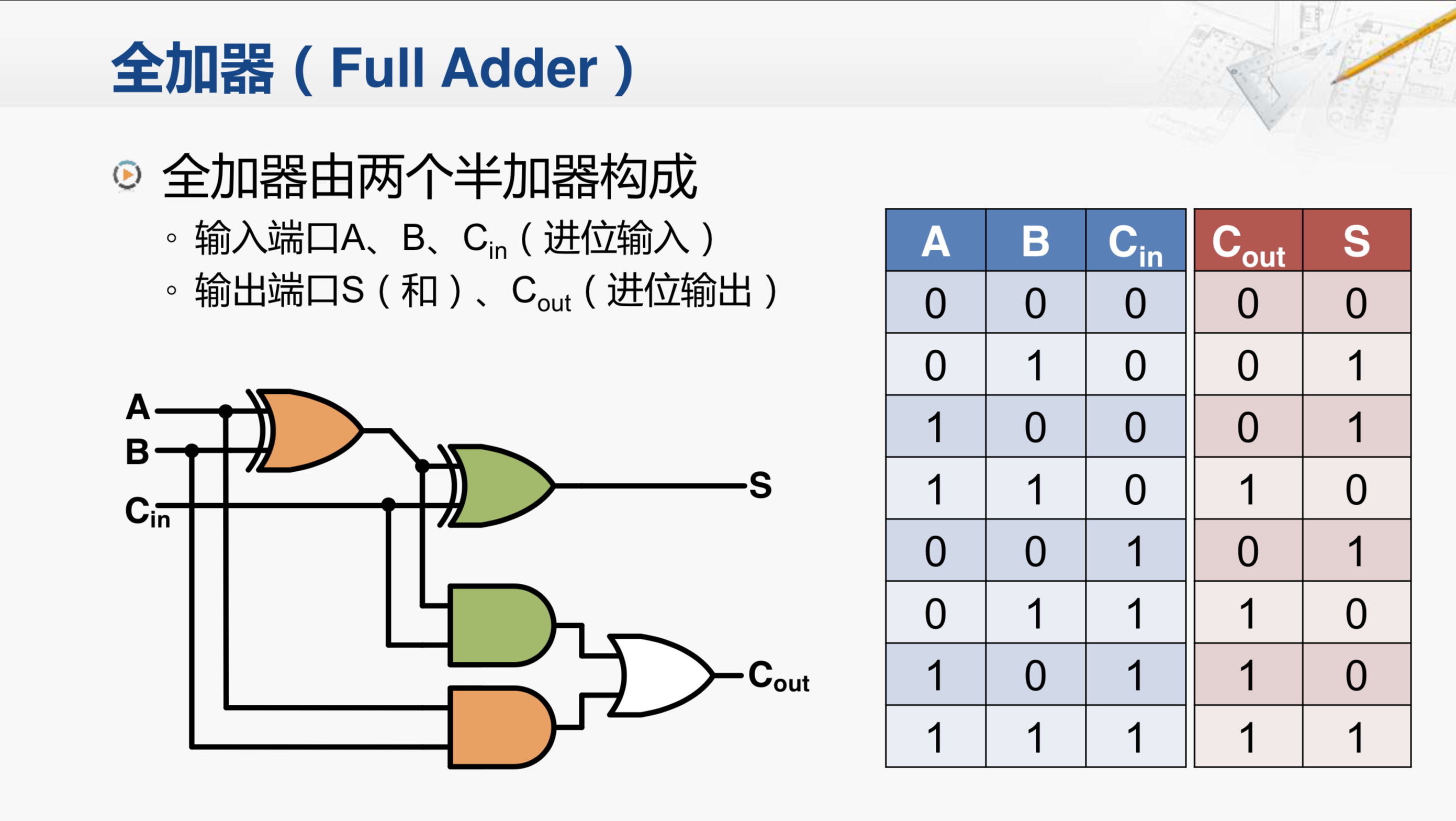
这就是全加器,实际上全加器是由两个半加器构成的。这个图中这两个绿色的异或门和与门就是一个半加器,而这两个橙色的异或门和与门是另一个半加器,最后再添加一个或门就构成了全加器。
这个全加器有三个输入,除了两个原操作数A和B,还有一个进位输入Cin。它的输出则有两个,运算结果S和进位输出Cout。这样三个输入总共有8种组合的情况,上图右边是它们对应的输出,我么来看其中的一个例子。比如A和B均为1并且进位输入也是1的时候,相当于三个1相加,用十进制来说运算结果就是3。那么当前的位S和进位Cout组合在一起,我们可以看到 二进制的11实际上也就是十进制的3,这样全加器就能满足我们刚才分析的那三点要求。

那我们再回到刚才那个例子,来看看如何用全加器构成一个4比特的加法器。这是一个全加器,我们将四个全加器串联起来,前一个全加器的进位输出连到后一个全加器的进位输入,这样就构成了一个四位的加法器。那这个四位的加法器是如何工作的呢? 我们还是通过这个例子来看,A有四个二进制位,我们用橙色来表示;B也有四个二进制位,我们用蓝色来表示。在运算时,需要将A对应的二进制位连到这四个全加器的A输入端口,而将B对应的四个二进制位连到这四个全加器的B端口,我们用不同的颜色标出来。
对于整个加法器的进位输入我们设为0(即最右边Cin为0),这样最右边全加器的三个输入都已经确定,很快就可以得到输出,S为1,Cout则为0。这样第二个全加器的三个输入也都已经确定,从而可以产生对应的输出。接下来S是1,进位是 0。对于第三个全加器,这时候三个输入也已经确定了,这时候因为有两个1相加,所以S应该是0,进位是1。对于最后一个全加器,运算结果S是0,Cout是1。这样作为一个整体,这个四位的加法器就得到了运算的结果,包括两个部分:
一部分是用S的端口出来的, 作为这个运算的(和)。
还有一部分是从最左边的Cout出来,作为整个加法器的进位。
因此,这个四位二进制数的运算结果就包括进位C和和S这两个部分。
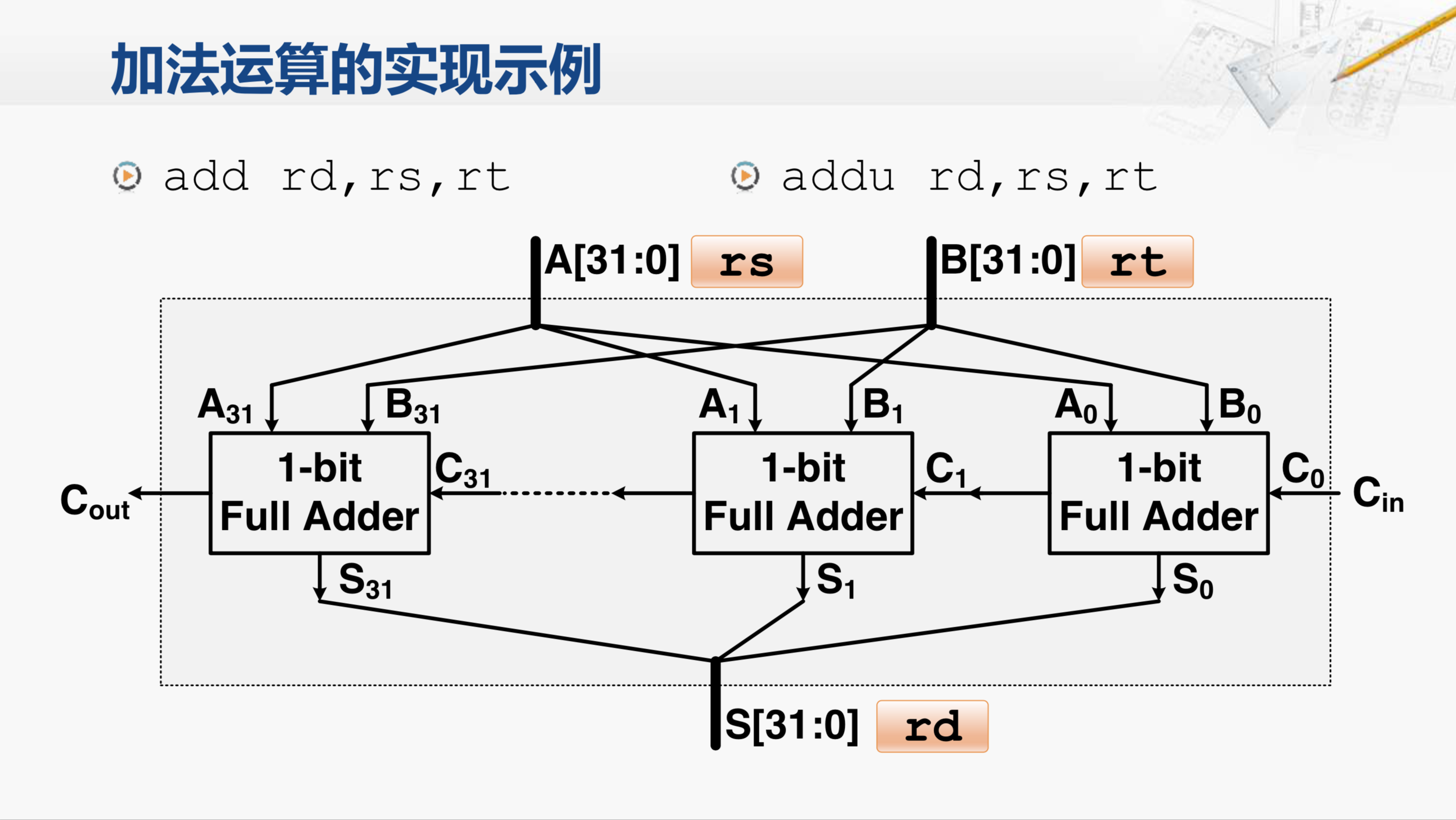
和这个四位的加法器一样,我们可以很容易的构建出32位的加法器,也就是用32个全加器串联而成,它的输入是两个32位数A和B,在加法器的内部会分别连接到了32个全加器的A输入端口和B输入端口。所有全加器的输出成为一个32位的加法器的输出。整个加法器的进位输入(最右边的Cin)连接到了最低位(最右边)的全加器,而最高位全加器的进位输出(最左边Cout)作为整个加法器的进位输出,这样的加法器就可以满足加法运算指令的需求。
对于 add rd, rs, rt 这条指令,我们只需要将rs所指向的寄存器和rt所指向的寄存器的内容分别连接到A端口和B端口,并将S送到rd所指向的寄存器,这就完成了对应的加法运算。那么与add指令类似,addu指令也完成了同样的运算功能,这两条指令的区别就在于对溢出的处理不同。

溢出是指运算结果超出了正常的表示范围。由于在计算机中我们总是用有限的二进制位来表示一个数,因此加法运算的结果有可能或超出这个有限的位数所能表示的范围。溢出这种情况仅是针对有符号数运算来说的。具体表现就是如果两个正数相加,结果变成了一个负数;或者两个负数相加结果变成了一个正数,这显然是不正确的,这种情况就是由溢出造成的。
我们来看一个例子,0011加上0101如果用个四位加法器进行运算,就会得到1000。如果我们把它们都看成无符号数那么0011就是3,0101就是5,而1000就是8,那么这个运算结果是正确的。但如果我们把它看作有符号数,原操作数仍然是3和5,但是运算结果1000,它其实代表的是-8。这样子的结果就是不正确的,也就是发生了溢出。
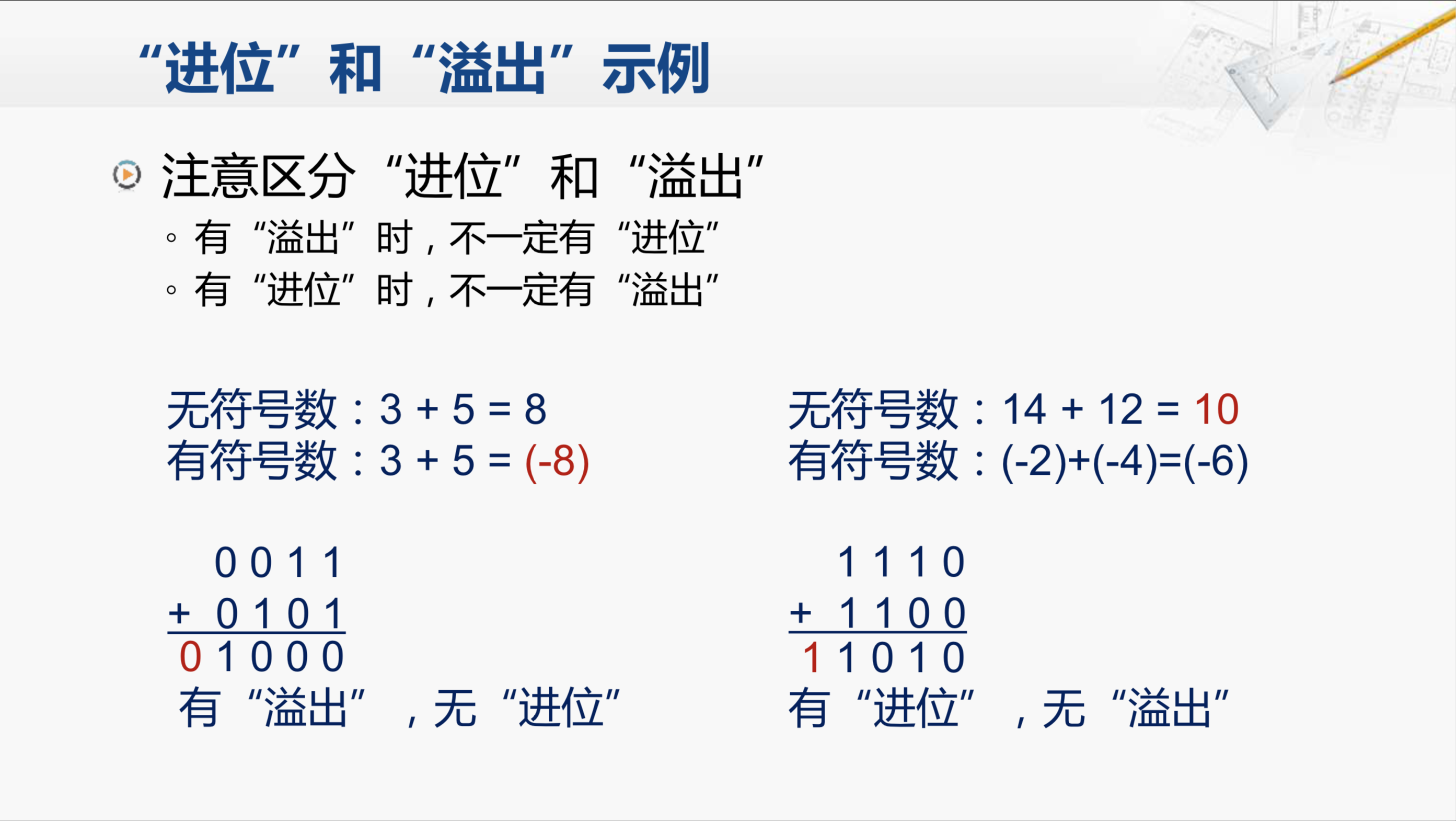
那么还需要注意的是进位和溢出的差别:有溢出的时候不一定有进位,而有进位的时候也不一定有溢出。我们分别通过例子说明:
左边这还是刚才这个例子,这个例子中的加法实际上是没有发生进位的,所以这就是一种有溢出无进位的情况。
我们再看一个例子:1110加上1100,送到四位的加法器中运算的结果1010,同时有一个进位1。这显然是有进位,但它却是无溢出的情况。为什么呢?我们来看,如果把它当作无符号数进行运算1110是14,1100是12。如果带上进位一起考虑那就是正确的运算结果26;如果不带进位则是为10,因为四位的二进制位只能表示小于16的数,所以无符号数的的运算结果可以默认为对结果进行模16的运算,那只看着结果中1010四位的话结果是10,相当于26模16的值,所以这也是正确的。而对于有符号数来说相当于-2加上-4,而1010这四位的结果就是-6,这个运算也是正确的。
当然,从另一个角度来看,因为溢出是针对有符号数的运算结果超出了能表示的范围,我们也可以把有进位这种情况看作无符号数的运算超出了能够表示的范围。但是进位是很容易判断的,加法器本身就提供了这样的机制,最高位的全加器的进位输出(最左边Cout)就是整个加法器的进位。那溢出又该如何判断呢?
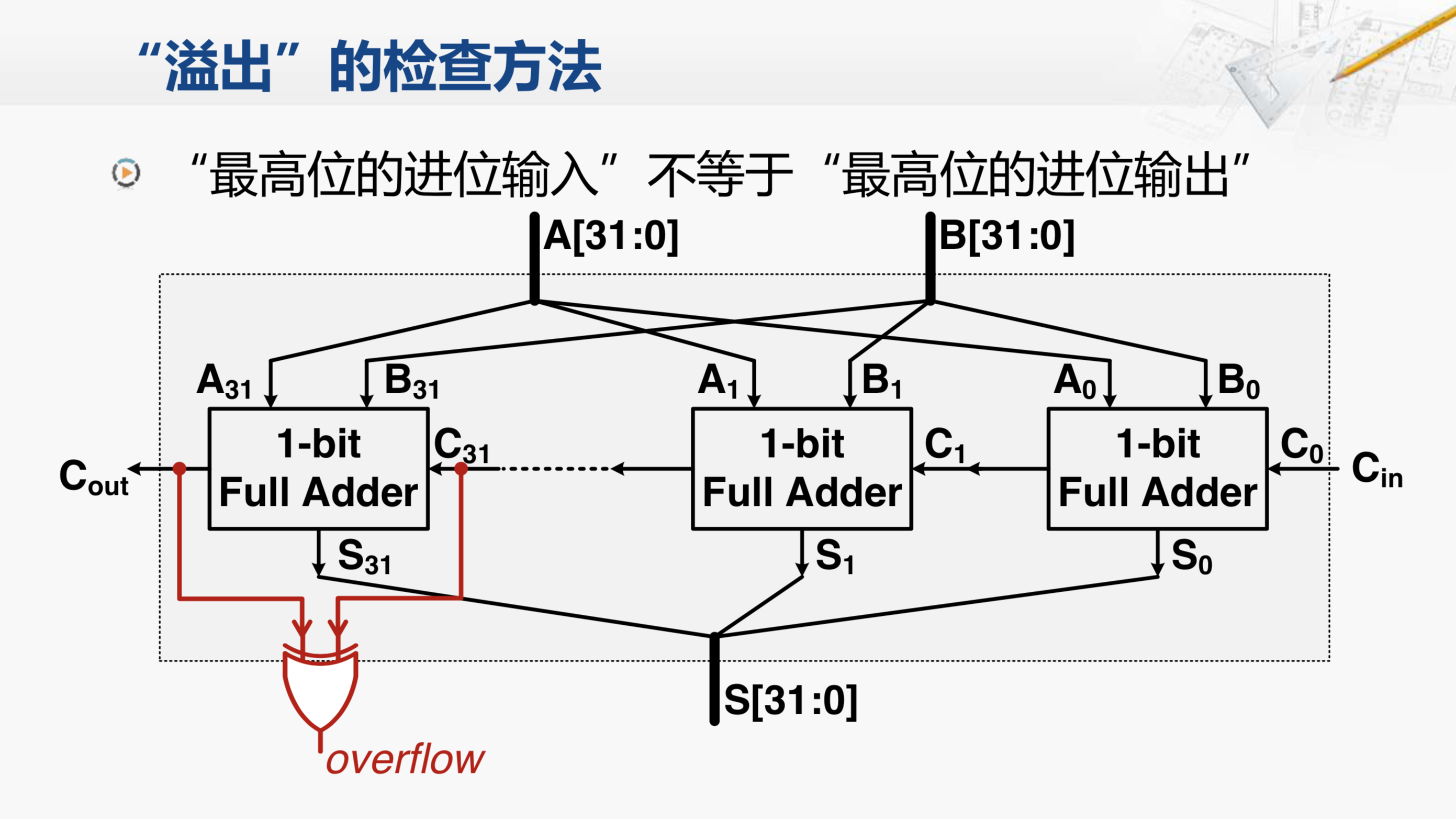
其实很简单,就是当最高位的全加器的进位输入不等于它的进位输出的时候,这就是发生溢出了。这是刚才的全加器,这个C31就是最高位的全加器的进位输入,Cout就是最高位全加器的进位输出,把这两个信号连出来,判断它们是否不相等。那么用什么方法来判断不相等呢?其实非常简单,连接一个异或门就可以了。当它们不相等时,异或门的输出为1;当他们两个都为0或者都为1时,异或门的输出为0。因此,就可以用异或门的输出这个信号来表示是否发生了溢出。至于为什么用这个方法就可以判断溢出,留给大家自己思考。然后还需要说明的是,对于一个加法器的硬件实现,它并不关心这两个输入数是有符号数还是无符号数;或者说,它对于有符号数和无符号数的处理都是一样的,全都是通过这套同样的硬件逻辑进行运算,产生相同的结果。至于参与运算的数到底是有符号数还是无符号数,取决于编程人员如何去看待它。因此,是不是要处理溢出以及如何处理溢出,就不能只交给硬件来做,不同体系结构有不同的方法。
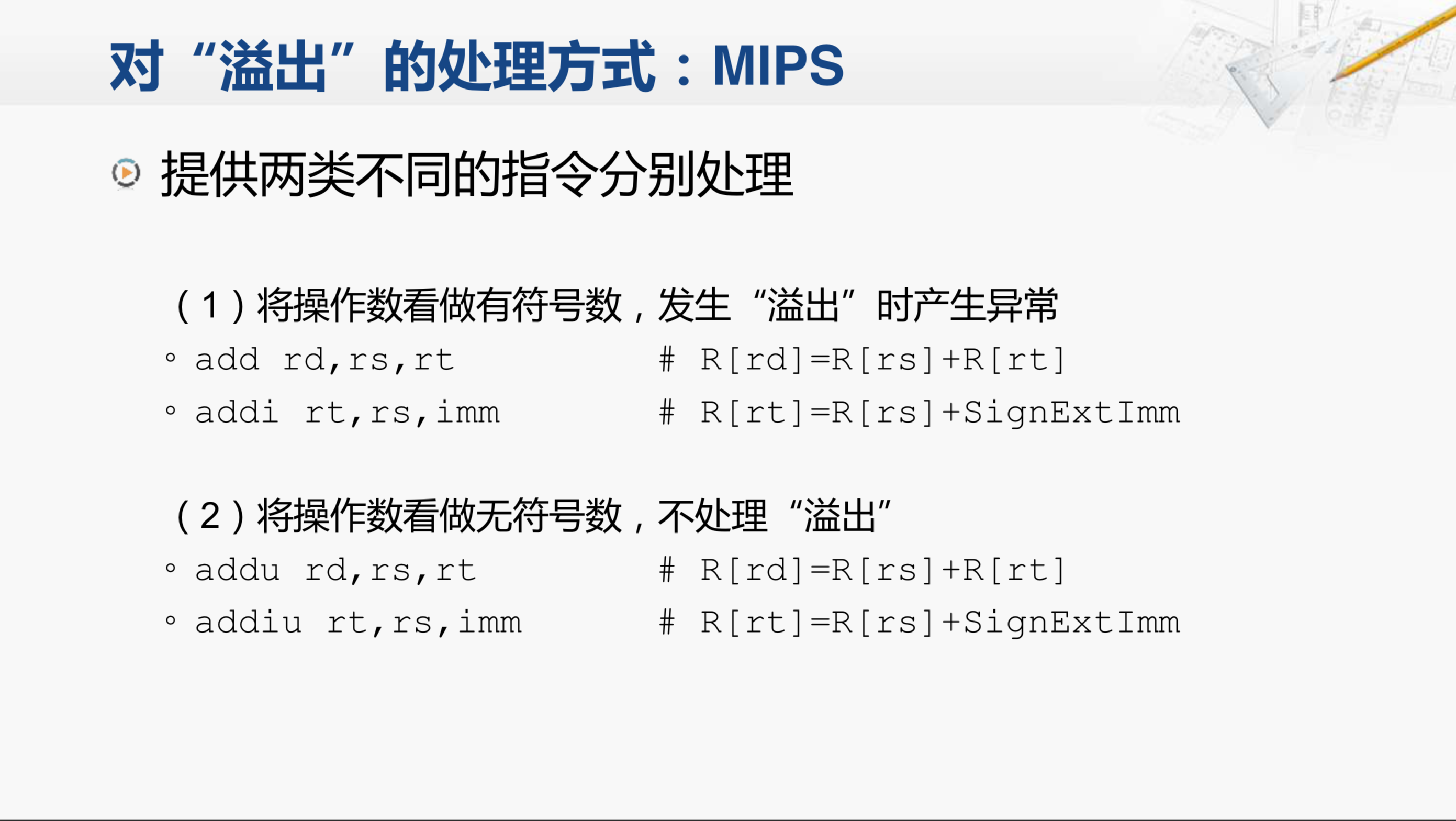
我们先来看MIPS处理溢出的方式,它提供了两种不同的指令。
如果编程人员想将操作数看作有符号数需要处理溢出,则需要使用add和addi这样的指令。当这样的运算发生溢出时,会产生异常。就是说,控制电路会检查加法器产生的overflow的信号,如果overflow信号有效,控制电路就会当做一个异常的情况进行处理,至于如何处理,我们会在讲到中断和异常时再做分析。
如果编程人员希望将操作数看作无符号数,也就是不对溢出进行处理,那就需要使用addu和addiu这两条指令,它们分别和上面的那两条指令是对应的,唯一的区别就是在执行这两条指令时,控制电路不会检查加法器输出的overflow信号。
所以说,MIPS处理溢出的方式是提前做准备。按照是否要处理溢出,采用不同的指令进行运算。
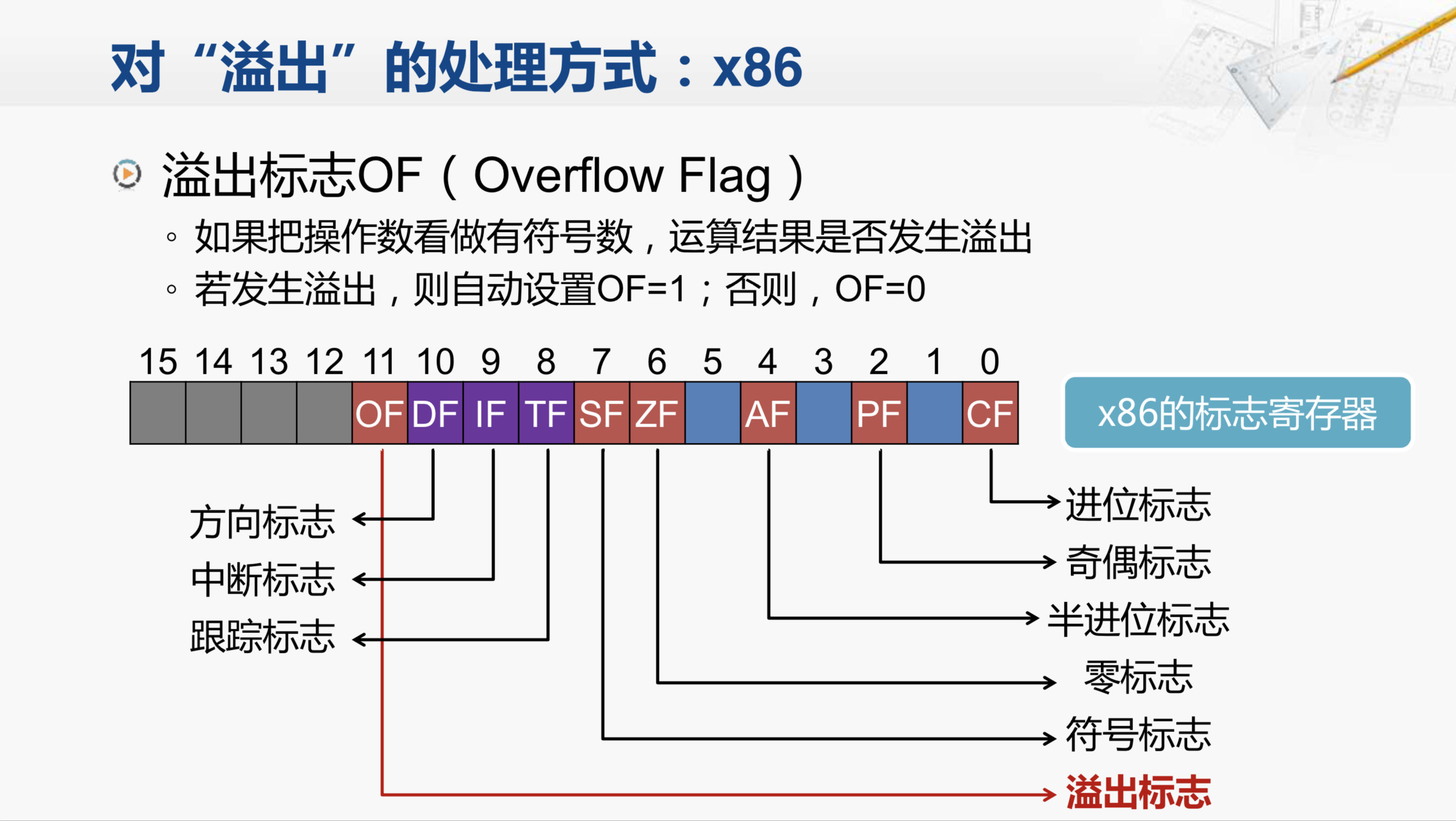
而x86则采用了另一种方式,它并没有根据是否处理溢出分为两种运算指令,x86的运算指令如果产生了溢出,并不会直接由控制电路检查到并进行处理。而是将加法器产生的溢出信号传送到了标志寄存器,如果发生溢出,则会置标志寄存器当中的OF位为1;如果没有发生溢出,则置OF位为0。这就是x86的标志寄存器,其中第11位是OF位,溢出标志。如果想对溢出进行处理,则在后续的指令中需要检查标志寄存器的OF位是否为1并进行相应的操作。

最后我们再来看一看减法运算。其实减法是可以很容易的转换为加法的,例如我们要进行A-B的运算,那就相当于进行A加上负B的运算,但我们需要注意的是,我们如何将B转换为负B呢?我们知道计算机当中使用补码来保存二进制数的。B转换为负B,可不是在前面加一个负号这么简单。那么补码表示二进制数取相反数,有这样一个转换的规则:叫做按位取反,末位加一。这是什么意思呢?我们来看一个例子:
例如我们有一个数X,那么所谓按位取反,就是将X中的每一位由0变成1,由1变成0,那么得到了X按位取反以后的值,如果我们把这两个值相加,那么它们的和,显而易见,每一位都是1,在补码表示中,全1的这个二进制数就代表着-1。那么由这个运算我们可以得到,如果将X和它按位取反后的值相加就等于-1,我们把这个等式进行一些变换,就可以得到X的相反数就等于对X进行按位取反,然后再加上1。
那么我们在加法器的基础上,用这样的方式就可以很容易的实现减法器。 也就是A减B,相当于A加上负B,实际上就等于A加上B的按位取反然后再加1。那么我们应该对加法器进行怎样的改造就能实现这样的操作呢?
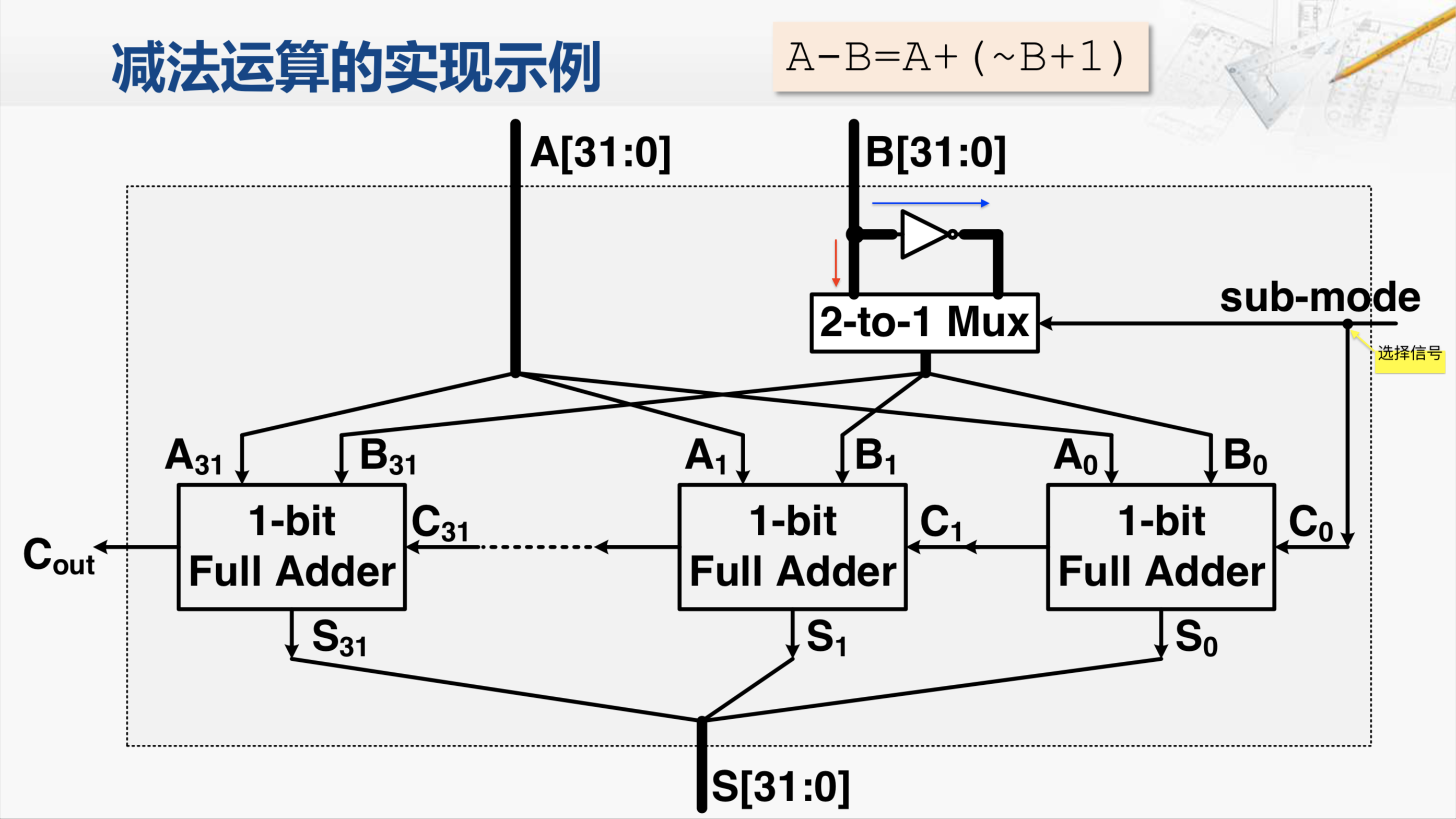 我们来看,这就是刚才的那个加法器。原来的输入A和B都不变,我们增加了一个新的输入,只有一个比特,称为减法模式(sub-mode)。它首先控制了一个二选一的多选器,如果这个信号为0代表是执行加法操作,那么会将多选器的红色箭头指示的这条通路选通,也就是直接将B传送到下面的这些全加器,这就跟刚才的加法运算是一样的,而且我们还注意到sub-mode的选择信号还连接到了最低位全加器的进位输入C0,但是因为它现在是0,所以仍然和刚才的加法操作是一样的,这时候就在执行一个加法的运算;如果sub-mode的选择信号为1,代表要执行一个减法的运算,那二选一的多选器会选择蓝色箭头这条通路,将B这个信号的输入每一位都接上一个非门,相当于按位取反,将按位取反的B送到每一个全加器与A相加。我们还要注意,因为选择信号为1,所以最低位的全加器的进位C0输入也是1,这样就实现了对B进行按位取反,末位加1的操作,于是这个加法器也就变成了减法器。
我们来看,这就是刚才的那个加法器。原来的输入A和B都不变,我们增加了一个新的输入,只有一个比特,称为减法模式(sub-mode)。它首先控制了一个二选一的多选器,如果这个信号为0代表是执行加法操作,那么会将多选器的红色箭头指示的这条通路选通,也就是直接将B传送到下面的这些全加器,这就跟刚才的加法运算是一样的,而且我们还注意到sub-mode的选择信号还连接到了最低位全加器的进位输入C0,但是因为它现在是0,所以仍然和刚才的加法操作是一样的,这时候就在执行一个加法的运算;如果sub-mode的选择信号为1,代表要执行一个减法的运算,那二选一的多选器会选择蓝色箭头这条通路,将B这个信号的输入每一位都接上一个非门,相当于按位取反,将按位取反的B送到每一个全加器与A相加。我们还要注意,因为选择信号为1,所以最低位的全加器的进位C0输入也是1,这样就实现了对B进行按位取反,末位加1的操作,于是这个加法器也就变成了减法器。
这样我们通过这个改动。这个功能部件又能实现加法,又能实现减法,通过选择信号来进行选择。

我们已经实现了加法器和减法器。那现在是否可以构造出一个完整的ALU呢?先别着急!对于计算机系统来说,我们不仅要求它功能正确,而且希望有着更好的性能。那么这个加法器和减法器是否还有更大的提升空间呢?我们下一节进行分析。

