题解
最近模拟赛抽象题太多了,让他们聚一聚
T1 多校A层冲刺NOIP2024模拟赛18 T3 DBA
暴力比较显然,直接数位dp就好,记搜的复杂度是\(O(n^4)\)的,用递推加前缀和优化可以优化为\(O(n^3)\),但我还是不理解\(O(n^3)\)凭啥能\(拿97pts\),虽然和正解没啥关系,但还是放一下记搜的代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2000+5,p=1e9+7;
int n,m,a[N];
int x,y,z,l,r,k,t;
int dp[N][15000],ans,tot;
//dp[i][j]表示截止到第i位,和为j的方案数
int dfs(int pos,int sum,bool limit){
if(pos>n){
if(sum==tot)return 1;
else return 0;
}
if(sum>tot)return 0;
if(dp[pos][sum]!=-1&&(!limit))return dp[pos][sum];
int lim=limit?a[pos]:m-1,res=0;
for(int i=0;i<=lim;i++){
res+=dfs(pos+1,sum+i,limit&&i==lim);
}
dp[pos][sum]=res%p;
return res%p;
}
signed main(){
freopen("dba.in","r",stdin);
freopen("dba.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>m>>n;
memset(dp,-1,sizeof dp);
for(int i=1;i<=n;i++)cin>>a[i],tot+=a[i];
cout<<dfs(1,0,1)-1<<endl;
return 0;
}
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2000+5,p=1e9+7;
int n,m,fac[N*N],inv[N*N];
int x,y,z,l,r,k,t,sum;
int ans,tot,a[N];
inline int quickpow(int a,int b){
int res=1;
while(b){
if(b&1)res=res*a%p;
b>>=1;
a=a*a%p;
}return res;
}
void iint(){
fac[0]=1;
for(int i=1;i<=n*m;i++)fac[i]=fac[i-1]*i%p;
inv[n*m]=quickpow(fac[n*m],p-2);
for(int i=n*m-1;i>=0;i--)inv[i]=inv[i+1]*(i+1)%p;
}
inline int C(int n,int m){
if(n<m)return 0;
return fac[n]*inv[n-m]%p*inv[m]%p;
}
inline int slove(int a,int w){
int res=0;
for(int i=0,f=1;i<=a&&i*m<=sum;i++,f=-f){
res+=f*(C(sum-i*m+a,a)-C(sum-w-i*m+a,a)+p)%p*C(a,i)%p+p;
}return res%p;
}
signed main(){
freopen("dba.in","r",stdin);
freopen("dba.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>m>>n;
iint();
for(int i=1;i<=n;i++)cin>>a[i],sum+=a[i];
for(int i=1;i<n;i++)ans+=slove(n-i,a[i]),sum-=a[i];
cout<<ans%p<<'\n';
return 0;
}
T2 多校A层冲刺NOIP2024模拟赛18 T4 银行的源起
首先讲一下\(O(n^2)\)的做法。
先考虑如果只有一个银行,有一个比较一眼但又不太好想到的性质即为:对于每条边将树分为两部分1,2,如果要想让其最优,要么1中的点全都通过这条边跑到2,要么2中的点全都通过这条边跑到1,即对于每条边的贡献为\(e[i].w*min(size[x],totsize-size[x])\),这样可以保证让每条边的贡献是最优的,推广到全局即能保证答案最优,这样就可以\(O(n)\)求解最小代价。
考虑两个银行怎么做,如果有两个银行,那么有一条边肯定是不会被任何点经过的,那么原图就被分成了两个部分,这两个部分都只有一个银行,可以直接\(O(n)\)求解,具体如图:
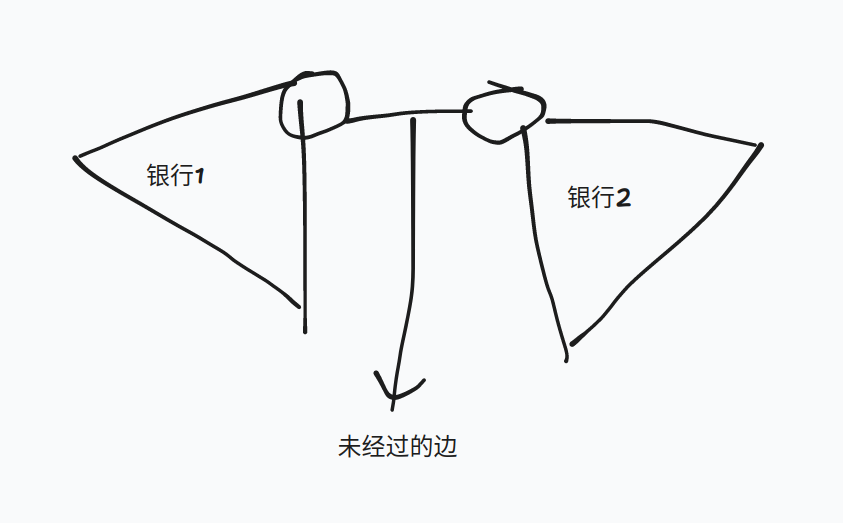
直接枚举哪条边未被经过即可,复杂度\(O(n^2)\)
既然我讲了\(O(n^2)\)做法,那正解肯定和它有点关系,考虑如果要想保证答案正确性,枚举那条边未被经过这个过程肯定不能少,那只能考虑去优化求解贡献的过程,这个时候看这个式子是带着\(min\)的,考虑拆开分类讨论一下:
当\(size[x]>totsize/2\)时贡献为\(e[i].w*size[x]\),反之\(size[x]<=totsize/2\)贡献为\(totsize*e[i].w-size[x]*e[i].w\),观察到贡献是和\(size[x]\)紧密相关的,可以直接开一个以\(size\)为下标的权值线段树,查询贡献时直接找到\(size=totsize/2\)的位置,左边,右边分别算贡献即可。
考虑线段树要维护什么信息,看上面的式子,分别用到了\(e[i].w,e[i].w*size[x]\),直接分别维护即可,至于线段树信息怎么更新,额....,好问题,你发现如果只考虑一棵子树内的贡献的话,你直接线段树合并即可,但是另一部分的答案就会变得很难统计,这个时候就不太能用这个线段树上的信息来计算了,所以这个时候我们就要考虑怎么再去维护那一部分的信息。
首先先上一个图,便于一会描述:
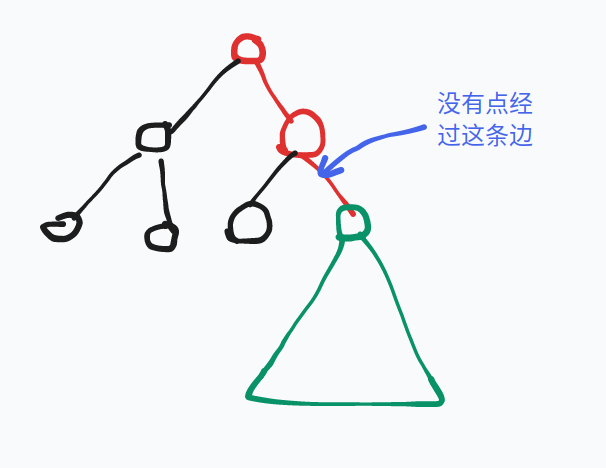
现在我们以箭头指向的那条边为界将树分为了两部分:绿色子树和(红+黑)的那棵树
首先绿色子树的贡献直接就可以线段树合并的时候计算,没啥要说的
主要还是红黑部分的贡献的计算:
首先这红黑两部分的\(size_{红黑}=totsize-size_{绿色子树}\)
先考虑红色这条链的贡献计算,可以发现红色这条链完全可以用一个以\(size\)为下标的权值树状数组,当你进入一个节点时加上它的贡献,离开时再减去就好,贡献的计算和上面一样,只不过它这条链上的每一个节点的\(size\)都减去了一个\(size_{绿色子树}\),查询时分界点稍微左偏一下即可
再考虑黑色部分的贡献,虽说它的\(size\)并没有发生改变,但你发现它根本没法用任何东西维护,这个时候就可以直接统计全局对于\(size_{红黑}\)的贡献,然后直接减去绿色子树和红色链上对于\(size_{红黑}\)的贡献就好了,这两个东西都是可以\(O(log)\)做的,至于全局贡献直接开个前缀和数组记一下就好了,直接\(O(1)\)解决了
然后就没啥了,哦,记得离散化一下\(size\)再拿来做下标,要不然可能有点卡常,最后贴个代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define ls lc[rt]
#define rs rc[rt]
#define pii pair<int,int>
#define fi first
#define se second
#define met(x) memset(x,0,sizeof x)
const int N=1e6+5;
int n,m,a[N],ans[N],sum1[N],sum2[N],w[N];
int x,y,z,l,r,k,t,sum,res,len,root[N];
int h[N],tot,b[N],size[N],wp[N],h1,h2;
struct sb{
int nxt,to,w;
}e[N];
inline void add(int x,int y,int z){
e[++tot]={h[x],y,z};
h[x]=tot;
}
inline int read(){
int s=0;char c=getchar_unlocked();
while(c<'0'||c>'9')c=getchar_unlocked();
while(c>='0'&&c<='9'){s=(s<<1)+(s<<3)+(c^48);c=getchar_unlocked();}
return s;
}
inline void dfs(int x,int fa){
size[x]=a[x];
for(int i=h[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==fa)continue;
dfs(y,x);
w[y]=e[i].w;
size[x]+=size[y];
}
b[x]=size[x];
// cout<<x<<" "<<b[x]<<endl;
}
struct tree{
int tot,w1[N<<2],w2[N<<2],lc[N<<2],rc[N<<2];
inline void clear(){tot=0;met(w1);met(w2);met(lc);met(rc);}
inline void tag(int rt,int v1,int v2){w1[rt]+=v1,w2[rt]+=v2;}
inline void pushup(int rt){w1[rt]=w1[ls]+w1[rs];w2[rt]=w2[ls]+w2[rs];}
inline void add(pii &a,pii b){a.fi+=b.fi;a.se+=b.se;}
inline void add(int &rt,int l,int r,int pos,int v1,int v2){
if(!rt)rt=++tot;
if(l==r)return tag(rt,v1,v2);
int mid=(l+r)>>1;
pos<=mid?add(ls,l,mid,pos,v1,v2):add(rs,mid+1,r,pos,v1,v2);
pushup(rt);
}
inline pii query(int rt,int l,int r,int L,int R){
if(!rt)return {0,0};
if(L<=l&&r<=R)return {w1[rt],w2[rt]};
int mid=(l+r)>>1;pii res={0,0};
if(L<=mid)add(res,query(ls,l,mid,L,R));
if(R>mid)add(res,query(rs,mid+1,r,L,R));
return res;
}
inline int merge(int x,int y){
if(!x||!y)return x^y;
w1[x]+=w1[y];w2[x]+=w2[y];
lc[x]=merge(lc[x],lc[y]);
rc[x]=merge(rc[x],rc[y]);
return x;
}
}T1;
struct shu{
//支持单点修改,前缀查询
int c1[N],c2[N];
inline int lb(int x){return x&-x;}
inline void clear(){for(int i=1;i<=n;i++)c1[i]=c2[i]=0;}
inline void add(int x,int w1,int w2){while(x<=len)c1[x]+=w1,c2[x]+=w2,x+=lb(x);}
inline pii ask(int x){pii res={0,0};while(x){res.fi+=c1[x],res.se+=c2[x],x-=lb(x);}return res;}
}T2;
//ans=size[x]*e[i].w(size[x]<=totsize/2)+(totsize-size[x])*e[i].w(size[x]>totsize/2)
//ans=size[x]*e[i].w(<=) -size[x]*e[i].w(>) +totsize*((size[x]>totsize/2)*e[i].w)
//开一个下标为size的值域线段树存储两个信息 e[i].w e[i].w*size[x]
inline void get_ans(int x,int fa,int w){
T1.add(root[x],1,len,wp[x],w,size[x]*w);
T2.add(wp[x],w,size[x]*w);ans[x]=0;
h1+=w;h2+=size[x]*w;
for(int i=h[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==fa)continue;
get_ans(y,x,e[i].w);
//子树内
pii res=T1.query(root[y],1,len,upper_bound(b+1,b+1+len,size[y]/2)-b,len);
ans[y]+=res.fi*size[y]-res.se//size>size[y]/2的贡献
+T1.w2[root[y]]-res.se;//size<size[y]/2的贡献
//链上
int sz=size[1]-size[y];
int pos=upper_bound(b+1,b+1+len,sz/2+size[y])-b;
res=T2.ask(pos-1);
ans[y]+=res.se-res.fi*size[y]+(h1-res.fi)*size[y]+(h1-res.fi)*sz-(h2-res.se);
//全局贡献(对于size==size[1]-size[y])(一会再减去算重的贡献)
pos=upper_bound(b+1,b+1+len,sz/2)-b;
ans[y]+=sum2[pos-1]//size<sz/2的贡献
+sz*(sum1[len]-sum1[pos-1])-(sum2[len]-sum2[pos-1]);//size>sz/2的贡献
//减去子树里重复的贡献
res=T1.query(root[y],1,len,pos,len);
ans[y]-=res.fi*sz-res.se//size>size[y]/2的贡献
+T1.w2[root[y]]-res.se;//size<size[y]/2的贡献
//减去链上重复的贡献
res=T2.ask(pos-1);
ans[y]-=res.se+(h1-res.fi)*sz-(h2-res.se);
T1.merge(root[x],root[y]);
}
T2.add(wp[x],-w,-size[x]*w);
h1-=w;h2-=size[x]*w;
}
signed main(){
freopen("banking.in","r",stdin);
freopen("banking.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
t=read();
while(t--){
n=read();tot=0;
T1.clear();T2.clear();
for(int i=1;i<=n;i++)root[i]=h[i]=0;
for(int i=1;i<=n;i++)a[i]=read();
for(int i=1;i<n;i++){
x=read(),y=read(),z=read();
add(x,y,z);add(y,x,z);
}
dfs(1,0);
sort(b+1,b+1+n);
len=unique(b+1,b+1+n)-b-1;
for(int i=1;i<=n;i++)sum1[i]=sum2[i]=0;
for(int i=1;i<=n;i++){
wp[i]=lower_bound(b+1,b+1+len,size[i])-b;
sum1[wp[i]]+=w[i];sum2[wp[i]]+=w[i]*size[i];
}
for(int i=1;i<=len;i++)sum1[i]+=sum1[i-1],sum2[i]+=sum2[i-1];
get_ans(1,0,0);
int ANS=1e18;
for(int i=2;i<=n;i++)ANS=min(ANS,ans[i]);
cout<<ANS<<'\n';
}
return 0;
}
T3 NOIP2024加赛2 T4灯笼 luoguP9312
抽象dp
还是先说一下\(O(n^4)\)的暴力,但感觉和正解没啥关系,就过一下就行了
设\(dp_{l,r,s}\)表示能照明高度\(l-r\),并且能走到\(s\),转移比较冗杂,考虑的限制多并且重复状态也多,感觉没啥前途
而且我们发现在暴力的过程中我们是以每一个灯笼为起点向外扩展到\(1-n\),一共做了\(n\)遍,这样我们不如直接从\(1-n\),向里直接扩展到每个单点的贡献,这样只需要做一遍即可,直接上正解吧
设\(dp_{u,v}\)表示以\(u\)号灯为照明高度下界,\(v\)号灯为照明高度上界,对于一个新灯笼,要想取它做贡献当且仅当当前状态的照明区间与新灯笼照明区间有交,即
这个转移是\(O(n^3)\)的,发现还是无法通过,但是你又发现这个东西只要你以\(l\)从小到大排序,\(r\)从大到小排序保证两边边界的单调性,对于每个上下边界开一个优先队列来存最优状态,并每次转移\(pop\)不合法状态(此时不合法,以后也不会合法),就可以做到\(O(n^2logn)\)
还是贴个代码吧:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define cs top().first
#define po top().second
#define mp make_pair
const int N=2e3+5;
int n,k;
int dp[N][N],h[N];//dp[u][v]表示以u的下界为下界,v的上界为上界的最小代价
int pos[N],a[N],b[N],w[N];//位置,高度上限/下限,花费代价
int odera[N],oderb[N];//按a,b大小决定便利顺序
int up[N][2],dw[N][2];//提前预处理出对于每座山峰上的灯能延伸到的所有山峰的边界
bool cmpa(int x,int y){return a[x]<a[y];}
bool cmpb(int x,int y){return b[x]>b[y];}
priority_queue<pair<int,int>>ql[N],qr[N];
//ql[u]用来记录以u为区间最左端的最小值,qr[v]用来记录以v为区间最右段的最小值
signed main(){
freopen("lantern.in","r",stdin);
freopen("lantern.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>h[i];
for(int i=1;i<=k;i++)cin>>pos[i]>>w[i]>>a[i]>>b[i];
for(int i=1;i<=k;i++)odera[i]=oderb[i]=i;
sort(odera+1,odera+1+k,cmpa);
sort(oderb+1,oderb+1+k,cmpb);
for(int i=1;i<=k;i++){
for(up[i][0]=pos[i];up[i][0]>=1&&h[up[i][0]]<=b[i];up[i][0]--);
for(up[i][1]=pos[i];up[i][1]<=n&&h[up[i][1]]<=b[i];up[i][1]++);
for(dw[i][0]=pos[i];dw[i][0]>=1&&h[dw[i][0]]>=a[i];dw[i][0]--);
for(dw[i][1]=pos[i];dw[i][1]<=n&&h[dw[i][1]]>=a[i];dw[i][1]++);
}
for(int i=1;i<=k;i++)for(int j=1;j<=k;j++){
int u=odera[i],v=oderb[j];
dp[u][v]=1e10;
int l=max(dw[u][0],up[v][0]),r=min(dw[u][1],up[v][1]);
if(pos[u]<=l||pos[u]>=r||pos[v]<=l||pos[v]>=r||(a[u]>a[v]&&b[u]>b[v]))continue;//除去不合法状态
if(a[u]==1&&b[v]==n)dp[u][v]=0;
else if(a[u]>a[v])dp[u][v]=dp[v][v];
else if(b[u]>b[v])dp[u][v]=dp[u][u];
else{
while(!ql[u].empty()&&(pos[ql[u].po]<=l||pos[ql[u].po]>=r||a[ql[u].po]>b[v]||b[ql[u].po]<a[u]))ql[u].pop();
if(!ql[u].empty())dp[u][v]=min(dp[u][v],-ql[u].cs);
while(!qr[v].empty()&&(pos[qr[v].po]<=l||pos[qr[v].po]>=r||a[qr[v].po]>b[v]||b[qr[v].po]<a[u]))qr[v].pop();
if(!qr[v].empty())dp[u][v]=min(dp[u][v],-qr[v].cs);
}
if(dp[u][v]!=1e10)ql[u].push(mp(-dp[u][v]-w[v],v)),qr[v].push(mp(-dp[u][v]-w[u],u));
}
for(int i=1;i<=k;i++)cout<<(dp[i][i]==1e10?-1:dp[i][i]+w[i])<<'\n';
return 0;
}
T4 多校A层冲刺NOIP2024模拟赛19 T2 两棵树
本来没想着写这道题题解的,但一想到自己以后可能忘了,还是提一嘴吧:
首先你要知道一件事:对于一个森林,\(连通块的数量=点的数量-边的数量\),知道这个之后,此题就可以将贡献拆成四部分:
1.\(numdian_{a}*numdian_{b}\)
观察到对于每一个点\(x\),除了它本身,它可以和其他任意一个点产生期望贡献,即为$ \frac{1}{2}* \frac{1}{2}(两个点均未被删除)$
则总期望贡献为\(n*(n-1)* \frac{1}{4}\)
2.\(numdian*numbian\)
这个虽然有两项,但贡献相同,直接一起讨论了
观察到对于每一条边\(xy\),除了\(x,y\),它可以和其他任意一个点\(u\)产生期望贡献,即为$ \frac{1}{2}* \frac{1}{2} *\frac{1}{2}(三个点均未被删除)$
则总期望贡献为\((n-1)*(n-2)* \frac{1}{8}*2\)
3.\(numbian*numbian\)
还是和上面一样,对于两条边\(xy,uv\)要保证\(x!=y!=u!=v\)并且如果计算一个树内点\(x,y\),那在另一棵树内就不能统计所有带\(x,y\),的边(一棵树内选了\(x,y\),另一棵树内就肯定没有\(x,y\)),如果\(x,y\)之间有边,直接减度数的话可能会多减一个\(1\),最后加上就好
代码就很显然了:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=3e5+5,p=998244353;
int n,m,d[N],k,t;
int x,y,z,l,r,ans;
vector<int>v[N];
unordered_map<int,int>mp[N];
int inv2=499122177,inv16=935854081;
signed main(){
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n;
ans=(n-1)*inv2%p;
for(int i=1;i<n;i++){
cin>>x>>y;
d[x]++;d[y]++;
if(x>y)swap(x,y);
mp[x][y]=1;
}
for(int i=1;i<n;i++){
cin>>x>>y;
if(x>y)swap(x,y);
int vis=mp[x][y];
ans=(ans+(n-1-d[x]-d[y]+vis)*inv16%p)%p;
}
cout<<ans<<endl;
return 0;
}
T5 多校A层冲刺NOIP2024模拟赛19 T4 编辑
原QOJ5312
弱化版 luogu P5479 [BJOI2015] 隐身术
编辑距离,我去抽象东西,讲正解之前我还是想先说一下正常\(O(n^3)\)求编辑距离,事实上也没啥
对于两个字符串\(s_{1},s_{2}\),设\(f_{i,j}\)表示\(s_{1}\)匹配到\(i\),\(s_{2}\)匹配到\(j\)的最短距离
则有转移:
初值的话就是\(f[i][0]=i,f[0][i]=i\)
这个东西无论空间还是时间都是\(O(n^2)\)的,放在这题肯定不行,但其他题感觉就很实用,主要是简单易懂啊~~
不扯别的了,说一下这题正解
观察到k值事实上是非常小的,考虑更改状态设计,设\(f_{i,j}\)表示编辑距离小于等于\(i\),匹配上的字符串\(|s|-|t|=j\),最大能延伸到的位置为\(f_{i,j}\),因为\(-k≤j≤k\),所以状态数最多只会有\(k^2\)个转移直接效仿求编辑距离的转移就好,本质和上面还是一样的。感觉这题只是状态比较难想而已
没了,代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define ull unsigned long long
const int N=1e5+5,bs=237;
int n,m,k;
int x,y,z,l,r,ans[N];
string s,t;
int f[35][101];
//f[i][j]表示编辑距离小于等于i,匹配上的字符串|s|-|t|=j,最大能延伸到的位置为f[i][j]
//因为j<=k,所以状态数最多只会有k^2个转移直接效仿求编辑距离的转移就好
ull hss[N],hst[N],a[N];
inline ull get_hashs(int l,int r){return hss[r]-hss[l-1]*a[r-l+1];}
inline ull get_hasht(int l,int r){return hst[r]-hst[l-1]*a[r-l+1];}
inline bool check(int x,int y,int len){return get_hashs(x,x+len-1)==get_hasht(y,y+len-1);}
inline int LCP(int x,int y){
int l=1,r=min(n-x+1,m-y+1),res=0;
while(l<=r){
int mid=(l+r)>>1;
if(check(x,y,mid))l=mid+1,res=mid;
else r=mid-1;
}return res;
}
signed main(){
freopen("edit.in","r",stdin);
freopen("edit.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>k;
cin>>s>>t;
n=s.size();m=t.size();
s=' '+s;t=' '+t;a[0]=1;
for(int i=1;i<=max(n,m);i++)a[i]=a[i-1]*bs;
for(int i=1;i<=n;i++)hss[i]=hss[i-1]*bs+s[i];
for(int i=1;i<=m;i++)hst[i]=hst[i-1]*bs+t[i];
for(int st=1;st<=m;st++){
for(int i=0;i<=k;i++)for(int j=-i;j<=i;j++)f[i][j+k]=0;
f[0][k]=0;
for(int i=0;i<=k;i++){
for(int j=-i;j<=i;j++){
f[i][j+k]+=LCP(f[i][j+k]+1,st+f[i][j+k]+j);
if(i!=k){
f[i+1][j+k-1]=max(f[i+1][j+k-1],min(n,f[i][j+k]+1));
f[i+1][j+k]=max(f[i+1][j+k],min(f[i][j+k]+1,n));
f[i+1][j+k+1]=max(f[i+1][j+k+1],f[i][j+k]);
}
}
}
for(int j=-k;j<=k;j++){
if(j+n<=0||j+n>m-st+1)continue;
for(int i=0;i<=k;i++){
if(f[i][j+k]==n){ans[i]++;break;}
}
}
}
for(int i=0;i<=k;i++)cout<<ans[i]<<"\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号