山海经(线段树)

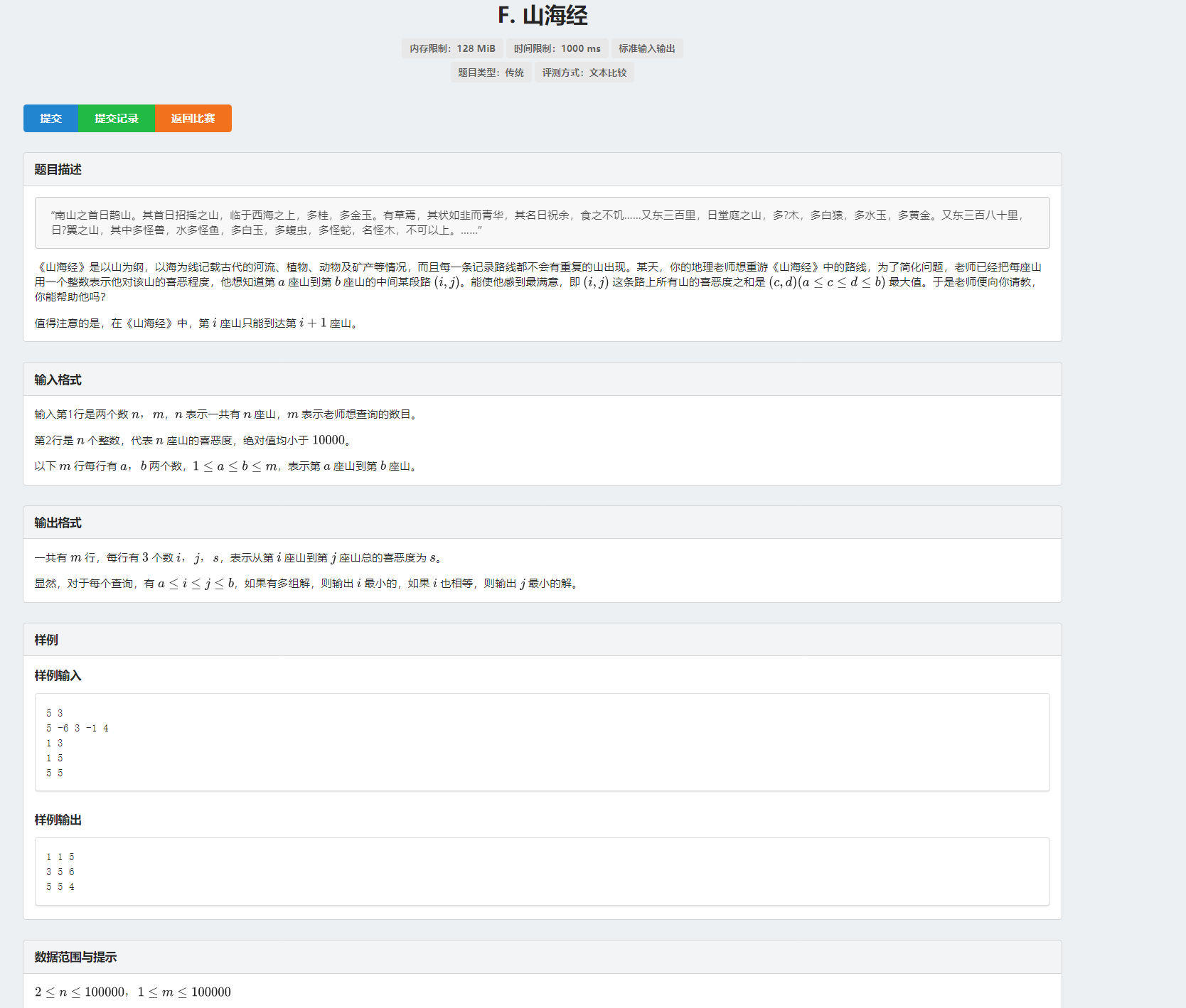
解：一眼看到这题，觉得是道板子题，但是如果直接暴力的话会kuku超时。所以只能智取！！
解释都在代码里，自行观看：

点击查看代码

#include<bits/stdc++.h>
#define ls rt<<1
#define rs rt<<1|1
#define mid ((tr[rt].l+tr[rt].r)>>1)
using namespace std;
const int N=4e7+10;
int n,m,w[N],o,p;
struct trr{
    int l,r,mmax,lmax,rmax;// 左端点，右端点，总最大值，左区间最大值，右区间最大值 
	int jll,jlr,zb,yb,sum;//所选区间左，右坐标，最大前缀和的右端点，最大后缀和的左端点 ，区间和 
}tr[N];
trr gengxin(trr a,trr b){//用两个儿子区间去更新父亲区间 
	trr now;//用一个结构体存父亲节点的值 
//  !!!!!!!!!!!!!!!!注意更新最大子段和的端点时要注意最左端的优先
	now.mmax=now.rmax=now.lmax=-0x3f3f3f3f;//求最大，赋极小 
    now.l=a.l;now.r=b.r;now.sum=a.sum+b.sum;
//	--------------------------------------------------------------------------------
//    合并时，区间最大子段和：左区间最大子段和、右区间最大子段和、左区间最大后缀和的max 
    if(now.mmax<a.mmax||(now.mmax==a.mmax&&now.jll>a.jll)){
    	now.mmax=a.mmax;
    	now.jll=a.jll;
    	now.jlr=a.jlr;
	}
	if(now.mmax<b.mmax||(now.mmax==b.mmax&&now.jll>b.jll)){
		now.mmax=b.mmax;
		now.jll=b.jll;
		now.jlr=b.jlr;
	}
	if(now.mmax<a.rmax+b.lmax||(now.mmax==a.rmax+b.lmax&&now.jll>a.yb)){
		now.mmax=a.rmax+b.lmax;
        now.jll=a.yb;
        now.jlr=b.zb;
	}
//	--------------------------------------------------------------------------------
//  区间最大前缀和：左区间最大前缀和、左区间和+右区间最大前缀和
	now.lmax=a.lmax;now.zb=a.zb;
	if(a.sum+b.lmax>now.lmax){
		now.lmax=a.sum+b.lmax;
		now.zb=b.zb;
	} 
//	--------------------------------------------------------------------------------
//	区间最大后缀和：右区间最大后缀和、左区间最大后缀和+右区间和
	now.rmax=b.rmax;now.yb=b.yb;
	if(a.rmax+b.sum>=now.rmax){
		now.rmax=a.rmax+b.sum;
		now.yb=a.yb; 
	}
	return now;
}
void build(int rt,int l,int r){//递归建树 ，同时更新父节点 
	tr[rt].l=l;tr[rt].r=r;
	if(l==r){
		tr[rt].mmax=tr[rt].lmax=tr[rt].rmax=tr[rt].sum=w[l];
		tr[rt].jll=tr[rt].jlr=tr[rt].zb=tr[rt].yb=l;
		return;
	}
	int m=mid;
	build(ls,l,m);
	build(rs,m+1,r);
	tr[rt]=gengxin(tr[ls],tr[rs]);
} 
trr chu(int rt,int l,int r){//递归查找范围最大值 
	if(tr[rt].l>=l&&tr[rt].r<=r)return tr[rt];
	int m=mid;
	if(l>m)return chu(rs,l,r);
	else if(r<=m)return chu(ls,l,r);
	else return gengxin(chu(ls,l,r),chu(rs,l,r)); 
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d",&w[i]);
	} 
	build(1,1,n);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&o,&p);
		trr now=chu(1,o,p);
		printf("%d %d %d\n",now.jll,now.jlr,now.mmax);
	}
	return 0;
}