数据结构——第五章查找:01静态查找表和动态查找表
1.查找表可分为两类:
(1)静态查找表:仅做查询和检索操作的查找表。
(2)动态查找表:在查询之后,还需要将查询结果为不在查找表中的数据元素插入到查找表中;或者,从查找表中删除其查询结果为在查找表中的数据元素。
2.查找的方法取决于查找表的结构:由于查找表中的数据元素之间不存在明显的组织规律,因此不便于查找。为了提高查找效率,需要在查找表中的元素之间人为地附加某种确定的关系,用另外一种结构来表示查找表。
3.顺序查找表:以顺序表或线性链表表示静态查找表,假设数组0号单元留空。算法如下:
int location(SqList L, ElemType &elem)
{
i = 1;
p = L.elem;
while (i <= L.length && *(p++)!= e)
{
i++;
}
if (i <= L.length)
{
return i;
} else
{
return 0;
}
}
此算法每次循环都要判断数组下标是否越界,改进方法:加入哨兵,将目标值赋给数组下标为0的元素,并从后向前查找。改进后算法如下:
int Search_Seq(SSTable ST, KeyType kval) //在顺序表ST中顺序查找其关键字等于key的数据元素。若找到,则函数值为该元素在表中的位置,否则为0。
{
ST.elem[0].key = kval; //设置哨兵
for (i = ST.length; ST.elem[i].key != kval; i--) //从后往前找,找不到则返回0
{
}
return 0;
}
4.顺序表查找的平均查找长度为:(n+1)/2。
5.上述顺序查找表的查找算法简单,但平均查找长度较大,不适用于表长较大的查找表。若以有序表表示静态查找表,则查找过程可以基于折半进行。算法如下:
int Search_Bin(SSTable ST, KeyType kval)
{
low = 1;
high = ST.length; //置区间初值
while (low <= high)
{
mid = (low + high) / 2;
if (kval == ST.elem[mid].key)
{
return mid; //找到待查元素
} else if (kval < ST.elem[mid].key)
{
high = mid - 1; //继续在前半区间查找
} else
{
low = mid + 1; //继续在后半区间查找
}
}
return 0; //顺序表中不存在待查元素
} //表长为n的折半查找的判定树的深度和含有n个结点的完全二叉树的深度相同
6.几种查找表的时间复杂度:
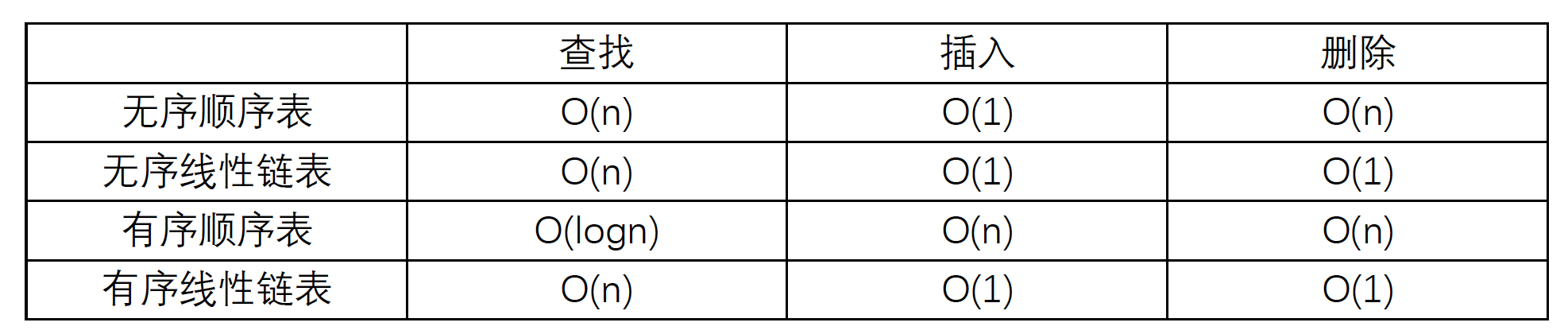
(1)从查找性能看,最好情况能达到O(logn),此时要求表有序;
(2)从插入和删除性能看,最好情况能达到O(1),此时要求存储结构是链表。
7.二叉排序树(二叉查找树):
(1)定义:二叉排序树或者是一棵空树;或者是具有如下特性的二叉树:
①若它的左子树不空,则左子树上所有结点的值均小于根结点的值;
②若它的右子树不空,则右子树上所有的结点值均大于根结点的值;
③它的左、右子树也都分别是二叉排序树(对二叉排序顺进行中序遍历得到的是一个有序序列)。
(2)通常取二叉链表作为二叉排序树的存储结构。
typedef struct BiTNode //结点结构
{
TElemType data;
struct BiTNode* lchild, *rchild; //左右孩子指针
} BiTNode, *BiTree;
(3)二叉排序树的查找算法:若二叉排序树为空,则查找不成功;否则:
①若给定值等于根结点的关键字,则查找成功;
②若给定值小于根结点的关键字,则继续在左子树上进行查找;
③若给定值大于根结点的关键字,则继续在右子树上进行查找。
(4)从上述查找过程可见,在查找过程中,生成了一条查找路径:
①查找成功:从根结点出发,沿着左分支或右分支逐层向下直至关键字等于给定值的结点;
②查找不成功:从根结点出发,沿着左分支或右分支逐层向下直至指针指向空树为止。
(5)二叉排序树中递归地查找关键字算法:
Status SearchBST(BiTree T, KeyType kval, BiTree f, BiTree &p) //在根指针T所指二叉排序树中递归地查找其关键字等于kval的数据元素,若查找成功,则返回指针p指向该数据元素的结点,并返回函数值为TRUE;否则表明查找不成功,返回FALSE,指针f指向当前访问结点的双亲,其初始调用值为NULL(f用于二叉排序树的插入操作)
{
if (!T)
{
p = f;
return FALSE; //查找不成功
} else if (kval == T->data.key)
{
p = T;
return TRUE;
} else if (kval < T->data.key)
{
return SearchBST(T->lchild, kval, T, p); //在左子树中继续查找
} else
{
return SearchBST(T->rchild, kval, T, p); //在右子树中继续查找
}
}
(6)二叉排序树的插入算法:根据动态查找表的定义,插入操作在查找不成功时才进行;若二叉排序树为空树,则新插入的结点为新的根结点;否则,新插入的结点必为一个新的叶子结点,其插入位置由查找过程得到。算法如下:
Status Insert BST(BiTree &T, ElemType e) //当二叉排序树中不存在关键字等于e.key的数据元素时,插入元素值为e的结点,并返回TRUE;否则,不进行插入并返回FALSE
{
if (!SearchBST(T, e.key, NULL, p))
{
s = new BiTNode; //为新结点分配空间
s->data = e;
s->lchild = s->rchild = NULL;
if (!p)
{
T = s; //插入s为新的根结点
} else if (e.key < p->data.key)
{
p->lchild = s; //插入*s为*p的左孩子
} else
{
p->rchild = s; //插入*s为*p的右孩子
}
return TRUE; //插入成功
} else
{
return FALSE;
}
}
(7)二叉排序树的删除算法:和插入相反,删除在查找成功之后进行,并且要求在删除二叉排序树上某个结点之后,仍然保持二叉排序树的特性。可分三种情况讨论:
①被删除的结点是叶子:其双亲结点中相应指针域的值改为空;
②被删除的结点只有左子树或者只有右子树:其双亲结点的相应指针域的值改为指向被删除结点的左子树或右子树;
③被删除的结点既有左子树,也有右子树:以其前驱结点替换该结点,再删除该前驱结点;或者以其后继节点替换该结点,再删除该后继结点。
算法描述如下:
Status DeleteBST(BiTree &T, KeyType kval) //若二叉排序树T中存在其关键字等于kval的数据元素,则删除该数据元素结点,并返回函数值TRUE,否则返回函数值FALSE
{
if (!T)
{
return FALSE; //不存在关键字等于kval的数据元素
} else
{
if (kval == T->data.key)
{
Delete(T);
return TRUE; //找到关键字等于key的数据元素
} else if (kval < T->data.key)
{
return DeleteBST(T->lchild, kval); //继续在左子树中进行查找
} else
{
return DeleteBST(T->rchild, kval); //继续在右子树中进行查找
}
}
}
void Delete(BiTree &p) //从二叉排序树中删除结点p,并重接它的左子树或右子树
{
if (!p->rchild)
{
p = p->lchild;
} else if (!p->lchild)
{
p = p->rchild;
} else
{
tmp = p->left;
while (tmp->right)
{
tmp = tmp->right;
}
p->data = tmp->data;
Delete(tmp);
}
}
(8)查找性能分析:对于每一棵特定的二叉排序树,均可按照平均查找长度的定义来求它ASL,由值相同的n个关键字构造所得的不同形态的各棵二叉排序树的平均查找长度的值不同,甚至可能差别很大。
8.平衡二叉树:平衡二叉树是二叉查找树的另一种形式,特点为树中每个结点的左、右子树深度之差的绝对值不大于1。
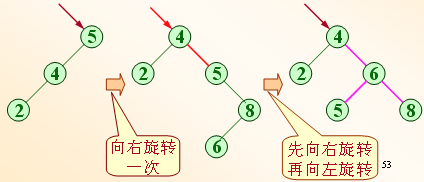
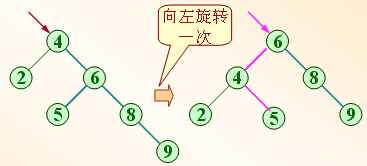
(1)构造平衡二叉(查找)树的方法是:在插入过程中,采用平衡旋转技术(LL、RR、LR、RL)。
(2)当发生不平衡的情况,找到最小不平衡子树进行调整:
①LL型:整体向右旋转一次;
②RR型:整体向左旋转一次;
③LR型:底部向左旋转一次,变成LL型,再整体向右旋转一次;
④RL型:底部向右旋转一次,变成RR型,再整体向左旋转一次。
例如:依次插入的关键字为5, 4, 2, 8, 6, 9
(3)平衡二叉树的查找性能分析:在平衡树上进行查找的过程和二叉排序树相同,因此查找过程中和给定值进行比较的关键字的个数不超过平衡树的深度。因此,在平衡二叉树上进行查找时,查找过程中和给定值进行比较的关键字的个数和log(n)相当(最坏情况等效于顺序表查找性能和n相当)。
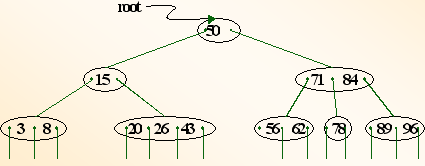
9.B树:
(1)定义:B树是一种平衡的多路查找树。在m阶的B树上,每个非终端结点可能含有:
①n个关键字Ki(1 ≤ i ≤ n,n < m);
②n个指向记录的指针Di(1 ≤ i ≤ n);
③n+1个指向子树的指针Ai(0 ≤ i ≤ n);
例如,下图为一棵B树:
(2)查找过程:
(3)插入操作:
(4)删除操作:
(5)查找性能分析:
10.B+树:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号