数据结构——第四章图：05拓扑排序和关键路径

1.拓扑排序问题提出：假设以有向图表示一个工程的施工图或程序的数据流图，则图中不允许出现回路（检查有向图中是否存在回路的方法之一，是对有向图进行拓扑排序）。

2.拓扑排序：对有向图进行如下操作：按照有向图给出的次序关系，将图中顶点排成一个线性序列，对于有向图中没有限定次序关系的顶点，则可以人为加上任意的次序关系。由此所得顶点的线性序列称之为拓扑有序序列。拓扑排序过程如下图所示：

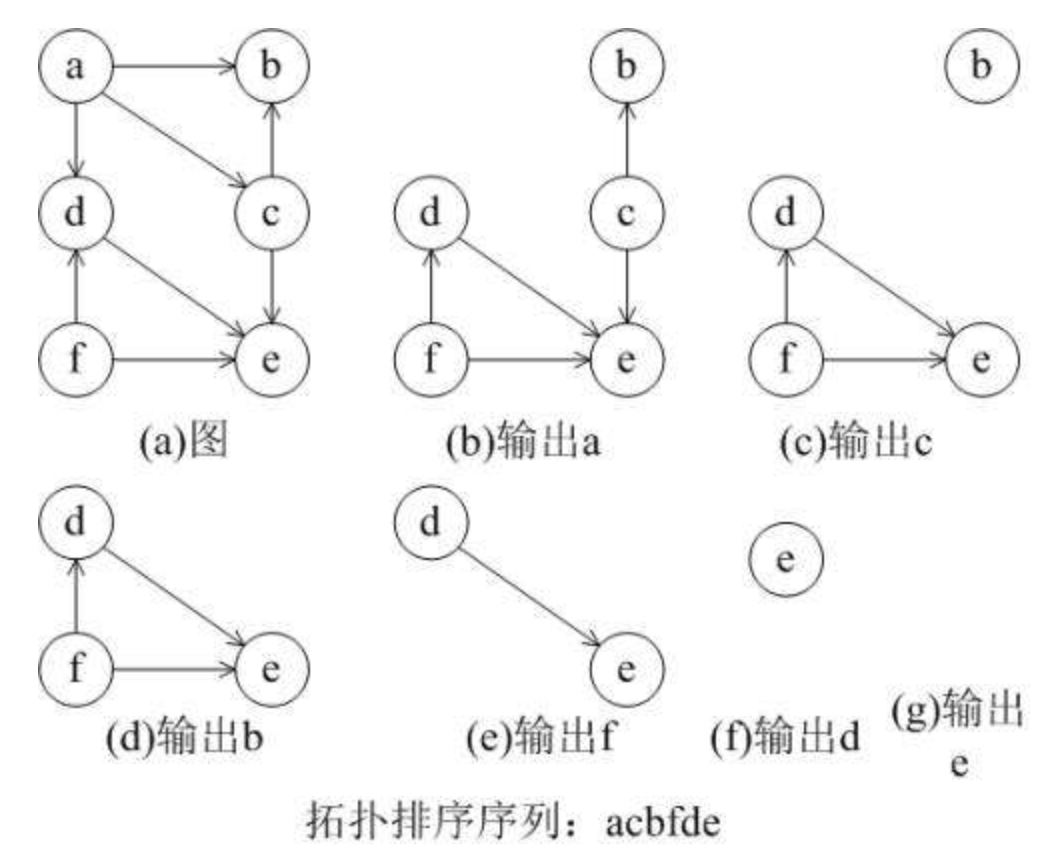
对于下列有向图，因为图中存在一个回路{B, C, D}，所以不能求得它的拓扑有序序列。

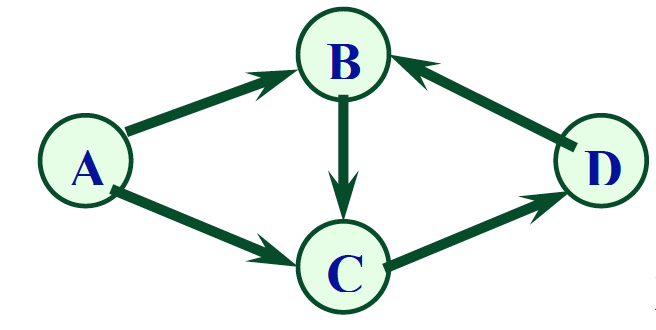
3.拓扑排序步骤：

（1）从有向图中选取一个没有前驱的顶点（入度为零的顶点），并输出。

（2）从有向图中删除此顶点以及所有以它为尾的弧；

重复上述两步，直至图空，或者图不空但找不到无前驱的顶点为止。

4.关键路径问题的提出：假设以有向网表示一个施工流图，弧上的权值表示完成该项子工程所需时间。影响整个工程完成期限的子工程项被称为关键工程。从起点到终点具有最大路径长度（该路径上的各个活动所持续的时间之和）的路径称为关键路径。

⑴ 只有在某顶点所代表的事件发生后，从该顶点出发的各活动才能开始；

⑵ 只有在进入某顶点的各活动都结束，该顶点所代表的事件才能发生。

5.整个工程完成的时间为：从有向图的源点到汇点的最长路径。关键活动指的是该弧上的权值增加使有向图上的最长路径的长度增加。

6.求关键活动方法：该活动的最早开始时间 = 该活动的最迟开始时间。

（1）事件（顶点）的最早发生时间ve(j) = 从源点到顶点j的最长路径长度；

（2）事件（顶点）的最迟发生时间vl(k) = 从顶点k到汇点的最短路径长度；

（3）活动（弧）的最早开始时间ee(i) = ve(j)；

（4）活动（弧）的最迟开始时间el(i) = vl(k) - dut(<j, k>); //dut为该弧权值 

7.事件发生时间的计算公式：

（1）ve(源点) = 0；ve(k) = Max{ve(j) + dut(<j, k>)}；

（2）vl(汇点) = ve(汇点)；vl(j) = Min{vl(k) - dut(<j, k>)};

例如下图求关键路径过程：

     

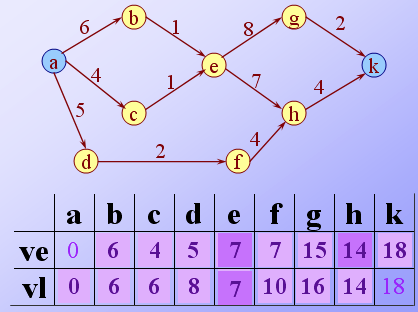
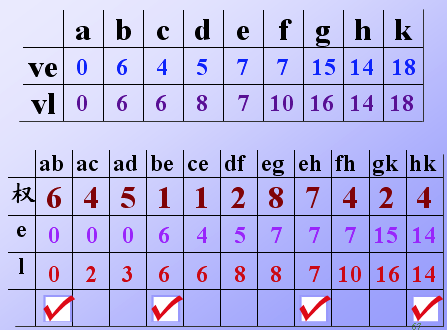
8.求ve的顺序是按拓扑有序次序，求vl的顺序是按拓扑逆序的次序。