数据结构——第四章图：04最小生成树

1.（连通网的）最小生成树问题提出：假设要在n个城市之间建立通讯联络网，则连通n个城市只需要修建n-1条线路，如果在最节省经费的前提下建立这个通讯网？该问题等价于：构造网的一棵最小生成树，即：在e条带权的边中选取n-1条边（不构成回路），使权值之和为最小。有两种算法：Prim（普利姆）算法和Kruskal（克鲁斯卡尔）算法。

2.Prim算法的基本思想（加点法）：取图中任意一个顶点v作为生成树的根，之后往生成树上添加新的顶点w。在添加的顶点w和已经在生成树上的顶点v之间必定存在一条边，并且该边的权值在所有连通顶点v和w之间的边中取值最小。之后继续往生成树上添加顶点，直至生成树上含有n个顶点为止。一般情况下所添加的顶点应满足下列条件：在生成树的构造过程中，图中n个顶点分属两个集合：已落在生成树上的顶点集U和尚未落在生成树上的顶点集V-U，则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边。例如下图最小生成树的生成过程：

     

3.Kruskal算法的基本思想（加边法）：

（1）考虑问题的出发点：为使生成树上边的权值之和达到最小，则应使生成树中每一条边的权值尽可能小。

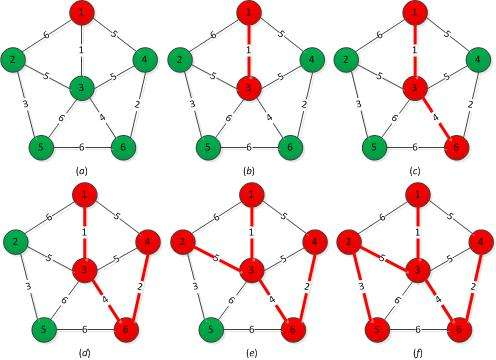
（2）具体做法：先构造一个只含n个顶点的子图SG，然后从权值最小的边开始，若它的添加不使SG中产生回路，则在SG上加上这条边，直至加上n-1条边为止。例如下图最小生成树的生成过程：

算法描述：

构造非连通图ST = (V, {});

k = i = 0; //k计选中的边数

while (k < n - 1)

{

　　i++;

　　检查边集E中第i条权值最小的边(u, v); 若(u, v)加入ST后不使ST中产生回路，则输出边(u, v); 且k++;

}

5.两种算法适用范围：普利姆算法适用于稠密图，克鲁斯卡尔算法适用于稀疏图。