数据结构——第三章树和二叉树：03树和森林

1.树的三种存储结构：

（1）双亲表示法：

#define MAX_TREE_SIZE 100

结点结构：

typedef struct PTNode

{

　　Elem data;

　　int parent; //双亲位置域

} PTNode;

（2）孩子双亲链表表示法：

 

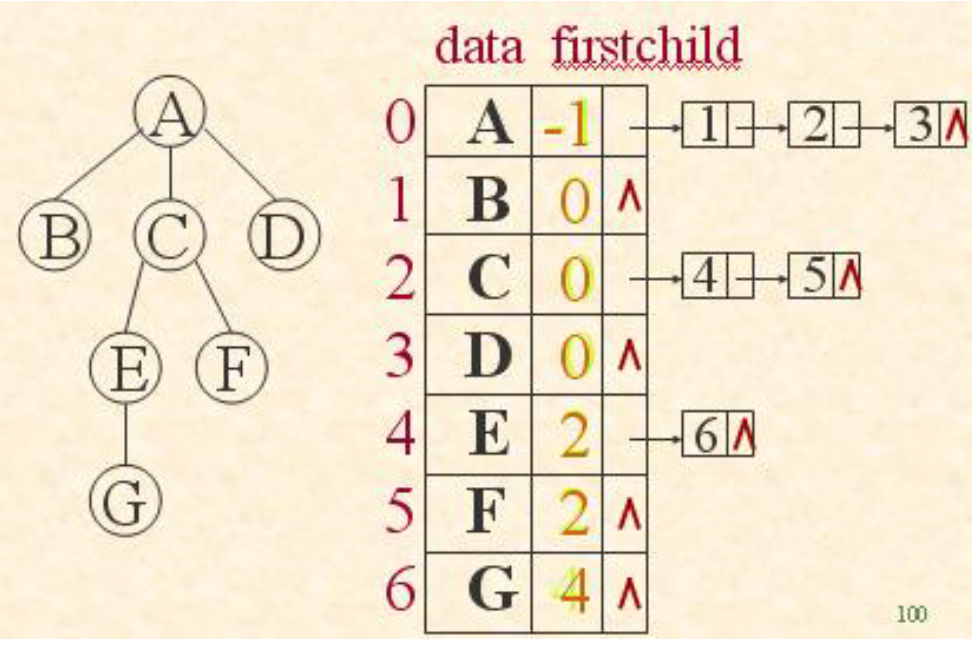
typedef struct PTNode

{

　　Elem data;

　　int parent; //双亲位置域

　　struct CTNode* nextchild;

} *ChildPtr;

（3）树的二叉链表（孩子-兄弟）存储表示法：

           

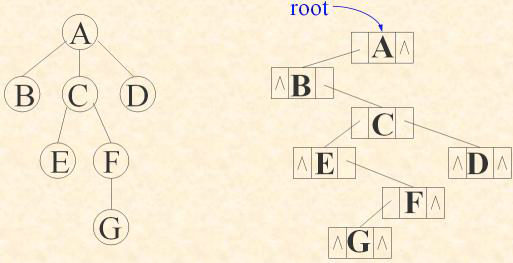
结点结构：

typedef struct CSNode

{

　　Elem data;

　　struct CSNode *firstchild, *nextsibling;

} CSNode, *CSTree;

2.森林和二叉树的对应关系：

设森林：F = (T₁, T₂, ... , T_n); T₁ = (root, t₁₁, t₁₂, ... , t_1m); 

二叉树：B = (LBT, Node(root), RBT);

（1）由森林转换成二叉树的转换规则为：若F = ∅，则B = ∅；否则，由ROOT(T₁)对应得到Node(root)；由(t₁₁, t₁₂, ... , t_1m)对应得到LBT；由(T₂, T₃, ... , T_n)对应得到RBT。

（2）由二叉树转换为森林的转换规则为：若B = ∅，则F = ∅；否则，由Node(root)对应得到ROOT(T₁)；由LBT对应得到（t₁₁,t₁₂, ... , t_1m）；由RBT对应得到（T₂, T₃, ... , T_n）。

（和树对应的二叉树，其左、右子树的概念，已改变为左是孩子，右是兄弟）

 3.树转换为二叉树：将一棵树转换为二叉树主要根据树的孩子-兄弟存储方式，方法是：

（1）树中所有相邻兄弟之间加一条连线；

（2）对树中的每个结点，只保留其与第一个孩子结点之间的连线，删去其与其它孩子结点之间的连线；

（3）以树的根结点为轴心，将整棵树顺时针旋转一定角度，使之结构层次分明 

 4.森林转换为二叉树：森林是若干棵树的集合。树可以转换为二叉树，森林同样也可以转换为二叉树。因此，森林也可以方便地使用孩子-兄弟链表表示。森林转换为二叉树的方法如下：

（1）将森林中的每棵树转换成相应的二叉树。

（2）第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子，当所有二叉树连在一起后，所得到的二叉树就是由森林转换得到的二叉树。

5.二叉树还原为树或森林：树和森林都可以转换为二叉树，二者的不同是：树转换成的二叉树，其根结点必然无右孩子，而森林转换后的二叉树，其根结点有右孩子。将一棵二叉树还原为树或森林，具体方法如下：

（1）若某结点是其双亲的左孩子，则把该结点的右孩子、右孩子的右孩子...都与该结点的双亲结点用先线连起来。

（2）删掉原二叉树中所有双亲结点与右孩子结点的连接。

（3）整理由前两步所得到的树或森林，使之结构层次分明。

 6.树的遍历：

（1）先根遍历：若树不空，则先访问根结点，然后依次先根遍历各棵子树。

（2）后根遍历：若树不空，则先依次后根遍历各棵子树，然后访问根结点。

（3）层次遍历：若树不空，则自上而下，自左至右访问树中每个结点。