数据结构——第三章树和二叉树:02二叉树
1.二叉树的存储结构:
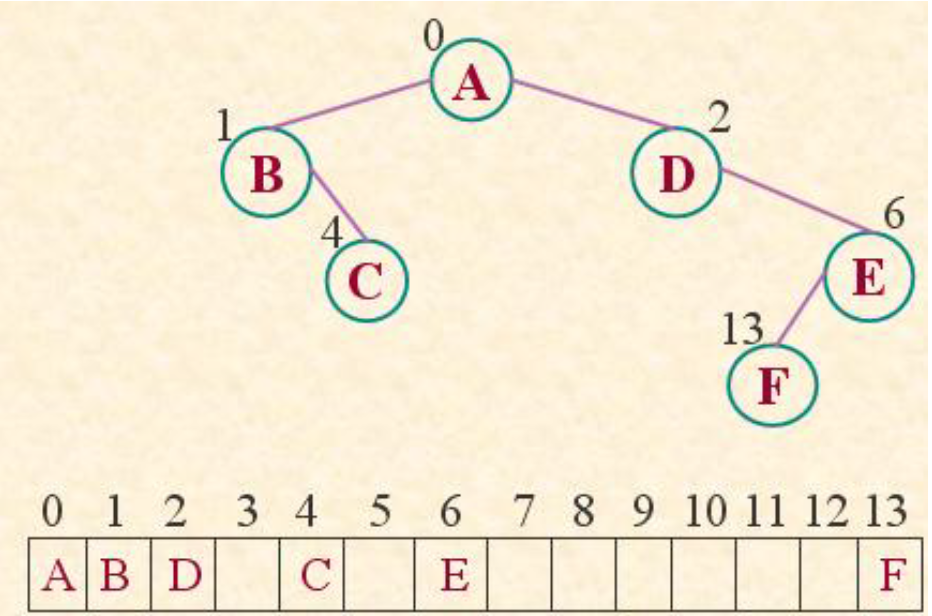
(1)二叉树的顺序存储表示:
#define MAX_TREE_SIZE 100 //二叉树的最大结点数
typedef TElemType SqBiTree[MAX_TREE_SIZE];
SqBiTree bt;
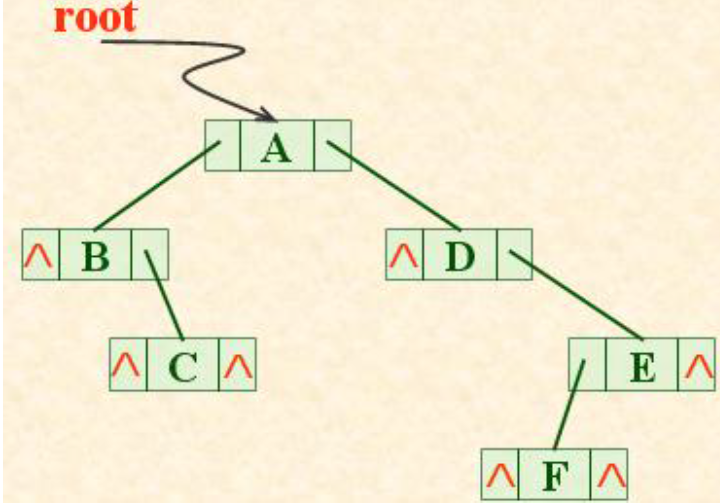
(2)二叉树的链式存储表示:
①二叉链表:
typedef struct BiTNode //结点结构
{
TElemType data;
struct BiTNode *lchild, *rchild; //左右孩子指针
} BiTNode, *BiTree;
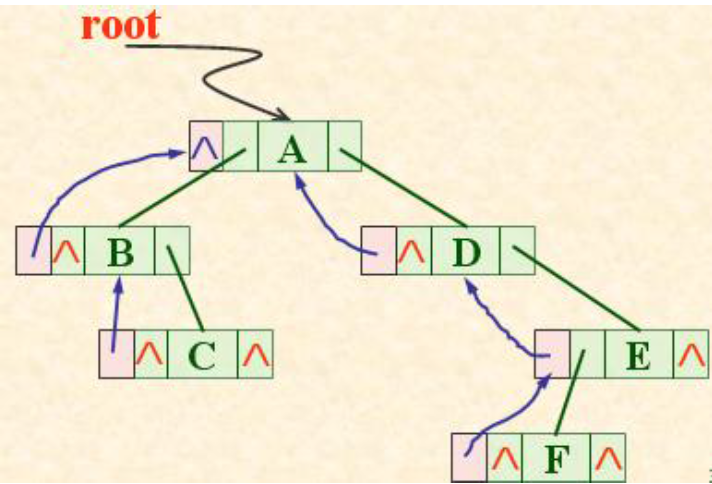
②三叉链表:如要找某个结点的父结点,在三叉链表中很容易实现,在二叉链表中则需从根指针出发一一查找。
typedef struct TriTNode //结点结构
{
TElemType data;
struct TriTNode *lchild, *rchild; //左右孩子指针
struct TriTNode *parent; //双亲指针
} TriTNode, *TriTree;
2.若一个二叉树中含有n个结点,则它的二叉链表中必含有2n个指针域,其中必有n + 1个空的链域。
证明:分支数目B = n - 1,即非空的链域有n - 1个,空链域有2n - (n - 1) = n + 1个。
3.二叉树的遍历:顺着某一条搜索路径巡防二叉树中的结点,使得每个结点均被访问一次,而且仅被访问一次。对于二叉树可以有三条搜索路径:先上后下的按层次遍历;先左(子树)后右(子树)的遍历;先右子树后左子树的遍历。
(1)先左后右的遍历算法:递归操作
①先根遍历:若二叉树为空树,则空操作;否则,访问根结点->先序遍历左子树->先序遍历右子树。
先根遍历的递归算法描述:
void Preorder(BiTree T)
{
if (T)
{
visit(T->data); //访问根结点
Preorder(T->lchild); //遍历左子树
Preorder(T->rchild); //遍历右子树
}
}
先根遍历的非递归算法描述:
②中根遍历:若二叉树为空树,则空操作;否则,中序遍历左子树->访问根结点->中序遍历右子树。
中根遍历的递归算法描述:
void Inorder(BiTree T)
{
if (T)
{
Inorder(T->lchild); //遍历左子树
visit(T->data); //访问根结点
Inorder(T->rchild); //遍历右子树
}
}
中根遍历的非递归算法描述:
void Inorder(BiTree T)
{
InitStack(&S);
p = T;
while (p != NULL || !StackEmpty(S))
{
if (p != NULL) //p指针不空则进栈,p指向p的左子树
{
push(&S, p);
p = p->lchild;
} else //p指针为空则出栈,p指向p的右子树
{
pop(&S, p);
visit(p->data);
p = p->rchild;
}
}
}
③后根遍历:若二叉树为空树,则空操作;否则,后序遍历左子树->后序遍历右子树->访问根结点。
后根遍历的递归算法描述:
void Postorder(BiTree T)
{
if (T)
{
Postorder(T->lchild); //遍历左子树
Postorder(T->rchild); //遍历右子树
visit(T->data); //访问根结点
}
}
后根遍历的非递归算法描述:
4.根据先序遍历和中序遍历、中序遍历和后序遍历可以确定一棵二叉树,而根据先序遍历和后序遍历不能唯一确定一棵二叉树(原因是通过中序遍历可以划分出左右子树,先序遍历的根在左边,后序遍历的根在右边,无法划分出左右子树)。
5.统计二叉树中叶子结点个数(函数之间进行数据传递的三种方式):
(1)方法一:通过函数参数传递
void CountLeaf(BiTree T, int* count)
{
if (T)
{
if ((!T->lchild) && (!T->rchild))
{
(*count)++; //叶子结点计数加1
}
CountLeaf(T->lchild, count);
CountLeaf(T->rchild, count);
}
}
(2)方法二:通过全局变量传递
int count = 0;
void CountLeaf(BiTree T)
{
if (T)
{
CountLeaf(T->lchild);
CountLeaf(T->rchild);
if ((!T->lchild) && (!T->rchild))
{
count++;
}
}
}
(3)方法三:通过返回值传递
int CountLeaf(BiTree T)
{
if (!T)
{
return 0;
}
if (!T->lchild && !T->rchild)
{
return 1;
} else
{
leftCount = CountLeaf(T->lchild);
rightCount = CountLeaf(T->rchild);
return m + n;
}
}
6.求二叉树的深度(后序遍历):从二叉树深度的定义可知,二叉树的深度应为其左、右子树深度的最大值加1。由此,需先分别求得左、右子树的深度,算法中访问结点的操作为:求得左、右子树深度的最大值,然后加1。
int Depth(BiTree T) //返回二叉树的深度
{
if (!T)
{
return 0;
} else
{
leftDepth = Depth(T->lchild);
rightDepth = Depth(T->rchild);
depth = 1 + (leftDepth > rightDepth) ? leftDepth : rightDepth;
}
return depth;
}
7.按层次遍历二叉树:
void levelOrder(BiTree T)
{
InitQueue(Q); //建立工作队列
EnQueue(Q, T); //将根结点入队
while (!QueueEmpty(Q)) //队列不空则继续循环
{
DeQueue(Q, p); //将队列首元素出队
visit(p); //访问出队元素
if (p->lchild) //如果出队元素左子树不空,则将左子树入队
{
EnQueue(Q, p->lchild);
}
if (p->rchild) //如果出队元素右子树不空,则将右子树入队
{
EnQueue(Q, p->rchild);
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号