10种经典统计方法总结
| 方法 | 适用问题 | 模型特点 | 模型类型 | 学习策略 | 学习的损失函数 | 学习算法 | 注意事项 | ||||||||||||
| 感知机 | 二类分类 | 分离超平面 |
判别模型
|
极小化误分点到超平面距离 |
误分点到超平面的距离
|
随机梯度下降 |
对偶解法(Gram矩阵) |
||||||||||||
| k近邻法 |
多类分类, 回归 |
特征空间, 样本点 |
判别模型
|
三要素: 1、距离度量:曼哈顿和欧氏距离 2、k值选取:(估计误差和近似误差),交叉验证求最优 3、分类决策:多数表决 kd树(构造和搜索,适用于训练实例远大于空间维数) |
|||||||||||||||
| 朴素贝叶斯法 | 多类分类 |
特征与类别的联合概率布,条件独立解释 |
生成模型
(学习联合概率,求条件概率) |
极大似然估计(参数估计), 极大后验概率估计 |
对数似然损失 |
概率计算公式, EM算法 |
(0-1损失函数)期望风险最小化就是后验概率最大化 概率估计:极大似然估计或贝叶斯估计(拉普拉斯平滑) |
||||||||||||
| 决策树 |
多类分类, 回归 |
分类树,回归树 |
判别模型
|
正则化的极大似然估计 | 对数似然损失 |
特征选择,生成, 剪枝 |
if-then规则:互斥并且完备 启发式学习,得出次最优 生成:局部最优;剪枝:全局最优
|
||||||||||||
|
逻辑斯蒂回归 和最大熵模型 |
多类分类 |
特征条件下类别的条件 概率分布,对数线性模型 |
判别模型 |
极大似然估计, 正则化的极大似然估计 |
逻辑斯蒂损失 二项:
|
改进的迭代尺度算法, 梯度下降, 拟牛顿法 |
还差最大熵模型 | ||||||||||||
| 支持向量机 | 二类分类 | 分离超平面,核技巧 |
判别模型 线性: 非线性(核):
|
极小化正则化合页函数 软间隔最大化 |
合页损失 | 序列最小最优化SMO算法(解决大样本下以往算法效率低的问题) |
凸优化问题是指约束最优化问题,最大分离间隔可化为凸二次规划问题 学习的对偶算法:拉格朗日对偶性 KKT条件:对偶问题和原始问题同最优化解 软间隔就是允许异常值的间隔 感知机的损失函数的右平移是合页函数 常用核:多项式核,高斯核 SMO:启发式算法,第一个变量a1是违反KKT最严重的样本点, 第二个变量a2是使其变化足够大的点 |
||||||||||||
| 提升方法 | 二类分类 | 弱分类器的线性组合 |
判别模型
|
极小化加法模型的指数损失 | 指数损失 | 前向分步加法算法 |
AdaBoost: 系数am:误差越大的分类器,权值am越小 系数wm: 误分类的样本的权值wm 加大,正确分类的wm减少 GBDT: 回归树:平方损失(残差),指数损失,梯度提升(针对一般的损失函数)
|
||||||||||||
| EM算法 | 概率模型参数估计 | 含隐变量概率模型 |
极大似然估计 极大后验概率估计 |
对数似然损失 | 迭代算法 |
不同初值可能得到不同的参数估计 EM算法是不断求下界的极大化逼近求解对数似然函数极大化的算法,不能保证收敛到全局最优 高斯混合模型的EM算法 E步:Q函数-完全数据的期望 M步:极大化Q函数
|
|||||||||||||
| 隐马尔可夫HMM | 标注 | 观测序列与状态序列的联合概率分布模型 |
生成模型 时序模型 |
极大似然估计 极大似然后验概率估计 |
对数似然损失 |
概率计算公式 EM算法 |
隐马尔可夫三要素λ=(A,B,∏) 两个假设:齐次马尔可夫和观测独立 概率计算:直接计算和前后向算法 学习问题(参数估计):监督学习法和非监督Baum-Welch算法(EM算法实现) 预测问题(求状态序列):近似算法和维特比算法(动态规划) |
||||||||||||
| 条件随机场CRF | 标注 | 状态序列条件下观测序列的条件概率分布,对数线性模型 | 判别模型 | 极大似然估计,正则化极大似然估计 | 对数似然损失 | 改进的迭代尺度算法,梯度下降,拟牛顿法 |


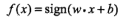

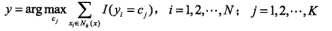
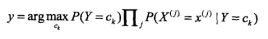
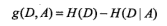
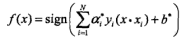
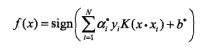
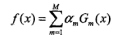
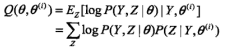

 浙公网安备 33010602011771号
浙公网安备 33010602011771号