ML面试1000题系列(51-60)
本文总结ML面试常见的问题集
转载来源:https://blog.csdn.net/v_july_v/article/details/78121924
51、简单说下sigmoid激活函数
常用的非线性激活函数有sigmoid、tanh、relu等等,前两者sigmoid/tanh比较常见于全连接层,后者relu常见于卷积层。这里先简要介绍下最基础的sigmoid函数(btw,在本博客中SVM那篇文章开头有提过)。
sigmoid的函数表达式如下
其中z是一个线性组合,比如z可以等于:b + 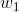
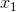
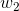
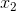
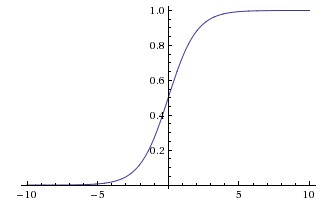
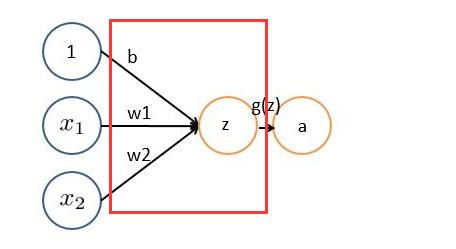
因此,sigmoid函数g(z)的图形表示如下( 横轴表示定义域z,纵轴表示值域g(z) ):
也就是说,sigmoid函数的功能是相当于把一个实数压缩至0到1之间。当z是非常大的正数时,g(z)会趋近于1,而z是非常小的负数时,则g(z)会趋近于0。
压缩至0到1有何用处呢?用处是这样一来便可以把激活函数看作一种“分类的概率”,比如激活函数的输出为0.9的话便可以解释为90%的概率为正样本。
举个例子,如下图(图引自Stanford机器学习公开课)
z = b + 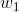
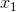
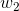
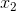
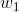
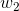
- 如果
= 0
= 0,则z = -30,g(z) = 1/( 1 + e^-z )趋近于0。此外,从上图sigmoid函数的图形上也可以看出,当z=-30的时候,g(z)的值趋近于0
- 如果
= 0
= 1,或
=1
= 0,则z = b +
*
+
*
= -30 + 20 = -10,同样,g(z)的值趋近于0
- 如果
= 1
= 1,则z = b +
*
+
*
= -30 + 20*1 + 20*1 = 10,此时,g(z)趋近于1。
换言之,只有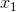
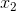
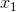
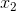
综上,sigmod函数,是逻辑斯蒂回归的压缩函数,它的性质是可以把分隔平面压缩到[0,1]区间一个数(向量),在线性分割平面值为0时候正好对应sigmod值为0.5,大于0对应sigmod值大于0.5、小于0对应sigmod值小于0.5;0.5可以作为分类的阀值;exp的形式最值求解时候比较方便,用相乘形式作为logistic损失函数,使得损失函数是凸函数;不足之处是sigmod函数在y趋于0或1时候有死区,控制不好在bp形式传递loss时候容易造成梯度弥撒。
什么是梯度弥散?当使用反向传播方法计算导数的时候,随着网络的深度的增加,反向传播的梯度(从输出层到网络的最初几层)的幅度值会急剧地减小。结果就造成了整体的损失函数相对于最初几层的权重的导数非常小。这样,当使用梯度下降法的时候,最初几层的权重变化非常缓慢,以至于它们不能够从样本中进行有效的学习。这种问题通常被称为“梯度的弥散”.
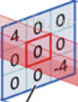
52、什么是卷积
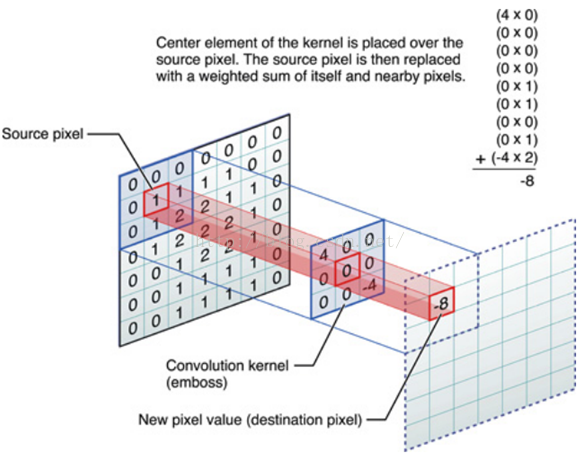
对应位置上是数字先相乘后相加
=
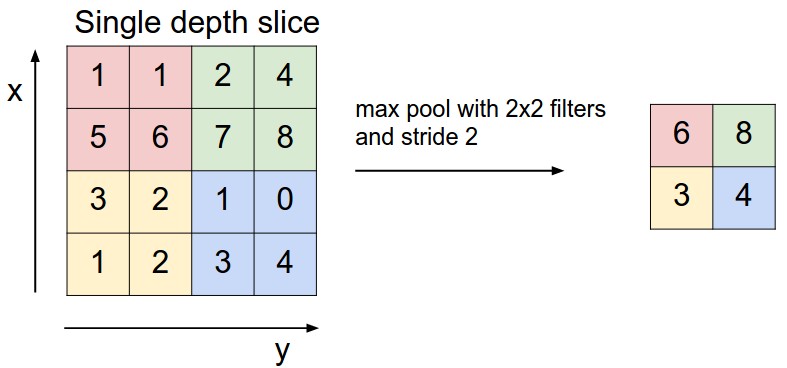
池化,简言之,即取区域平均或最大,如下图所示(图引自cs231n)
上图所展示的是取区域最大,即上图左边部分中 左上角2x2的矩阵中6最大,右上角2x2的矩阵中8最大,左下角2x2的矩阵中3最大,右下角2x2的矩阵中4最大,所以得到上图右边部分的结果:6 8 3 4。很简单不是?
54、 简述下什么是生成对抗网络。
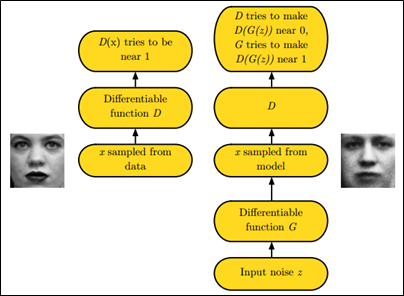
GAN之所以是对抗的,是因为GAN的内部是竞争关系,一方叫generator,它的主要工作是生成图片,并且尽量使得其看上去是来自于训练样本的。另一方是discriminator,其目标是判断输入图片是否属于真实训练样本。
更直白的讲,将generator想象成假币制造商,而discriminator是警察。generator目的是尽可能把假币造的跟真的一样,从而能够骗过discriminator,即生成样本并使它看上去好像来自于真实训练样本一样。

如下图中的左右两个场景:
55、学梵高作画的原理是啥?
解析参考:http://blog.csdn.net/lvonve/article/details/53320680
@LeftNotEasy,本题解析来源:http://www.cnblogs.com/LeftNotEasy/archive/2010/12/05/mathmatic_in_machine_learning_1_regression_and_gradient_descent.html下面是一个典型的机器学习的过程,首先给出一个输入数据,我们的算法会通过一系列的过程得到一个估计的函数,这个函数有能力对没有见过的新数据给出一个新的估计,也被称为构建一个模型。
我们用X1,X2..Xn 去描述feature里面的分量,比如x1=房间的面积,x2=房间的朝向等等,我们可以做出一个估计函数:
θ在这儿称为参数,在这儿的意思是调整feature中每个分量的影响力,就是到底是房屋的面积更重要还是房屋的地段更重要。为了如果我们令X0 = 1,就可以用向量的方式来表示了:
我们程序也需要一个机制去评估我们θ是否比较好,所以说需要对我们做出的h函数进行评估,一般这个进行评估的函数称为损失函数(loss function),描述h函数不好的程度,在下面,我们称这个函数为J函数
在这儿我们可以做出下面的一个损失函数:
换言之,我们把对x(i)的估计值与真实值y(i)差的平方和作为损失函数,前面乘上的1/2是为了在求导的时候,这个系数就不见了。
如何调整θ以使得J(θ)取得最小值有很多方法,其中有最小二乘法(min square),是一种完全是数学描述的方法,另外一种就是梯度下降法。
梯度下降法的算法流程如下:
1)首先对θ赋值,这个值可以是随机的,也可以让θ是一个全零的向量。
2)改变θ的值,使得J(θ)按梯度下降的方向进行减少。
为了描述的更清楚,给出下面的图:
 这是一个表示参数θ与误差函数J(θ)的关系图,红色的部分是表示J(θ)有着比较高的取值,我们需要的是,能够让J(θ)的值尽量的低,也就是达到深蓝色的部分。θ0,θ1表示θ向量的两个维度。
这是一个表示参数θ与误差函数J(θ)的关系图,红色的部分是表示J(θ)有着比较高的取值,我们需要的是,能够让J(θ)的值尽量的低,也就是达到深蓝色的部分。θ0,θ1表示θ向量的两个维度。
在上面提到梯度下降法的第一步是给θ给一个初值,假设随机给的初值是在图上的十字点。
然后我们将θ按照梯度下降的方向进行调整,就会使得J(θ)往更低的方向进行变化,如下图所示,算法的结束将是在θ下降到无法继续下降为止。
当然,可能梯度下降的最终点并非是全局最小点,即也可能是一个局部最小点,如下图所示:
上面这张图就是描述的一个局部最小点,这是我们重新选择了一个初始点得到的,看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点。
下面我将用一个例子描述一下梯度减少的过程,对于我们的函数J(θ)求偏导J:
下面是更新的过程,也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值,-后面的部分表示按梯度方向减少的量,α表示步长,也就是每次按照梯度减少的方向变化多少。
一个很重要的地方值得注意的是,梯度是有方向的,对于一个向量θ,每一维分量θi都可以求出一个梯度的方向,我们就可以找到一个整体的方向,在变化的时候,我们就朝着下降最多的方向进行变化就可以达到一个最小点,不管它是局部的还是全局的。
用更简单的数学语言进行描述步骤2)是这样的:
57、梯度下降法找到的一定是下降最快的方向么?
梯度下降法并不是下降最快的方向,它只是目标函数在当前的点的切平面(当然高维问题不能叫平面)上下降最快的方向。在practical implementation中,牛顿方向(考虑海森矩阵)才一般被认为是下降最快的方向,可以达到superlinear的收敛速度。梯度下降类的算法的收敛速度一般是linear甚至sublinear的(在某些带复杂约束的问题)。by林小溪(https://www.zhihu.com/question/30672734/answer/139689869)。
一般解释梯度下降,会用下山来举例。假设你现在在山顶处,必须抵达山脚下(也就是山谷最低处)的湖泊。但让人头疼的是,你的双眼被蒙上了无法辨别前进方向。换句话说,你不再能够一眼看出哪条路径是最快的下山路径,如下图(图片来源:http://blog.csdn.net/wemedia/details.html?id=45460):
最好的办法就是走一步算一步,先用脚向四周各个方向都迈出一步,试探一下周围的地势,用脚感觉下哪个方向是下降最大的方向。换言之,每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向(当前最陡峭的位置向下)走一步。就这样,每要走一步都根据上一步所在的位置选择当前最陡峭最快下山的方向走下一步,一步步走下去,一直走到我们感觉已经到了山脚。
当然这样走下去,我们走到的可能并不一定是真正的山脚,而只是走到了某一个局部的山峰低处。换句话说,梯度下降不一定能够找到全局的最优解,也有可能只是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。

@zbxzc(http://blog.csdn.net/u014568921/article/details/44856915):更进一步,我们来定义输出误差,即对于任意一组权值向量,那它得到的输出和我们预想的输出之间的误差值。定义误差的方法很多,不同的误差计算方法可以得到不同的权值更新法则,这里我们先用这样的定义:
上面公式中D代表了所有的输入实例,或者说是样本,d代表了一个样本实例,od表示感知器的输出,td代表我们预想的输出。
这样,我们的目标就明确了,就是想找到一组权值让这个误差的值最小,显然我们用误差对权值求导将是一个很好的选择,导数的意义是提供了一个方向,沿着这个方向改变权值,将会让总的误差变大,更形象的叫它为梯度。
既然梯度确定了E最陡峭的上升的方向,那么梯度下降的训练法则是:
梯度上升和梯度下降其实是一个思想,上式中权值更新的+号改为-号也就是梯度上升了。梯度上升用来求函数的最大值,梯度下降求最小值。
这样每次移动的方向确定了,但每次移动的距离却不知道。这个可以由步长(也称学习率)来确定,记为α。这样权值调整可表示为:
总之,梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以也被称为是“最速下降法”。最速下降法越接近目标值,步长越小,前进越慢。梯度下降法的搜索迭代示意图如下图所示:

正因为梯度度下降法在接近最优解的区域收敛速度明显变慢,所以利用梯度下降法求解需要很多次的迭代。在机器学习中,基于基本的梯度下降法发展了两种梯度下降方法,分别为随机梯度下降法和批量梯度下降法。by@wtq1993,http://blog.csdn.net/wtq1993/article/details/51607040
58、随机梯度下降
普通的梯度下降算法在更新回归系数时要遍历整个数据集,是一种批处理方法,这样训练数据特别忙庞大时,可能出现如下问题:
1)收敛过程可能非常慢;
2)如果误差曲面上有多个局极小值,那么不能保证这个过程会找到全局最小值。
为了解决上面的问题,实际中我们应用的是梯度下降的一种变体被称为随机梯度下降。
上面公式中的误差是针对于所有训练样本而得到的,而随机梯度下降的思想是根据每个单独的训练样本来更新权值,这样我们上面的梯度公式就变成了:
经过推导后,我们就可以得到最终的权值更新的公式:
有了上面权重的更新公式后,我们就可以通过输入大量的实例样本,来根据我们预期的结果不断地调整权值,从而最终得到一组权值使得我们的算法能够对一个新的样本输入得到正确的或无限接近的结果。
这里做一个对比
设代价函数为
批量梯度下降
参数更新为:
i是样本编号下标,j是样本维数下标,m为样例数目,n为特征数目。所以更新一个θj需要遍历整个样本集
随机梯度下降
参数更新为:
i是样本编号下标,j是样本维数下标,m为样例数目,n为特征数目。所以更新一个θj只需要一个样本就可以。
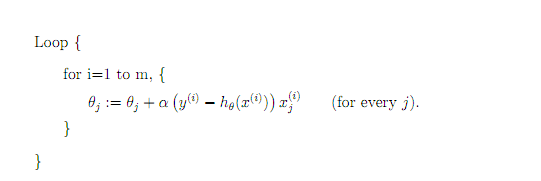
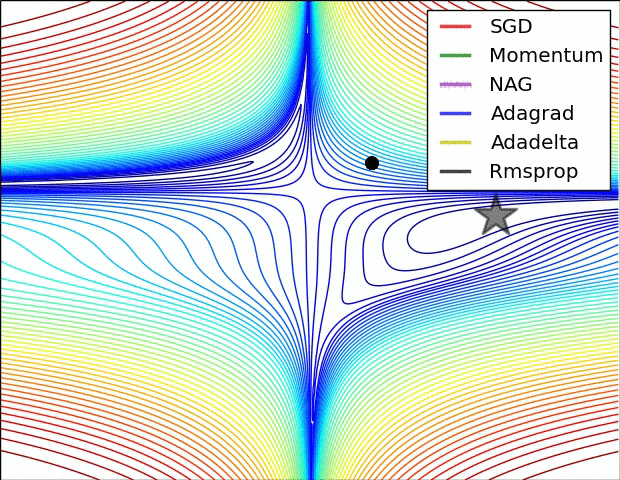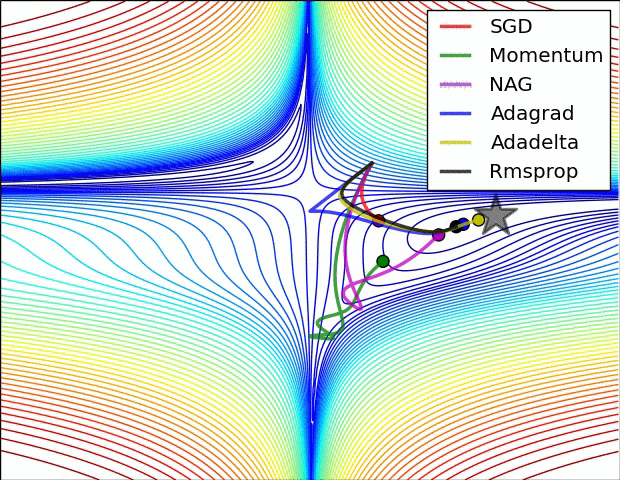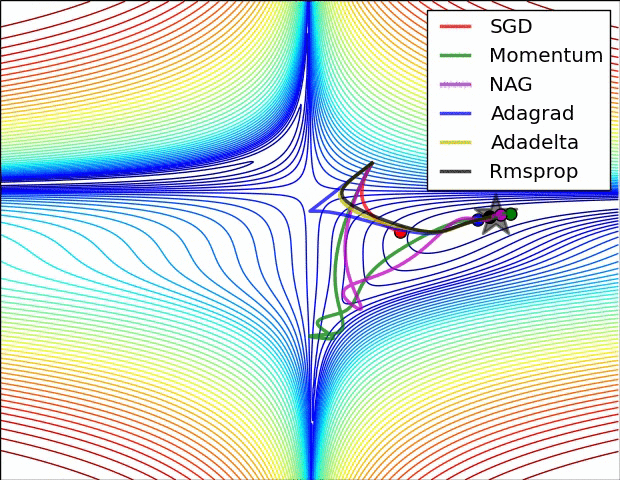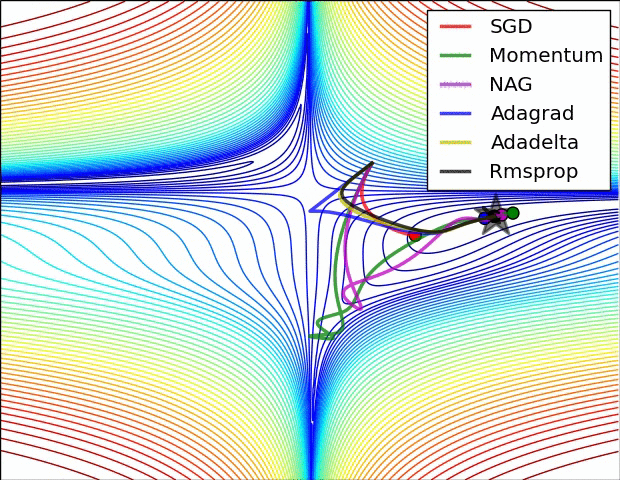
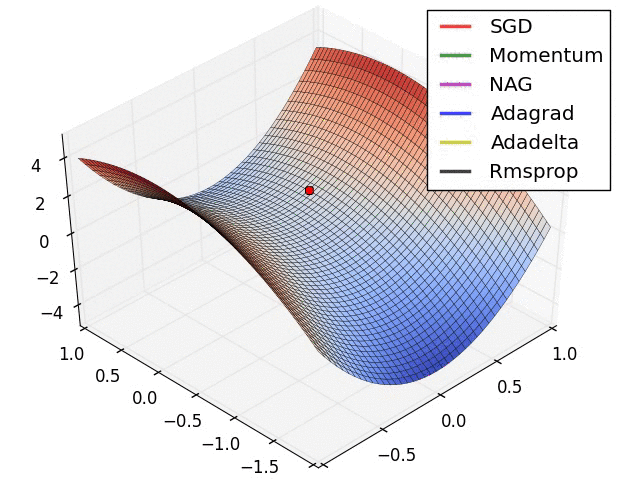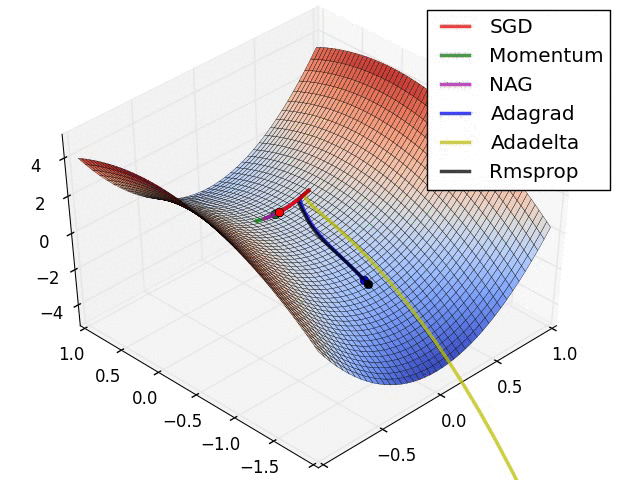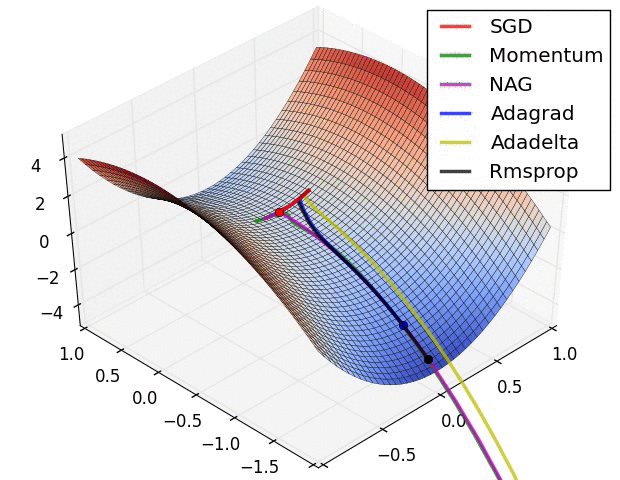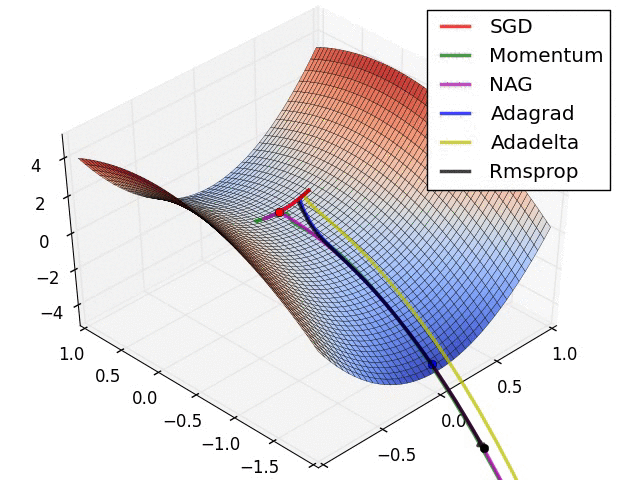
下面两幅图可以很形象的对比各种优化方法(图来源:http://sebastianruder.com/optimizing-gradient-descent/):
SGD各优化方法在损失曲面上的表现
从上图可以看出, Adagrad、Adadelta与RMSprop在损失曲面上能够立即转移到正确的移动方向上达到快速的收敛。而Momentum 与NAG会导致偏离(off-track)。同时NAG能够在偏离之后快速修正其路线,因为其根据梯度修正来提高响应性。
SGD各优化方法在损失曲面鞍点处上的表现
59、牛顿法和梯度下降法有什么不同
@wtq1993,http://blog.csdn.net/wtq1993/article/details/51607040
1)牛顿法(Newton's method)
牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。
具体步骤:
首先,选择一个接近函数 f (x)零点的 x0,计算相应的 f (x0) 和切线斜率f ' (x0)(这里f ' 表示函数 f 的导数)。然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和 x 轴的交点的x坐标,也就是求如下方程的解:

我们将新求得的点的 x 坐标命名为x1,通常x1会比x0更接近方程f (x) = 0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示:
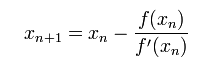
已经证明,如果f ' 是连续的,并且待求的零点x是孤立的,那么在零点x周围存在一个区域,只要初始值x0位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果f ' (x)不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
由于牛顿法是基于当前位置的切线来确定下一次的位置,所以牛顿法又被很形象地称为是"切线法"。牛顿法的搜索路径(二维情况)如下图所示:

关于牛顿法和梯度下降法的效率对比:
a)从收敛速度上看 ,牛顿法是二阶收敛,梯度下降是一阶收敛,前者牛顿法收敛速度更快。但牛顿法仍然是局部算法,只是在局部上看的更细致,梯度法仅考虑方向,牛顿法不但考虑了方向还兼顾了步子的大小,其对步长的估计使用的是二阶逼近。
b)根据wiki上的解释,从几何上说,牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。

注:红色的牛顿法的迭代路径,绿色的是梯度下降法的迭代路径。
牛顿法的优缺点总结:
优点:二阶收敛,收敛速度快;
缺点:牛顿法是一种迭代算法,每一步都需要求解目标函数的Hessian矩阵的逆矩阵,计算比较复杂。
什么是拟牛顿法(Quasi-Newton Methods)?
@wtq1993,http://blog.csdn.net/wtq1993/article/details/51607040
拟牛顿法是求解非线性优化问题最有效的方法之一,于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。Davidon设计的这种算法在当时看来是非线性优化领域最具创造性的发明之一。不久R. Fletcher和M. J. D. Powell证实了这种新的算法远比其他方法快速和可靠,使得非线性优化这门学科在一夜之间突飞猛进。
拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使用正定矩阵来近似Hessian矩阵的逆,从而简化了运算的复杂度。拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化,构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法,尤其对于困难的问题。另外,因为拟牛顿法不需要二阶导数的信息,所以有时比牛顿法更为有效。如今,优化软件中包含了大量的拟牛顿算法用来解决无约束,约束,和大规模的优化问题。
具体步骤:
拟牛顿法的基本思想如下。首先构造目标函数在当前迭代xk的二次模型:





60、请说说随机梯度下降法的问题和挑战?
那到底如何优化随机梯度法呢?详情请点击:论文公开课第一期:详解梯度下降等各类优化算法(含视频和PPT下载)。


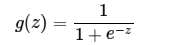

 对应位置上是数字先相乘后相加
对应位置上是数字先相乘后相加 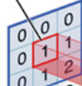 =
= 






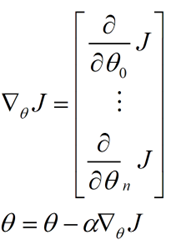
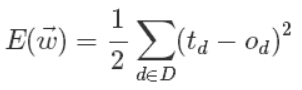
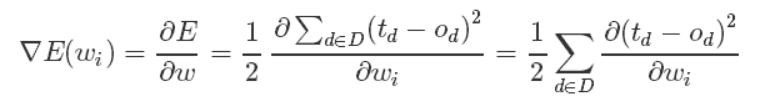

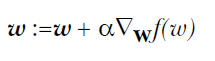
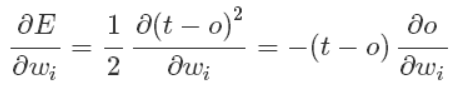
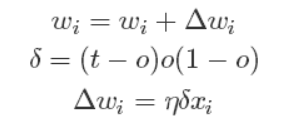
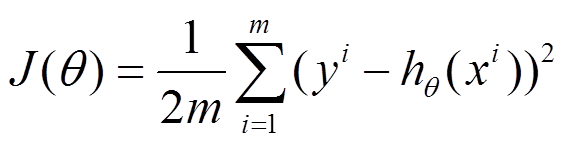
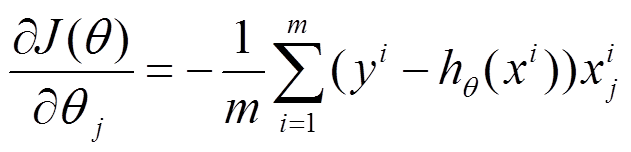
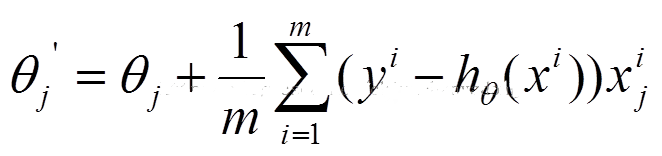
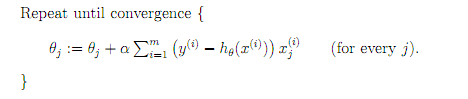
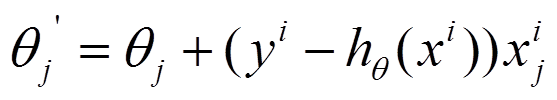





 浙公网安备 33010602011771号
浙公网安备 33010602011771号