ML面试1000题系列(31-40)
本文总结ML面试常见的问题集
转载来源:https://blog.csdn.net/v_july_v/article/details/78121924
31、下列哪个不属于CRF模型对于HMM和MEMM模型的优势(B )
A. 特征灵活 B. 速度快 C. 可容纳较多上下文信息 D. 全局最优
首先,CRF,HMM(隐马模型),MEMM(最大熵隐马模型)都常用来做序列标注的建模.
隐马模型一个最大的缺点就是由于其输出独立性假设,导致其不能考虑上下文的特征,限制了特征的选择
最大熵隐马模型则解决了隐马的问题,可以任意选择特征,但由于其在每一节点都要进行归一化,所以只能找到局部的最优值,同时也带来了标记偏见的问题,即凡是训练语料中未出现的情况全都忽略掉
条件随机场则很好的解决了这一问题,他并不在每一个节点进行归一化,而是所有特征进行全局归一化,因此可以求得全局的最优值。
此外《机器学习工程师第八期》里有讲概率图模型。
32、什么是熵
从名字上来看,熵给人一种很玄乎,不知道是啥的感觉。其实,熵的定义很简单,即用来表示随机变量的不确定性。
如果没有外部能量输入,封闭系统趋向越来越混乱(熵越来越大)。比如,如果房间无人打扫,不可能越来越干净(有序化),只可能越来越乱(无序化)。而要让一个系统变得更有序,必须有外部能量的输入。
更多请查看《最大熵模型中的数学推导》。
33、熵、联合熵、条件熵、相对熵、互信息的定义
- 大写字母X表示随机变量,小写字母x表示随机变量X的某个具体的取值;
- P(X)表示随机变量X的概率分布,P(X,Y)表示随机变量X、Y的联合概率分布,P(Y|X)表示已知随机变量X的情况下随机变量Y的条件概率分布;
- p(X = x)表示随机变量X取某个具体值的概率,简记为p(x);
- p(X = x, Y = y) 表示联合概率,简记为p(x,y),p(Y = y|X = x)表示条件概率,简记为p(y|x),且有:p(x,y) = p(x) * p(y|x)。
把最前面的负号放到最后,便成了:
上面两个熵的公式,无论用哪个都行,而且两者等价,一个意思(这两个公式在下文中都会用到)。
联合熵:两个随机变量X,Y的联合分布,可以形成联合熵Joint Entropy,用H(X,Y)表示。
条件熵:在随机变量X发生的前提下,随机变量Y发生所新带来的熵定义为Y的条件熵,用H(Y|X)表示,用来衡量在已知随机变量X的条件下随机变量Y的不确定性。
且有此式子成立:H(Y|X) = H(X,Y) – H(X),整个式子表示(X,Y)发生所包含的熵减去X单独发生包含的熵。至于怎么得来的请看推导:
简单解释下上面的推导过程。整个式子共6行,其中
- 第二行推到第三行的依据是边缘分布p(x)等于联合分布p(x,y)的和;
- 第三行推到第四行的依据是把公因子logp(x)乘进去,然后把x,y写在一起;
- 第四行推到第五行的依据是:因为两个sigma都有p(x,y),故提取公因子p(x,y)放到外边,然后把里边的-(log p(x,y) - log p(x))写成- log (p(x,y)/p(x) ) ;
- 第五行推到第六行的依据是:p(x,y) = p(x) * p(y|x),故p(x,y) / p(x) = p(y|x)。
相对熵:又称互熵,交叉熵,鉴别信息,Kullback熵,Kullback-Leible散度等。设p(x)、q(x)是X中取值的两个概率分布,则p对q的相对熵是:
在一定程度上,相对熵可以度量两个随机变量的“距离”,且有D(p||q) ≠D(q||p)。另外,值得一提的是,D(p||q)是必然大于等于0的。
互信息:两个随机变量X,Y的互信息定义为X,Y的联合分布和各自独立分布乘积的相对熵,用I(X,Y)表示:
且有I(X,Y)=D(P(X,Y) || P(X)P(Y))。下面,咱们来计算下H(Y)-I(X,Y)=H(Y| X)的结果,如下:
通过上面的计算过程,我们发现竟然有H(Y)-I(X,Y) = H(Y|X)。故通过条件熵的定义,有:H(Y|X) = H(X,Y) - H(X),而根据互信息定义展开得到H(Y|X) = H(Y) - I(X,Y),把前者跟后者结合起来,便有I(X,Y)= H(X) + H(Y) - H(X,Y),此结论被多数文献作为互信息的定义。更多请查看《最大熵模型中的数学推导》。
33、什么是最大熵
3.1 无偏原则
- 令x1表示“学习”被标为名词, x2表示“学习”被标为动词。
- 令y1表示“学习”被标为主语, y2表示被标为谓语, y3表示宾语, y4表示定语。
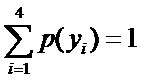 , 则根据无偏原则,认为这个分布中取各个值的概率是相等的,故得到:
, 则根据无偏原则,认为这个分布中取各个值的概率是相等的,故得到:因为没有任何的先验知识,所以这种判断是合理的。如果有了一定的先验知识呢?
因此,也就引出了最大熵模型的本质,它要解决的问题就是已知X,计算Y的概率,且尽可能让Y的概率最大(实践中,X可能是某单词的上下文信息,Y是该单词翻译成me,I,us、we的各自概率),从而根据已有信息,尽可能最准确的推测未知信息,这就是最大熵模型所要解决的问题。
相当于已知X,计算Y的最大可能的概率,转换成公式,便是要最大化下述式子H(Y|X):
且满足以下4个约束条件:
34、简单说下有监督学习和无监督学习的区别。
有监督学习:对具有标记的训练样本进行学习,以尽可能对训练样本集外的数据进行分类预测。(LR,SVM,BP,RF,GBDT)
无监督学习:对未标记的样本进行训练学习,比发现这些样本中的结构知识。(KMeans,DL)
35、了解正则化么。
正则化是针对过拟合而提出的,以为在求解模型最优的是一般优化最小的经验风险,现在在该经验风险上加入模型复杂度这一项(正则化项是模型参数向量的范数),并使用一个rate比率来权衡模型复杂度与以往经验风险的权重,如果模型复杂度越高,结构化的经验风险会越大,现在的目标就变为了结构经验风险的最优化,可以防止模型训练过度复杂,有效的降低过拟合的风险。
奥卡姆剃刀原理,能够很好的解释已知数据并且十分简单才是最好的模型。
36、协方差和相关性有什么区别?
相关性是协方差的标准化格式。协方差本身很难做比较。例如:如果我们计算工资($)和年龄(岁)的协方差,因为这两个变量有不同的度量,所以我们会得到不能做比较的不同的协方差。
为了解决这个问题,我们计算相关性来得到一个介于-1和1之间的值,就可以忽略它们各自不同的度量。
再来解释一波,比如X和Y的t1时刻的协方差为10000,在t2时刻的协方差为10,两个相比较差了100倍,因为两个协方差都是正数判断出X和Y都是同向变化,但看不出两者具有相似性。这是因为两者的变化幅度是不同的。为了准确判断相似度,重新定义相关系数。有点像SVM函数间隔和几何间隔的区别。
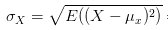
37、 线性分类器与非线性分类器的区别以及优劣。
@伟祺,线性和非线性是针对,模型参数和输入特征来讲的;比如输入x,模型y=ax+ax^2那么就是非线性模型,如果输入是x和X^2则模型是线性的。
线性分类器可解释性好,计算复杂度较低,不足之处是模型的拟合效果相对弱些。
非线性分类器效果拟合能力较强,不足之处是数据量不足容易过拟合、计算复杂度高、可解释性不好。
常见的线性分类器有:LR,贝叶斯分类,单层感知机、线性回归
常见的非线性分类器:决策树、RF、GBDT、多层感知机
SVM两种都有(看线性核还是高斯核)
38、数据的逻辑存储结构(如数组,队列,树等)对于软件开发具有十分重要的影响,试对你所了解的各种存储结构从运行速度、存储效率和适用场合等方面进行简要地分析。
| 运行速度 | 存储效率 | 适用场合 | ||
| 数组 | 快 | 高 | 比较适合进行查找操作,还有像类似于矩阵等的操作 | |
| 链表 | 较快 | 较高 | 比较适合增删改频繁操作,动态的分配内存 | |
| 队列 | 较快 | 较高 | 比较适合进行任务类等的调度 | |
| 栈 | 一般 | 较高 | 比较适合递归类程序的改写 | |
| 二叉树(树) | 较快 | 一般 | 一切具有层次关系的问题都可用树来描述 | |
| 图 | 一般 | 一般 | 除了像最小生成树、最短路径、拓扑排序等经典用途。还被用于像神经网络等人工智能领域等等。 |
39、什么是分布式数据库?
分布式数据库系统是在集中式数据库系统成熟技术的基础上发展起来的,但不是简单地把集中式数据库分散地实现,它具有自己的性质和特征。集中式数据库系统的许多概念和技术,如数据独立性、数据共享和减少冗余度、并发控制、完整性、安全性和恢复等在分布式数据库系统中都有了不同的、更加丰富的内容。
具体来说,集群文件系统是指运行在多台计算机之上,之间通过某种方式相互通信从而将集群内所有存储空间资源整合、虚拟化并对外提供文件访问服务的文件系统。其与NTFS、EXT等本地文件系统的目的不同,前者是为了扩展性,后者运行在单机环境,纯粹管理块和文件之间的映射以及文件属性。
集群文件系统分为多类,按照对存储空间的访问方式,可分为共享存储型集群文件系统和分布式集群文件系统,前者是多台计算机识别到同样的存储空间,并相互协调共同管理其上的文件,又被称为共享文件系统;后者则是每台计算机各自提供自己的存储空间,并各自协调管理所有计算机节点中的文件。Veritas的VxFS/VCS,昆腾Stornext,中科蓝鲸BWFS,EMC的MPFS,属于共享存储型集群文件系统。而HDFS、Gluster、Ceph、Swift等互联网常用的大规模集群文件系统无一例外都属于分布式集群文件系统。分布式集群文件系统可扩展性更强,目前已知最大可扩展至10K节点。
按照元数据的管理方式,可分为对称式集群文件系统和非对称式集群文件系统。前者每个节点的角色均等,共同管理文件元数据,节点间通过高速网络进行信息同步和互斥锁等操作,典型代表是Veritas的VCS。而非对称式集群文件系统中,有专门的一个或者多个节点负责管理元数据,其他节点需要频繁与元数据节点通信以获取最新的元数据比如目录列表文件属性等等,后者典型代表比如HDFS、GFS、BWFS、Stornext等。对于集群文件系统,其可以是分布式+对称式、分布式+非对称式、共享式+对称式、共享式+非对称式,两两任意组合。
按照文件访问方式来分类,集群文件系统可分为串行访问式和并行访问式,后者又被俗称为并行文件系统。
串行访问是指客户端只能从集群中的某个节点来访问集群内的文件资源,而并行访问则是指客户端可以直接从集群中任意一个或者多个节点同时收发数据,做到并行数据存取,加快速度。
HDFS、GFS、pNFS等集群文件系统,都支持并行访问,需要安装专用客户端,传统的NFS/CIFS客户端不支持并行访问。
40、 简单说说贝叶斯定理。
在引出贝叶斯定理之前,先学习几个定义:
- 条件概率(又称后验概率)就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
- 联合概率表示两个事件共同发生的概率。A与B的联合概率表示为
![]() 或者
或者![]() 。
。 - 边缘概率(又称先验概率)是某个事件发生的概率。边缘概率是这样得到的:在联合概率中,把最终结果中那些不需要的事件通过合并成它们的全概率,而消去它们(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率),这称为边缘化(marginalization),比如A的边缘概率表示为P(A),B的边缘概率表示为P(B)。
接着,考虑一个问题:P(A|B)是在B发生的情况下A发生的可能性。
- 首先,事件B发生之前,我们对事件A的发生有一个基本的概率判断,称为A的先验概率,用P(A)表示;
- 其次,事件B发生之后,我们对事件A的发生概率重新评估,称为A的后验概率,用P(A|B)表示;
- 类似的,事件A发生之前,我们对事件B的发生有一个基本的概率判断,称为B的先验概率,用P(B)表示;
- 同样,事件A发生之后,我们对事件B的发生概率重新评估,称为B的后验概率,用P(B|A)表示。
贝叶斯定理便是基于下述贝叶斯公式:
上述公式的推导其实非常简单,就是从条件概率推出。
所以,贝叶斯公式可以直接根据条件概率的定义直接推出。即因为P(A,B) = P(A)P(B|A) = P(B)P(A|B),所以P(A|B) = P(A)P(B|A) / P(B)。更多请参见此文:《从贝叶斯方法谈到贝叶斯网络》。


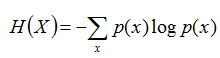
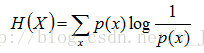
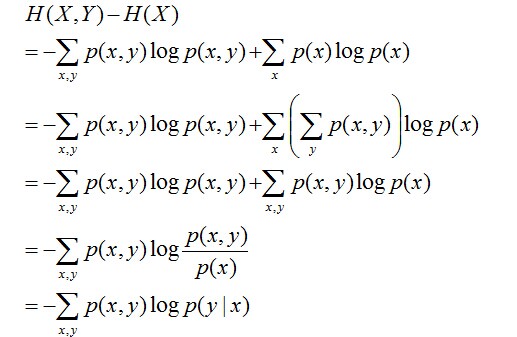
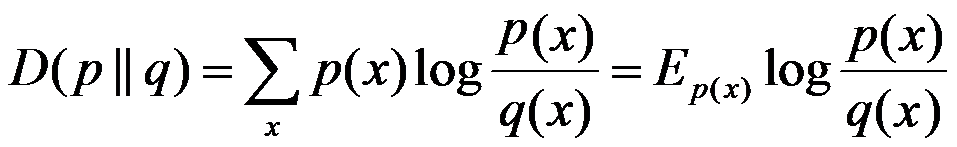
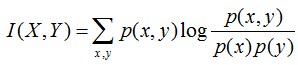
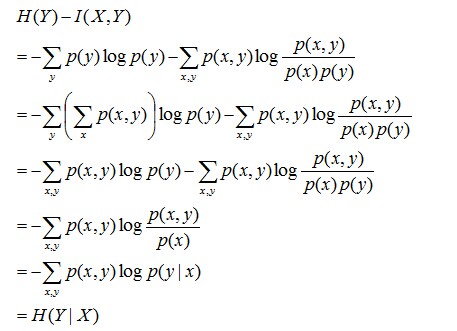
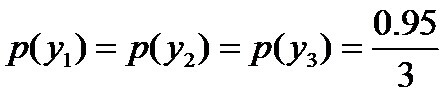
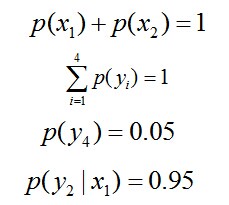
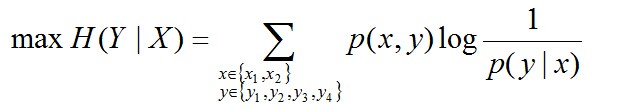
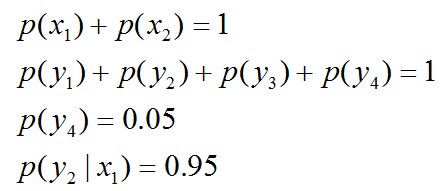
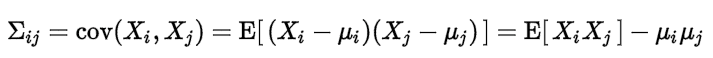
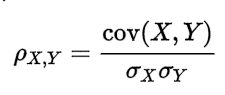
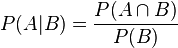
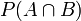 或者
或者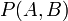 。
。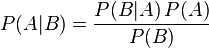
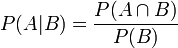
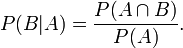
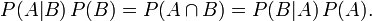
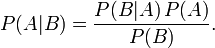

 浙公网安备 33010602011771号
浙公网安备 33010602011771号