计算机科学导论 笔记三（1） 【机械工业出版社-原书第二版】

第三章    数据存储

3.1数据类型

1. 5种不同的数据类型:数字,文字,音频,图像和视频  (计算机工业中使用术语"多媒体"来定义包含数字,文本,图像,音频和视频的信息.)

 

2.  位与位模式：

         位：一种通用格式，所有外部的数据类型都采用统一的数据表示法转换(0或1)后存入计算机，当数据从计算机输出时再还原回来，这种通用格式成为位。计算机使用各种各样的双态设备来存储数据。

         位模式：位模式是一个序列，有时也称位流（即0和1的序列）。通常长度为 8 的位模式被称为 1 个字节。

     属于不同数据类型的数据可以通过不同程序（数学公式，文本编辑器，图像记录仪，录音机，摄像机等）以同样的位模式存储在内存中。

     计算机内存存储所有这些而无需辨别它们表示的是何种数据类型。

 

3.2存储数字

---存储整数--定点表示法来存储整数，即，整数可以被当做小数点位置固定的数字，小数点固定在最右边（在这种表示法中，小数点是假定的，但并不存储）；无符号和有符号的整数在计算机中的存储方式是不同的。

    整数的存储：无符号表示法，符号加绝对值表示法，二进制补码表示法

1.无符号表示法：1）首先将整数变成二进制数，如果二进制位数不足 n 位，则左边补 0，使它的总位数为 n 位 。

                            例：将258存储在16位存储单元中：首先把258转化为二进制数，100000010，左边加 7 个 0 使总的位数满足 16 位的要求，即得到 0000000100000010 ，再将该整数被存储在存储单元中。

                 2）译解无符号整数：00101011，去掉左边两个0，容易算出十进制无符号整数为 43（2^5 + 2^3 + 2^1 + 1 = 43）。

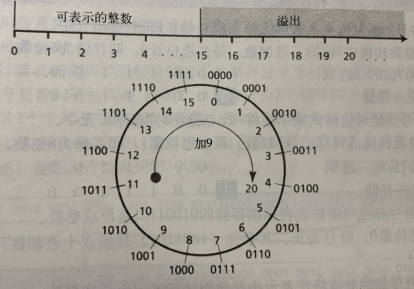
                 3）溢出：在 n 位存储单元中，我们可以存储的无符号整数仅为 0—2^n-1 之间。如图显示了假如存储大于 2^4-1=15 的整数仅为 4 位的内存中发出溢出的情况。

                             表示20的二进制数为10100，故计算机丢掉最左边的1，并保留右边的四位，变成 0100 。

                            

 

                4）无符号整数的应用：计数，寻址（有些计算机语言，在一个存储单元中存储了另一个存储单元的地址，地址都是从0 ，即存储器的第一个字节，开始到整个存储器的总字节数的正数），为其他数据类型排序（文本、图像、音频和视频是以位模式存储的，可以翻译为无符号整数）。

 

2.符号加绝对值表示法：1）该方法在存储整数时不常用，但该格式用于在计算机中存储部分实数。在这种方法中，用于无符号整数的有效范围被分为两个

 相等的子范围。前半个表示正整数，后半个表示负整数。列：。负数出现在正数的右边。且有+0和-0。

 

                  2）在图中容易看出，在 n 位单元可存储的数字范围是  -（2^n-1 -1）和  +（2^n-1 -1），且 n 位单元中最左边用于存储符号，0表示正，1表示负。例：用符号加绝对值表示法将 +28 存储在8位存储单元中---先将28变为二进制数11100，补到 7 位，即0011100，然后加符号存储为00011100；-28即为10011100.

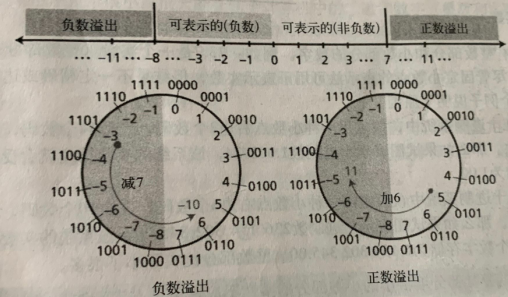
                 3）溢出：四位存储单元的溢出如图：

                                                                   

 

                4）符号加绝对值表示法的应用：存储部分实数，另外，符号加绝对值表示法通常用于采样模拟信号，如音频。

 

3.二进制补码表示法

 二进制补码表示法是计算机中用于存储整数的标准表示法。几乎所有的计算机都使用二进制补码表示法来存储位于n位存储单元的有符号整数。

                 1）在二进制补码表示法中，无符号整数的有效范围（0 - 2^n-1）被分成两个相等的子范围。第一个范围用于表示非负整数，第二个字范围用于表示负整数。如图为n为4的位模式：

                                                         左右交换，左负右正

 

    尽管整数的符号影响二进制整数存储时的每一位，但是最左边决定符号，如果最左位是 0 则为非负，如果最左位是 1 则为负数。

               2）反码和补码（针对二进制数）

                 反码：即取一个整数的反码。二进制所有位数取反。     

                补码：即取一个整数的补码。首先从右边复制位，直到有 1 被复制，剩下的数全部取反。

                故，对一个数进行两次补码或反码运算，都将得到原来的数。 

             3）二进制补码表示法仅有一个0.

             4）溢出：4位溢出如图.

                                                               

 

 

 

 

 

 

---存储实数

    实数的存储：浮点表示法，规范化，符号、指数和尾数，余码系统            带有很大的整数部分或很小的小数部分的实数不应该用定点表示法存储

1.浮点表示法      

用于维持正确度或精度的解决方法是使用浮点表示法。

       1）在浮点表示法中，无论十进制还是二进制，一个数字都由3部分组成：符号，位移，定点数。

      符号即+/-，可正可负；位移量即小数点应该左右移动构成实际数字的位移量；定点数即小数点位置固定的定点表示法。

      浮点表示法在科学中用于表示很小或很大的十进制数。在称作科学计数法的表示法中，定点部分在小数点左边只有 1 个数码而且位移量是10的幂次。

      例：一个数的科学技术法表示为    +7.425 x 10^21        

             这三部分分别为，符号（+），位移量（21），定点部分（7.425）。一些程序设计和计算器按照 +7.425E21 来显示该数字。

 

2.规范化：为了表示法的固定部分统一，科学计数法用于十进制，浮点表示法用于二进制，且都在小数点左边使用了唯一的非零数码，这称为规范化。

     十进制系统中的数码可能是1-9，二进制系统中该数码为1。

 

3.符号，指数和尾数 （尾数是小数点后面的位）

      例如：+1000111.0101 规范化后变成 +1.0001110101 x 2^6

                 其中符号（+），指数（6），尾数（0001110101）    注意小数点和定点部分左边的位1并没有存储，它们是隐含的。

4.余码系统

      尾数可以作为无符号数存储。指数是有符号的数。尽管这可以用二进制补码表示法来存储，但被一种称为余码系统的新的表示法取而代之。

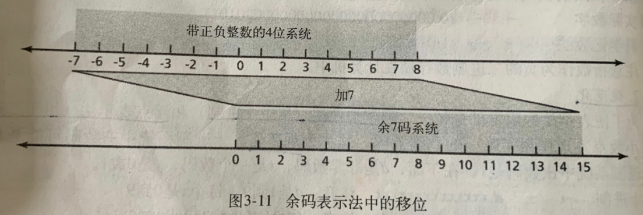
      在该余码系统中，正的和负的整数都可以作为无符号数存储。为了表示正的或者负的整数，将正整数（称为一个偏移量）添加到每个数字中，将它们统一移到非负的一边。

      这个偏移的量的值是2^ m-1 -1，m是内存单元存储指数的大小。如图

                                                         

 

5.单精度和双精度 

     单精度格式采用总共32位来存储一个浮点表示法的实数。符号占用1位（0正1负），指数占8位（使用偏移量127），尾数使用32位（无符号数）。也称余127码。

     双精度格式采用总共64位来存储一个浮点表示法的实数。符号占用1位，指数占用11位（使用偏移量位1023），尾数使用52位。也称余1023码。

    其他：上溢和下溢。

6.存储零：0.0这个特例中，符号，指数和尾数都设为0

7.截断误差：规范后多余位数被截断造成的与原数的误差称为截断误差。IEEE定义了用于更大尾数的其他表示法。