【HDU2815】【拓展BSGS】Mod Tree

Problem Description

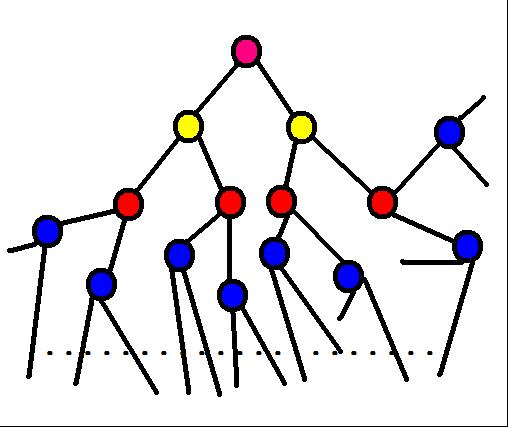
  The picture indicates a tree, every node has 2 children.
  The depth of the nodes whose color is blue is 3; the depth of the node whose color is pink is 0.
  Now out problem is so easy, give you a tree that every nodes have K children, you are expected to calculate the minimize depth D so that the number of nodes whose depth is D equals to N after mod P.

Input

The input consists of several test cases.
Every cases have only three integers indicating K, P, N. (1<=K, P, N<=10^9)

Output

The minimize D.
If you can’t find such D, just output “Orz,I can’t find D!”

Sample Input

78992 453
1314520 65536
1234 67

Sample Output

Orz,I can’t find D!
8
20

Author

AekdyCoin

Source

HDU 1st “Old-Vegetable-Birds Cup” Programming Open Contest

Recommend

lcy | We have carefully selected several similar problems for you: 2814 2809 3037 2447 2810

【分析】

普通的BSGS是只能够解决A^x = B(mod C),其中C为素数的形式，而通过网上的消元的方法能够解决这种问题。

同样BSGS直接解决C为素数的形式也是可以的.

 1 /*
 2 宋代晏几道
 3 《生查子·狂花顷刻香》
 4 狂花顷刻香，晚蝶缠绵意。天与短因缘，聚散常容易。
 5 传唱入离声，恼乱双蛾翠。游子不堪闻，正是衷肠事。 
 6 */ 
 7 #include <iostream>
 8 #include <cstdio>
 9 #include <ctime>
10 #include <cmath>
11 #include <algorithm>
12 #include <cstring>
13 #include <string>
14 #include <map>
15 #include <set>
16 #include <vector> 
17 #define LOCAL
18 const int MAXN = 1000 + 10;
19 const int INF = 0x7fffffff;
20 using namespace std;
21 typedef long long LL;
22 
23 int gcd(int a, int b ){return b == 0 ? a : gcd(b, a % b);}
24 int ext_gcd(int a, int b, int &x, int &y){
25     if (b == 0) {x = 1; y = 0; return a;}
26     int tmp = ext_gcd(b, a % b, y, x);
27     y -= x * (a / b);
28     return tmp;
29 }
30 //求解 
31 int Inval(int a, int  b, int n){
32     int x, y, e;
33     ext_gcd(a, n, x, y);
34     e = (LL) x * b % n;//小心超出int 的范围,因为a,n是互质的，因此求解出来的结果就是ax + ny = 1，乘以b才正确的答案 
35     return e < 0 ? e + n : e; 
36 }
37 // k s m
38 int pow_mod(LL a, int b, int c){
39     if (b == 1) return a % c;
40     LL tmp = pow_mod(a, b / 2, c);
41     if (b % 2 == 0) return (tmp * tmp) % c;
42     else return (((tmp * tmp) % c) * a) % c;
43 }
44 int BSGS(int A, int B, int C){
45     map<int, int> H;//hash
46     LL buf = 1 % C, D = buf, K;
47     int d = 0, tmp;
48     //小步
49     for (int i = 0; i <= 100; buf = buf * A % C, i++)
50     if (buf == B) return i;
51     //消因子 
52     while ((tmp = gcd(A, C)) != 1){
53           if (B % gcd(A, C) != 0) return -1;//为了解不定方程
54           d++;
55           C /= tmp;
56           B /= tmp;
57           D = D * A / tmp % C; 
58     }
59     H.clear();
60     int M = (int)ceil(sqrt(C * 1.0));
61     buf = 1 % C; 
62     for (int i = 0; i <= M; buf = buf * A % C, i++)
63     if (H.find((int)buf) == H.end()) H[(int)buf] = i;//Hash
64     
65     K = pow_mod ((LL) A, M, C);
66     for (int i = 0; i <= M; D = D * K % C, i++){
67         tmp = Inval((int) D ,B, C);//D和C是互质的 
68         //一定不要忘了最后的d 
69         if (tmp >= 0 && H.find(tmp) != H.end()) return i * M + H[tmp] + d;
70     } 
71     return -1;//找不到 
72 } 
73 int main(){
74     
75     //转换为A^x = B(mod C)的形式 
76     int A, B, C;
77     while (scanf("%d%d%d", &A, &C, &B) != EOF){
78           if (B >= C) {printf("Orz,I can’t find D!\n"); continue;}//233
79           int tmp = BSGS(A, B, C);
80           if (tmp < 0) printf("Orz,I can’t find D!\n");
81           else printf("%d\n", tmp);
82     }
83     return 0;
84 }
85 
86

View Code

posted @ 2015-03-20 08:27 TCtower 阅读(522) 评论(0) 编辑收藏举报

刷新页面返回顶部

【HDU2815】【拓展BSGS】Mod Tree

公告