【Ural1057】幂和的数量

【题目描述】

写一个程序来计算区间[X,Y]内满足如下条件的整数个数：它恰好等于K个互不相等的B的整数幂之和。

举个例子。令X=15，Y=20，K=2，B=2。在这个例子中，区间[15,20]内有3个整数恰好等于两个互不相等的2的整数幂之和：

17=2^4+2^0

18=2^4+2^1

20=2^4+2^2

【输入格式】

输入文件的第一行有两个空格隔开的整数X,Y（1<=X<=Y<=2^31-1）.

第二行有两个整数K,B（1<=K<=20,2<=B<=10）.

【输出格式】

输出一行一个整数，即[X,Y]中恰好等于K个互不相等的B的整数幂之和的数的个数。

【分析】

数位类统计，上一张图：

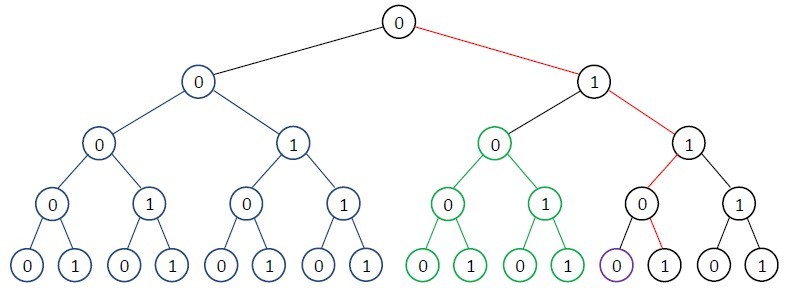
用f[i][j]来表示高度为i的二叉树下进制位有j个为1的数的个数。

对于询问n，我们需要求出不超过n的最大B进制表示只含0、1的数：
找到n 的左起第一位非0、1 的数位，将它变为1，并将右面所有数位设为1。（因为大于1的肯定不可取，后面置为1使它最接近原来的数）
将得到的B进制表示视为二进制进行询问即可。

 

#include <cstdio>
#include <iostream>
#include <cstring> 
int f[32][32];
int x,y,k,b;

int work(int x,int k);
int change(int x);
int main()
{
    int i,j;
    //初始化
    f[0][0]=1;
    for(i=1;i<=31;i++)
    {
        f[i][0]=f[i-1][0];
        for(j=1;j<=i;j++)
        f[i][j]=f[i-1][j]+f[i-1][j-1];
    }
    scanf("%d%d%d%d",&x,&y,&k,&b);
    printf("%d\n",work(change(y),k)-work(change(x-1),k));
    return 0;
}
int change(int x)
{
    int p=1,tot=0;
    while(x>=(long long)p*b) p*=b,++tot;//用来统计有tot个b进制位 
    int ans=0;
    //b进制转2进制 
    while(p && x/p<=1)
    {
          ans+=x/p*(1<<tot);
          tot--;
          x%=p;
          p/=b;
    }
    ans+=(1<<(tot+1))-1;
    return ans;
}
//统计[0..x]内二进制表示含k个1的数的个数
int work(int x,int k)
{
    //tot记录当前路径上已有的1的数量
    int ans=0,tot=0;
    for(int i=31;i;i--)
    {
        if(x&(1<<i))
        {
            ++tot;
            //跳出 
            if(tot>k)break;
            x^=(1<<i);
        }
        if((1<<(i-1))<=x)
        ans+=f[i-1][k-tot];
    }
    if(x+tot==k)++ans;
    return ans;
}