1 vj6补题
https://vjudge.net/contest/643996#overview
1) 几个点会被几个圆覆盖问题
重点
如何优化算法到1s:
不是遍历每个圆的每个点,我们移动圆心上下左右r。但这是个正方形区域,所以我们要判断距离是否超出圆的区域,然后标记每一个点
思路:
对于每个圆,使用双重循环遍历以圆心 (a, b) 为中心、半径 r 的正方形区域内的所有点。

代码1
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e4+500;
int n,m;
struct node
{
int a,b;
};
bool st[maxn][maxn]= {0};
vector<node> ve;
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1; i<=n; i++)
{
int a,b;
cin>>a>>b;
ve.push_back({a,b});
}
cin>>m;
while(m--)
{
int a,b,r;
cin>>a>>b>>r;
for(int i=0; i<=r; i++)
{
for(int j=0; j<=r; j++)
{
if(i*i+j*j<=r*r)
{
int aa=a-i;
int bb=b-j;
//(a-i, b-j) 是以 (a, b) 为中心,向左移动 i 个单位,向下移动 j 个单位得到的点
//通过圆心上下左右移动r实现标记圆周围的点
if(aa>=0&&bb>=0)
st[aa][bb]=1;
aa=a+i,bb=b-j;
if(aa>=0&&bb>=0)
st[aa][bb]=1;
aa=a-i,bb=b+j;
if(aa>=0&&bb>=0)
st[aa][bb]=1;
aa=a+i,bb=b+j;
if(aa>=0&&bb>=0)
st[aa][bb]=1;
}
}
}
}
int ans=0;
for(int i=0; i<ve.size(); i++)
if(st[ve[i].a][ve[i].b]==0)
ans++;
cout<<ans<<endl;
}
2)浮点数输出
cout<<fixed<<setprecision(3)<<a<<'\n';
3)贪心+multiset
题意:就是k个卡槽,每个卡槽可以录制一个视频,一个卡槽上的录制结束了马上可以录制下一个,问最多可以录制多少个视频。
思路:是以每一个视频为研究对象,看看他插在哪个插槽最合适。可以知道应该插在那个距离上一个结束时间最短的时候这样可以使得每一个插槽的利用率最大,所以此时可以又最优解。
重点
1.multiset允许重复元素,set与multiset均按照升序排列
2.pper_bound函数用于查找第一个大于给定值的元素的位置
代码
#include<stdio.h>
#include<iostream>
#include<string>
#include<algorithm>
#include<set>
using namespace std;
#define ll long long
const int N=1e5+10;
ll a[N];
struct node
{
ll be;
ll en;
bool operator <(node &a)
{
if(en!=a.en)
return en<a.en;
//按照结束时间排序 ,结构体要重载小于号
//最重要的转换:贪心策略是按照结束时间贪心
}
}b[N];
int main()
{
ll n,k,i,j;
cin>>n>>k;
multiset<int> se;
//不去重,并且从大到小排序
for(i=1;i<=n;i++)
{
cin>>b[i].be>>b[i].en;
}
std::multiset<int>::iterator it;
sort(b+1,b+1+n);
for(i=1;i<=k;i++)
{
se.insert(0);
//每个卡槽现在结束时间是0
}
ll ans=0;
for(i=1;i<=n;i++)
{
it=se.upper_bound(b[i].be);
/*
upper_bound(x)是找到第一个严格大于值,并返回其定位器),
得到该位置的上一个位置即为查找目标,记得特判定位器为begin()的情况,
指到它的前面会re */
if(it==se.begin())
continue;
//也就是卡槽里的结束时间都大于视频开始录制的时间
//这时这个视频就不能录制了,不特判会re
else
{
it--;
se.erase(it);
//se有k个元素,每个元素时每个卡槽的结束时间
//所以我们要删去i,这是由se元素代表每个卡槽的结束时间决定的
se.insert(b[i].en);
ans++;
}
}
printf("%lld\n",ans);
return 0;
}
4) 特殊的全排列
重点
1.递归的想法(全排列经常这么做把)
2.
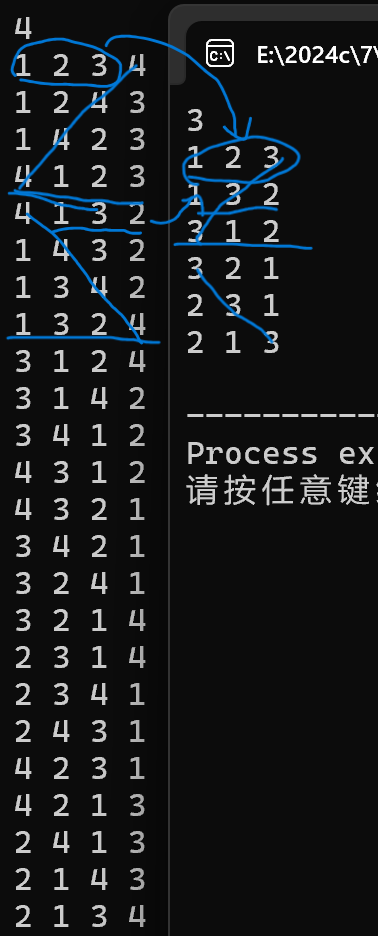
思路:我们可以得到所有全排列,只是要注意输出顺序,即相邻层不能移动太多,
n个数的全排列由n-1个数递归得到,所以比如3个数和四个数,先在右侧插入4,
再将这个数不断左移,到最前面,这个过程所有相邻排列的所有数都不会移动两次。
此时4在最前面,与左插正好只差了后三位,而又因为n=3时也保证了之移动一次,所以也满足。
题解1
代码
#include <iostream>
using namespace std;
int a[80000+10][8];//这么大是为了存1到8的结果
int main()
{
a[0][0]=1;
// a[i][j] 表示第 i 个排列中的第 j 个位置上的元素值。
int s=0; //当前i的开始位置,此时i为1
int end=0; //当前i的结尾位置
//s,end,跟踪每轮生成的范围
int n;
cin>>n;
for(int i=2; i<=n; i++)
//生成长度为i的排序
{
int len=end;
for(int j=s; j<=end; j++)
{
//遍历上一轮生成的排列
if((j-s)%2)//对应样例里面的从左插入
{
for(int t=0; t<i; t++)
{
//在位置t插入i然后将剩余元素向右移动
len+=1;
for(int k=0; k<t; k++)
a[len][k]=a[j][k];
//上一个结束时,已有len个排列,这时要生成第len+1个排列
//将以前的排列复制到新排列后面的位置
a[len][t]=i;
// 将3插入,即321
for(int k=t+1; k<i; k++)
a[len][k]=a[j][k-1];
//12354 先把5插入,然后复制123再复制4
}
}
else//对应从右插入
//先进行右插,所以为0时右插
{
for(int t=i-1; t>=0; t--)
{
len+=1;
for(int k=0; k<t; k++)
a[len][k]=a[j][k];
a[len][t]=i;
for(int k=t+1; k<i; k++)
a[len][k]=a[j][k-1];
}
}
}
s=end+1;//更新当前i的开始与结尾
end=len;
}
for(int i=s; i<=end; i++) //输出答案
{
for(int j=0; j<n-1; j++)
{
cout<<a[i][j]<<" ";
}
// 遍历第i个排列的所有位置输出这个排列
cout<<a[i][n-1]<<endl;
}
}
//3
//1 2 3
//1 3 2
//3 1 2
//3 2 1
//2 3 1
//2 1 3
)无向图连通(不懂没看
) 动态规划(不懂没看
2 cfdiv50补题
1) 地块划分(单调栈)
3 讲课二分
#include<bits/stdc++.h>
using namespace std;
int bs1(int l,int r)
{
while(l<r)
{
int mid=l+r>>1;
if(check(mid))
r=mid;
else
l=mid+1;
}
while(l<r)
{
int mid=l+r+1>>1;//尽量向右找需要+1
if(check(mid))
l=mid;
else
r=mid-1;
}
double l,r;
double eps=1e-5;
while(r-l<eps)
{
double mid=(l+r)/2
if(check(mid))
l=mid;
else
r=mid;
}
}
1)路标设置(枚举+二分答案)
https://www.luogu.com.cn/problem/solution/P3853
题意:
政府在一条长度为 l 的公路上放置 n个路标,并且最多可以增设 k 个路标。目标是找到一个最小的最大间隔,使得所有相邻路标之间的间隔不超过这个最大间隔。

点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n, k, l = 1, r, ans;//记得初始化 l
int a[100001];
int main()
{
cin >> r >> n >> k;
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
while (l <= r) {
int mid = (l + r +1)/ 2;
//判断是否可以通过增设不超过 k 个路标,使得最大间隔不超过 mid
int m = 0;
for (int i = 1; i < n; i++) {
int flag = a[i] - a[i - 1];
if (flag > mid) m += (flag - 1) / mid; //计算需要增设的路标数量
}
// 如果可以通过增设不超过 k 个路标满足条件,则更新答案并缩小搜索范围
if (m <= k) {
ans = mid;
r= mid-1 ;
} else l=mid+1;
}
cout << ans;
return 0;
}
2)贪心+二分+优先队列
https://www.luogu.com.cn/problem/P9559
题目:
对于一个运动员 i ,他的速度是 vi,体重是 wi。如果运动员 j 的体重 wj <= wi,那么运动员 i 可以用原本的速度 vi 背着运动员 j 奔跑。如果 wj > wi,那么速度就变成了 vi - ( wi - wj ) (如果是负数,那么运动员 i 不能背着 j 奔跑)。
给定一个T,代表有T组数据。每组数据第一行输入一个n,代表这个团队有n个人,后面n行,每行两个数vi,wi。运动员可以被背着跑,也不能不背着人跑。求这个团队奔跑起来后速度最慢的那个人 的速度最大值。
重点:
1.思路:速度越大的背越重的

2.优先队列默认大顶堆,优先输出最大元素
代码
#include<bits/stdc++.h>
using namespace std;
struct node{int v,w;}t[100005];
inline bool cmp(node a,node b){return a.v<b.v;}
int T,n,l,r,mid,ans;
inline bool check(int x)
{
priority_queue<int>l,r;
for(int i=1;i<=n;++i)
{
if(t[i].v>=x) r.push(t[i].w+t[i].v);//分成两个部分,速度满足条件的要看速度和体重之和
else l.push(t[i].w);//速度不满足的只看体重
}
while(!l.empty()&&!r.empty())
if(r.top()-l.top()>=x) l.pop(),r.pop();//每次看最大的一组人是否满足条件
//速度和体重和大的去背体重大的。即队头对队头
else return 0;
return (l.empty());//如果最后剩的是速度低的人也不满足条件
}
int main()
{
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d%d",&t[i].v,&t[i].w);
sort(t+1,t+n+1,cmp),l=0,r=1000000000,ans=0;
//按照速度大小排序
while(l<=r)//这里也是小于等于,所以类似的我们
//在更新时mid+1,mid-1;
{
//枚举最小速度的最大值
mid=l+r>>1;
if(check(mid)) l=mid+1,ans=mid;
else r=mid-1;
}
printf("%d\n",ans);
}
}
3)跳石头(贪心+二分
重点
虽然起点和终点不能移动,但还是要判断是否符合这个距离。
另外还要考虑连续几块石头都要移走
代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#define M(a) memset(a,127,sizeof a)
#define fo(j,n) for(i=j;i<=n;i++)
using namespace std;
int i,L,N,M,a[50010];
int check(int dist){//检验函数,求出给定距离dist后 需要移走多少石头,是否不超过M
int i,last=0,cnt=0;
for(i=1;i<=N;i++){
if(a[i]-last<dist)cnt++;
else last=a[i];
}
if(L-last<dist)cnt++;
//特判终点
return cnt<=M;
}
int main(){
scanf("%d %d %d",&L,&N,&M);
for(i=1;i<=N;i++)scanf("%d",a+i);
sort(a+1,a+1+N);
int lo=1,hi=L+1,mid;
while(lo<hi){//二分查找模板
//没取等
mid=(lo+hi+1)/2;
//找右边界
if(check(mid))lo=mid;
else hi=mid-1;
}
printf("%d\n",lo);
}
4) 区间查找(二分/stl)
1.vector的begin返回第一个元素的位置,end返回的是最后一个元素的下一个位置!!!
2.count函数是o(n)的,所以一般用lower和upper实现查找
3.count左闭右开所以要传入r+1;
正确
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
vector<int> a[N];
int main() {
int n;
while (cin >> n) {
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
a[x].push_back(i);
}
int m;
cin >> m;
while (m--) {
int l, r, x;
cin >> l >> r >> x;
int L = lower_bound(a[x].begin(), a[x].end(), l) - a[x].begin();
int R = lower_bound(a[x].begin(), a[x].end(), r) - a[x].begin();
int f = 0;
if (L != a[x].size()) {
if (R == a[x].size()) {
f = a[x].size() - 1 - L + 1;
} else {
if (a[x][R] > r)
R--;
f = R - L + 1;
}
}
if (f)
cout << f << endl;
else
cout << "666666!" << endl;
}
cout << endl;
}
return 0;
}
tle代码
#include<bits/stdc++.h>
using namespace std;
vector<int> a;
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int n;
cin>>n;
a.push_back(0);
for(int i=1;i<=n;i++)
{int x;
cin>>x;
a.push_back(x);
}
int m;
cin>>m;
while(m--)
{int x,l,r;
cin>>l>>r>>x;
// cout<<*a.begin()<<" "<<*(a.end()-1)<<endl;
//for(auto it=a.begin()+l;it!=a.begin()+r+1;it++)
//{
// cout<<"*"<<*it<<endl;
//}
if(count(a.begin()+l,a.begin()+r+1,x)==0)
cout<<"666666!"<<endl;
else
cout<<count(a.begin()+l,a.begin()+r+1,x)<<endl;
}
}



