算法竞赛(二分) (上午)
图论+二分
//邻接表实现无边权
vector<int> g[maxn];
g[x]push_back(y);
g[y]push_back(x);
//边权实现
#include <vector>
using namespace std;
const int maxn = 1000; // 最大节点数
vector<pair<int, int>> g[maxn]; // g[i] 表示节点 i 的邻接表,pair<int, int> 中第一个 int 是相邻的节点,第二个 int 是边的权重
void addEdge(int x, int y, int z) {
g[x].push_back({y, z}); // 添加边 x -> y,权重为 z
g[y].push_back({x, z}); // 添加边 y -> x,权重为 z(无向图)
}
//题解
#include<bits/stdc++.h>
using namespace std;
const int N = 10010;
long long f[N];//点的费用
vector< pair< int , long long> >vec[N];//存边
priority_queue< pair< long long, int > >que;
int vis[N];
long long dis[N];
long long b, v;
int n, m, x, y;
int check(int x)
{
if(f[1] > x) return 0;//如果第一个点就不能走,直接返回不行
for(int i = 1; i <= n; ++ i){
dis[i] = 1e18;//必备的初始化,没有会致错
vis[i] = 0;
}
dis[1] = 0;
que.push(make_pair(0, 1));//修改的dijk
while(!que.empty()){
int u = que.top().second;
que.pop();
if(vis[u]) continue;
vis[u] = 1;
for(int i = 0; i < vec[u].size(); ++ i){
int v = vec[u][i].first;
if(f[v] > x) continue;//如果新拓展的点不符合要求,继续寻找
long long w = vec[u][i].second;
if(dis[u] + w < dis[v]){
dis[v] = dis[u] + w;
que.push(make_pair(-dis[v], v));
if(v == n){//如果已经到达,判断是否生命值有剩余
if(dis[n] >= b) return 0;
else return 1;
}
}
}
}
return 0;//如果没有到达,直接返回不行
}
int main()
{
long long mxx = -1;
scanf("%d%d%lld", &n, &m, &b);
for(int i = 1; i <= n; ++ i){
scanf("%lld", &f[i]);
mxx = max(mxx, f[i]);//寻找上边界
}
for(int i = 1; i <= m; ++ i){
scanf("%d%d%lld", &x, &y, &v);
vec[x].push_back(make_pair(y, v));
vec[y].push_back(make_pair(x, v));
}
long long ans = -1, l = 1, r = mxx;
while(l <= r){
long long mid = (l + r) / 2;
if(check(mid)) ans = mid, r = mid - 1;//更形ans
else l = mid + 1;
}
if(ans == -1) puts("AFK");//如果每次都没有扩展成功说明不能到达
else printf("%lld\n", ans);
return 0;
}
//初始化方式
// 使用 make_pair
vec[0].push_back(std::make_pair(1, 2));
// 使用列表初始化
vec[1].push_back({3, 4});
二分进击奶牛
点击查看代码(自己写的tle)
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,c;
int a[maxn]= {0};
int d[maxn];
bool check(int mid)
{
int cnt=0;
for(int i=1; i<=n; i++)
if(d[i]<mid)cnt++;
if(cnt>=c)
return false;
return true;
}
int bs(int l,int r)
{
while(l<r)
{
int mid=(l+r+1)>>1;
if(check)
r=mid;
else
l=mid+1;
}
return l;
}
int main()
{
cin>>n>>c;
for(int i=1; i<=n; i++)
{
cin>>a[i];
d[i]=a[i]-a[i-1];
}
cout<<bs(1,maxn/2);
return 0;
}
1.没排序2.取出一个牛后没有更新距离3.好像破坏了d[i]数组?
最后其实是因为理解错题目了,是c头牛,、
然后就是<c,=c,>c,当我们要找最右侧的等于c,我们应该从这点分开,分成>c和<=c,两段才好。
算法竞赛(二分)(下午)
实数二分
#define eps=1e-5;
double pi=acos(-1.0);
分蛋糕
http://poj.org/problem?id=3122
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define ms(x, n) memset(x,n,sizeof(x));
typedef long long LL;
const int inf = 1<<30;
const LL maxn = 1e4+10;
const double pie = 3.1415926535897932;
const double eps = 1e-8;
int N, F;
double a[maxn];
bool check(double r){
//所有派是否可以分成F份半径为r的
int cnt = 0;
for(int i = 1; i <= N; i++)
//a[i]最多内可以划分几个r半径的小圆
cnt += (int)(a[i]/r); //内接圆公式
return cnt >= F;
}
int main()
{
int T;
scanf("%d",&T);
while(T--){
double sum = 0;
scanf("%d%d",&N,&F);
++F;
for(int i = 1; i <= N; i++){
scanf("%lf",&a[i]);
a[i] *= a[i];
sum += a[i];
}
double l = 0, r = sum/F, mid;
while(r-l > eps){
mid = (l+r)/2;
if(check(mid)) l = mid;
else r = mid;
}
printf("%.4lf\n", pie*l);
}
return 0;
}
寻找第k小的数(优化)
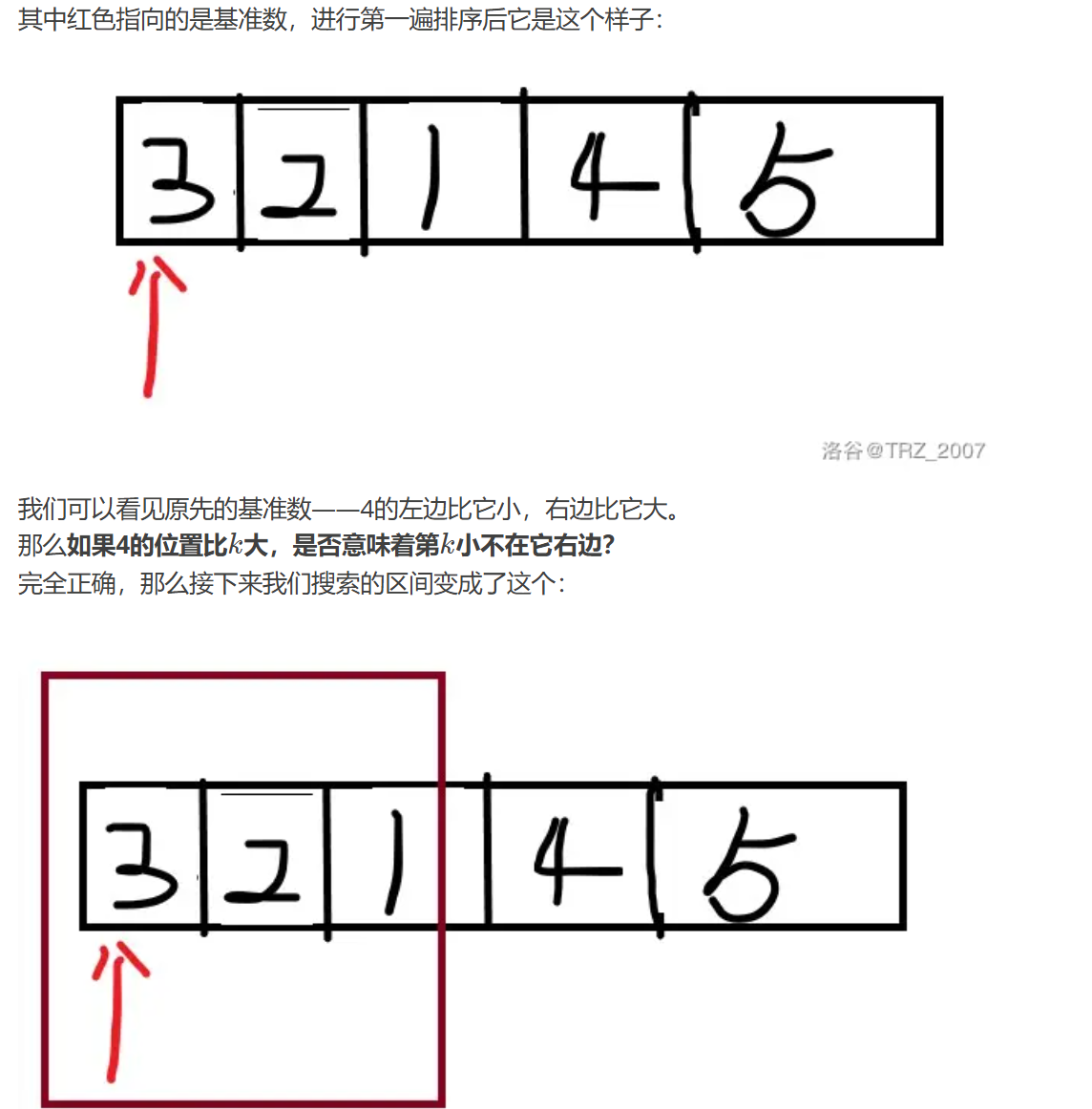
stl

课后例题
1 线性动态规划(butaidong
https://www.luogu.com.cn/problem/P1868

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
vector<int>beg[3000010];//有点大,不过并不会 MLE
int n,mx,f[3000010];//mx 代表最大的 y,f 就是 dp 用的数组
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x,y;
scanf("%d%d",&x,&y);
beg[y].push_back(x-1);//这里保存的是 x-1,后面会比较方便
mx=max(mx,y);
}
for(int i=1;i<=mx;i++){
f[i]=f[i-1];//先设定为 f[i-1],后面再更新
for(int j=0;j<beg[i].size();j++){
int b=beg[i][j];
f[i]=max(f[i],f[b]+i-b);//这里会比较方便
}
}
printf("%d\n",f[mx]);
return 0;
}
二分+前缀和 质检员
https://www.luogu.com.cn/problem/P1314
#include<bits/stdc++.h>
using namespace std;
const int maxn=200010;
int w[maxn],v[maxn],l[maxn],r[maxn];
long long pre_n[maxn],pre_v[maxn];
long long Y,s,sum;
int n,m,mx=-1,mn=2147483647;
bool check(int W)
{
Y=0,sum=0;
memset(pre_n,0,sizeof(pre_n));
memset(pre_v,0,sizeof(pre_v));
for(int i=1;i<=n;i++)
{
if(w[i]>=W) pre_n[i]=pre_n[i-1]+1,pre_v[i]=pre_v[i-1]+v[i];
else pre_n[i]=pre_n[i-1],pre_v[i]=pre_v[i-1];
}
for(int i=1;i<=m;i++)
Y+=(pre_n[r[i]]-pre_n[l[i]-1])*(pre_v[r[i]]-pre_v[l[i]-1]);
sum=llabs(Y-s);
if(Y>s) return true;
else return false;
}
int main(){
// freopen("qc.in","r",stdin);
// freopen("qc.out","w",stdout);
scanf("%d %d %lld",&n,&m,&s);
for(int i=1;i<=n;i++)
{
scanf(" %d %d",&w[i],&v[i]);
mx=max(mx,w[i]);
mn=min(mn,w[i]);
}
for(int i=1;i<=m;i++)
scanf(" %d %d",&l[i],&r[i]);
int left=mn-1,right=mx+2,mid; //这里有的人说要特判左右端点的check,但是其实你把left开成mn-1,right开成mx+2(注意取mx+1时即为W比所有都大,Y是0,这个情况要考虑,所以+2包含mx+1)就可以包含左右端点的check了,会简单点。
long long ans=0x3f3f3f3f3f3f3f3f;//ll 范围内的无穷大,近似于(maxll/2)的大小
while(left<=right)
{
mid=(left+right)>>1;
if(check(mid)) left=mid+1;
else right=mid-1;
if(sum<ans) ans=sum;
}
printf("%lld",ans);
return 0;
}
图论(今日讲课)
floyd
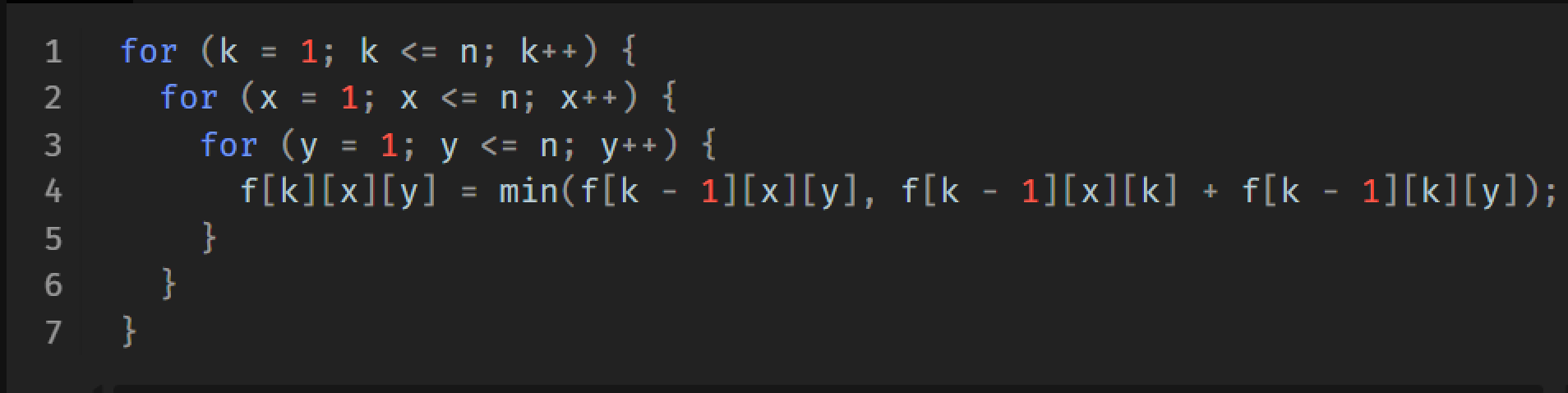
初始化:
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
// 算法结束后,d[a][b]表示a到b的最短距离
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}


邻接矩阵通常用于顶点较少的图,或者边的个数接近顶点个数的平方的图,也就是稠密图。
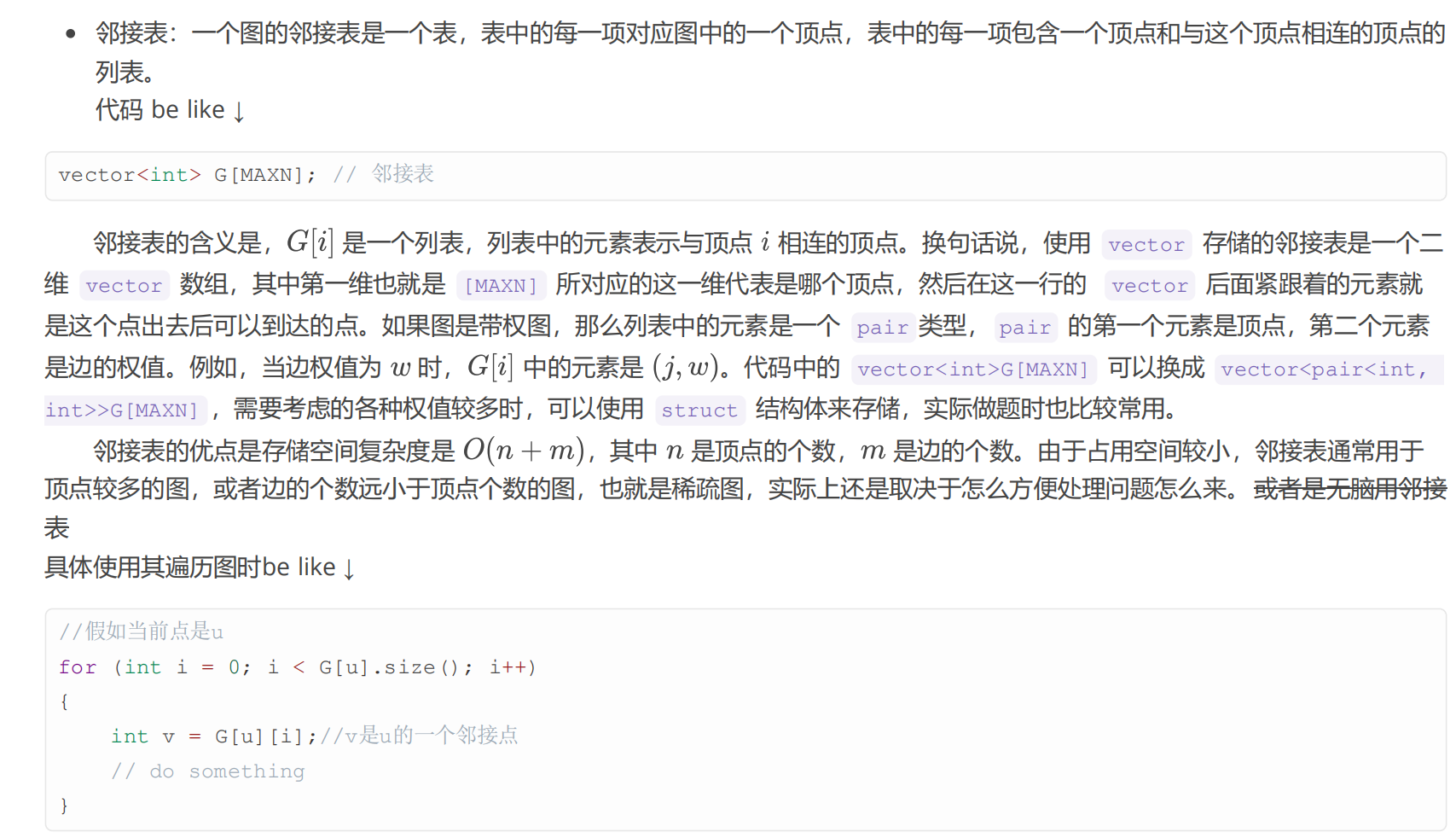
//假如当前点是u,使用其实现Dijkstra算法的松弛操作为例
for (auto v : G[u])
{
if (dis[v.first] > dis[u] + v.second)
{
dis[v.first] = dis[u] + v.second;
que.push({dis[v.first], v.first});
}
}
【金山文档 | WPS云文档】 图论基础
https://kdocs.cn/l/cjaYim9ZI71R



