DP-leetcode53-最大子序和(dp和分治法)

题目：

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

思路：

连续子数据就是一个开始和结尾的区间，可以把当前元素作为区间的结尾来判断的话

以 i 结尾的所有子数组中，和最大的是多少？

如果 i-1<0 那么nums[i] 自己变成一个子数组，因为是取最大值，不能越加越小。

如果 i-1 > 0 那么就是i-1的最大和的值上加当前的值

所以归为两种状态：

​ 1. nums[i]

​ 2. dp[i-1] + nums[i]

​ 下一步是获取最大值，max（nums[i] + dp[i-1]， nums[i]）

时间复杂度O(n)

解题：

def maxSubArray(self, nums):
    if not nums:
        return 0
    res =  nums[0] #记录最大值
    for i in range(1,len(nums)):
        nums[i] = max(nums[i-1]+nums[i], nums[i])
        res = max(nums[i], res)
        return res

进阶:

分治法求解:O(nlogn)

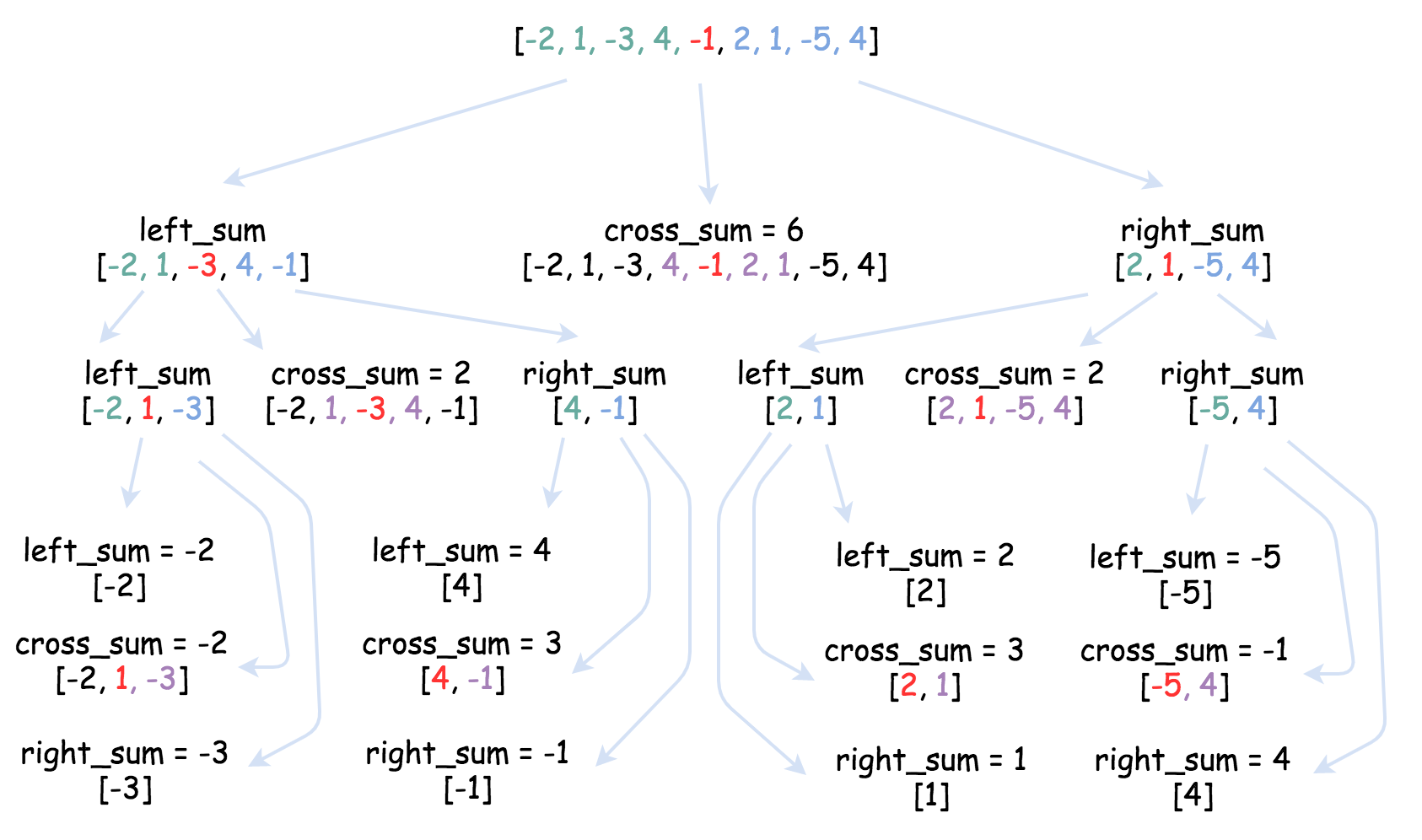
借用一下官方大佬的图图；

分而治之、拆分成多个小数组、并获取最大值 最后合并最大值返回。

def cross_sum(nums, left, right, p): 
    if left == right:
        return nums[left]

    left_subsum = float('-inf')
    curr_sum = 0
    for i in range(p, left-1, -1):
        curr_sum += nums[i]
        left_subsum = max(left_subsum, curr_sum)

    right_subsum = float('-inf')
    curr_sum = 0
    for i in range(p + 1, right + 1):
        curr_sum += nums[i]
        right_subsum = max(right_subsum, curr_sum)

    return left_subsum + right_subsum

def helper(nums, left, right):
    if left == right:
        return nums[left]
    
    p = (left + right) // 2
    left_sum = helper(nums, left, p)
    right_sum = helper(nums, p + 1, right)
    cross_sum1 = cross_sum(nums, left, right, p)
    return max(left_sum, right_sum, cross_sum1)

nums = [-2,1,-3,4,-1,2,1,-5,4] 
a = helper(nums, 0, len(nums) - 1)