常见树的总结

树

BST

Binary Sort Tree：二叉查找树，或二叉搜索树，或二叉排序树

性质：

  • 若左子树不空，则左子树上所有结点的值均小于它的根结点的值；

  • 若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；

  • 左、右子树也分别为二叉查找树；

  • 没有键值相等的节点。

**特点：**对二叉查找树的中序遍历，是升序的序列。查找的时间复杂度 O(logN)，最坏的情况下退化至O(N)，因此出现了各种平衡二叉树，以最求优雅的O(logN)。

二叉查找树的插入过程如下：

  • 若当前的二叉查找树为空，则插入的元素为根节点;

  • 若插入的元素值小于根节点值，则将元素插入到左子树中;

  • 若插入的元素值不小于根节点值，则将元素插入到右子树中。

AVL

平衡二叉树：（Balanced Binary Tree），平衡的BST，以发明人命名，AVL（Adelson-Velskii and Landis）

性质：如果每一个节点的左子树和右子树的高度差不超过1，那么这可树就是平衡二叉树。

特点：判断一个树是否为平衡树，把握三点。递归判断 （1）左子树是否平衡 （2）右子树是否平衡 （3）左子树的高度和右子树的高度差值低于1。查找的时间复杂度，严格的O(logN)。优雅的解决了BST退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。

缺点：频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对BST来说，时间上稳定了很多。

自平衡操作：4种情况的失衡状态，两两对称

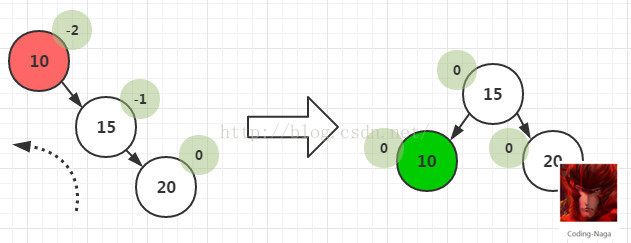
  • 1）LL型：如果在一个节点的左子树的左子树上插入一个新节点。方法：将节点右旋使其平衡。

img

​ 原A的左孩子B变为父结点，A变为其右孩子，而原B的右子树变为A的左子树，注意旋转之后Brh是A的左子树。

img

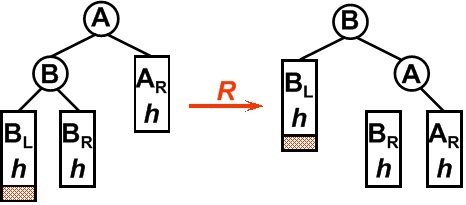
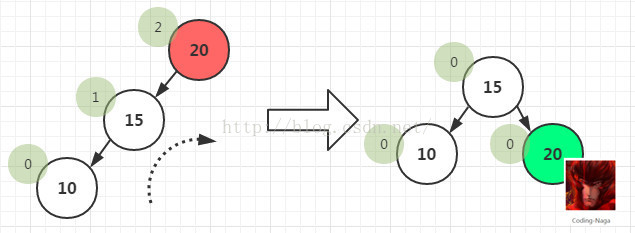
  • 2）RR型：在一个节点的右子树的右子树上插入一个新节点。方法：将节点左旋使其平衡。

img

​ 原A右孩子B变为父结点，A变为其左孩子，而原B的左子树Blh将变为A的右子树。

img

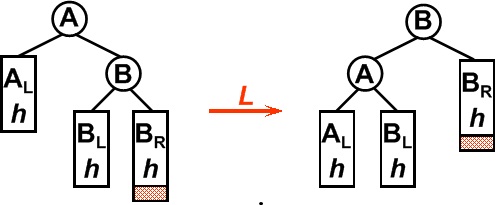
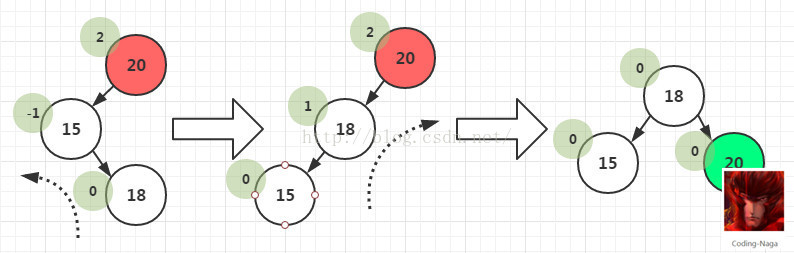
  • 3）LR型：在一个节点的左子树的右子树上插入一个新节点。方法：双旋转，两步走，先让树中高度较低的进行一次左旋，这个时候就变成了LL型了。再进行一次右旋操作即可。

img

在B节点按照RR型向左旋转一次之后，二叉树在A节点仍然不能保持平衡，这时还需要再向右旋转一次。

img

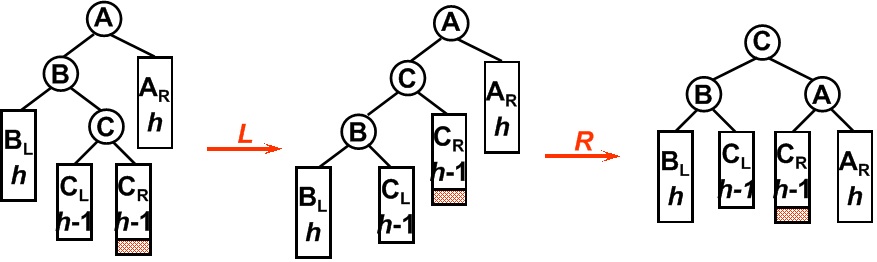
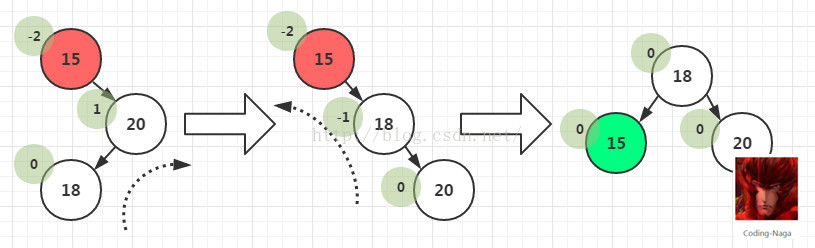
  • 4）RL型：在一个节点的右子树的左子树上插入一个新节点。方法：双旋转，先让树中高度较低的进行一次右旋，这个时候就变成了RR型了。再进行一次左旋操作即可。

img

与LR情况刚好相反，将B结点右旋，变为RR，再让A结点单左旋。

img

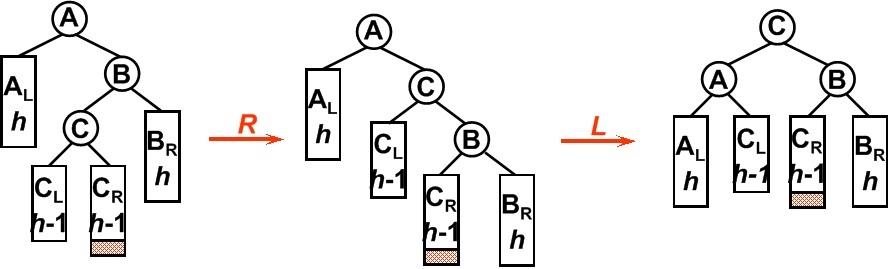
R-B Tree

红黑树：是一种自平衡二叉查找树，复杂且高效，并且在实践中是高效的: 它可以在O(logn)时间内做查找，插入和删除。红黑树还是2-3-4树的一种等同，它们的思想是一样的，只不过红黑树是2-3-4树用二叉树的形式表示的。

性质：五大性质

  • 1）所有节点都是 红色 或者 黑色，非红即黑。

  • 2）根节点是黑色

  • 3）红色节点的子节点不能是红色，必须是黑色

  • 4）所有的NIL结点都是黑色（注：为空的叶子节点）

  • 5）从任意节点出发，所有到NIL节点的路径含有相同数量的黑色节点

如下图所示：

img

红黑树基本操作（一）：添加节点

​ 大致步骤，将红黑树当作一颗二叉查找树，将节点插入；然后，将节点着色为红色；最后通过旋转和重新着色等方法，来修正，使之成为一颗满足五大性质的红黑树。

​ 可分为三大情况来处理：

  • 情况1：插入节点的是根节点。方法：直接把这个节点涂为黑色

  • 情况2：插入节点的的父节点是黑色。方法：无任何操作，仍是红黑树。

  • 情况3：插入结点的父节点是红色，又分为三种小情况：

    • case 1）情况：当前节点的父节点是红色，叔叔节点也是红色。 方法：1、将“父节点”设为黑色。2、将“叔叔节点”设为黑色。3、将“祖父节点”设为红色。4、将“祖父节点”设为“当前节点”；即，之后的操作，继续转化为对“当前节点”的操作。

img

  • case 2）情况：当前节点的父节点是红色，叔叔节点是黑色，且当前节点是其父节点的右孩子

​ 方法：1、将“父节点”作为“新的当前节点”。2、以”新的当前节点“为支点进行左旋。

img

  • case 3）情况：当前节点的父节点是红色，叔叔节点是黑色，且当前节点是其父节点的左孩子

​ 方法：1、将“父节点”设为黑色。2、将“祖父节点”设为红色。3、以“祖父节点”为支点进行右旋

img

红黑树的基本操作（二）：删除

​ 大致步骤，将红黑树当作一颗二叉查找树，将该节点从二叉查找树中删除；然后，通过旋转和重新着色等操作来修复成红黑树，使之重新成为一颗红黑树。

​ 第一步：

  • 情况1：被删除的节点没有孩子，即为叶节点（注：不是NIL节点）。方法：直接删除该节点

  • 情况2：被删除的节点只有一个孩子。方法：直接删除该节点，那么该孩子直接顶替它的位置。

  • 情况3：被删除的节点有两个孩子。则找到“当前节点”的“后继节点”，把“后继节点”复制给“当前节点”，覆盖它。然后删除后继节点。即问题往下转移，直至遇到情况1，和情况2，停止。

​ 第二步：

​ 修复红黑树，通过旋转和重新着色，使之重新成为一颗红黑树。

B-tree

B-tree即B树，B-树，又叫平衡多路查找树。

一颗m阶的B树（m叉树）的特性如下：

  • 1、树中每个节点最多含有m个孩子；

  • 2、除根节点和叶子结点外，其他每个节点至少有[ceil(m/2)]个孩子（其中ceil(x)是一个取上限的函数）；

  • 3、若根节点不是叶子结点，则至少有两个孩子（特例：整棵树只有一个节点）；

  • 4、所有的叶子结点都出现在同一层，叶子结点为NULL，即NIL节点；

  • 5、有j个孩子的非叶节点恰好有j-1个关键码，关键码按递增次序排列；

备注：B树中的每个结点根据实际情况可以包含大量的关键字信息和分支(当然是不能超过磁盘块的大小，根据磁盘驱动(disk drives)的不同，一般块的大小在1k~4k左右)；这样树的深度降低了，这就意味着查找一个元素只要很少结点从外存磁盘中读入内存，很快访问到要查找的数据。

img

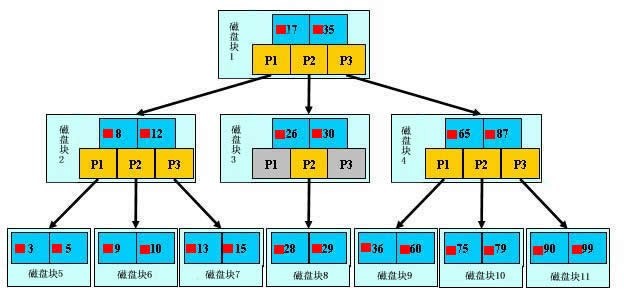
B+tree

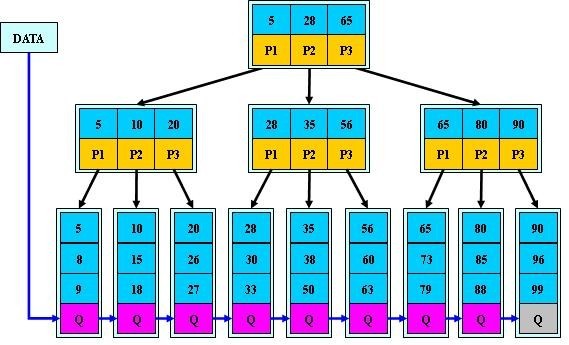
B+树，是应文件系统所需而产生的一种B-tree的变形树。

与B树的差异在于：

  • 1、有n棵子树的节点含有n个关键字；（而B树是n棵子树有n-1个关键字）

  • 2、所有叶子结点中包含了全部关键字的信息，即指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小，自小到大的顺序链接。（而B树的叶子节点并没有包括全部需要查找的信息）

  • 3、所有的非终端节点可以看成是索引部分，节点中仅含有其子树根节点中最大（或最小的关键字）。而B树的非叶子结点也包含需要查找的有效信息。

img

问题： 为什么说B±tree比B 树更适合实际应用中操作系统的文件索引和数据库索引？

  1. B±tree的磁盘读写代价更低

B±tree的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。

​ 举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B+ 树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B 树就比B+ 树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

  1. B±tree的查询效率更加稳定

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

SB-Tree

SB-Tree：Size Balanced Tree，自平衡条件：每个结点所在子树的结点个数不小于其兄弟的两个孩子所在子树的结点个数。

与AVL树的差异：

​ AVL 树比较的是层数，而SB 树比较的是 Size ，结点的多少。另一个和 AVL 不太一样的是，SBTree 只有在插入时才可能触发调整，而不需要在删除结点以后进行调整。

插入时的调整：与AVL树类似，分为LL，RR，LR，RL，四种情况。

TireTree

字典树，又称前缀树解决字符串前缀匹配问题，查找单词是否存在，统计以如“abc”开始的字符串的个数，实现词频统计等。

public static class TrieNode {
	public int path;   // 记录有多少个字符经过
	public int end;    // 记录有多少个字符串以此节点结尾
	public TrieNode[] nexts;  // 路
		public TrieNode() {
			path = 0;
			end = 0;
			nexts = new TrieNode[26];
		}
	}
posted @ 2019-04-06 17:37  Horken  阅读(172)  评论(0)  编辑  收藏  举报