【JZOJ6277】矩阵游戏

description

---

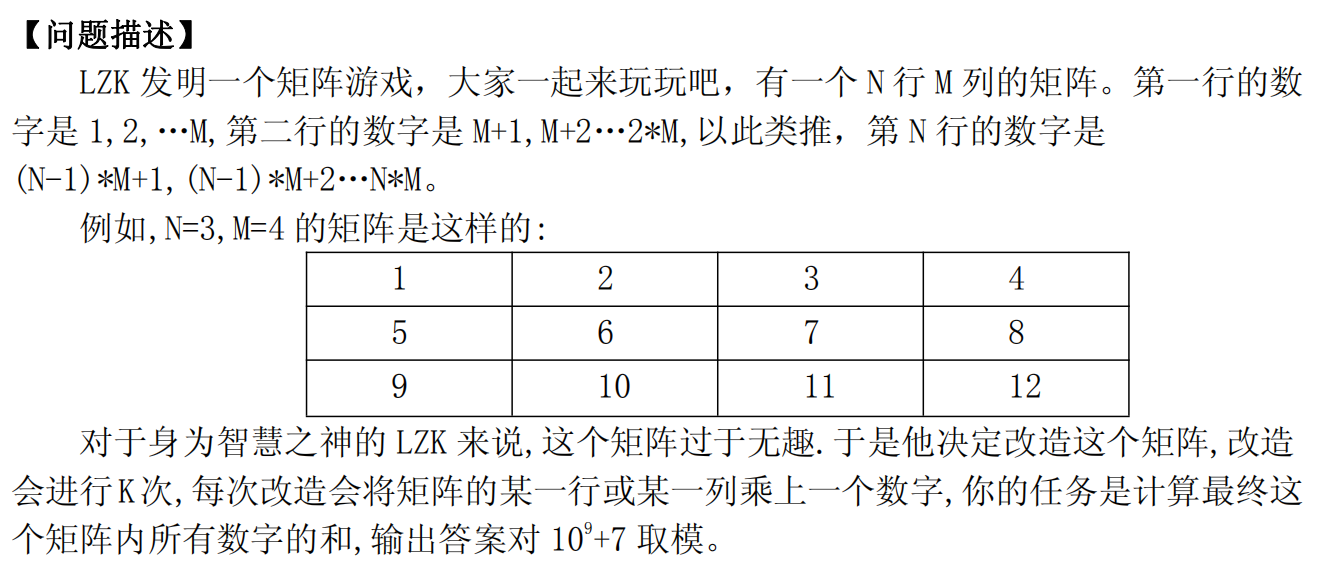
analysis

• 设所有操作之后，\(f[i]\)表示\(i\)行乘的数，\(g[j]\)表示\(j\)列乘的数，那么

\[Answer=\sum^{n}_{i=1}\sum^{m}_{j=1}[m*(i-1)+j]*f[i]*g[j] \]

• 中括号里的就是该位置原来的数，很好理解，然后移项

\[=\sum_{i=1}^{n}f[i]\sum_{j=1}^mg[j]*m*(i-1)+g[j]*j \]

\[=\sum_{i=1}^n\{f[i]*(i-1)*m*\sum_{j=1}^mg[j]+f[i]*\sum_{j=1}^mg[j]*j\} \]

• 然后就没了

---

code

#pragma GCC optimize("O3")
#pragma G++ optimize("O3")
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define MAXN 1000005
#define mod 1000000007
#define mo mod
#define ll long long
#define reg register ll
#define fo(i,a,b) for (reg i=a;i<=b;++i)
#define fd(i,a,b) for (reg i=a;i>=b;--i)

using namespace std;

ll f[MAXN],g[MAXN];
ll n,m,k,sigma,sum,ans;
char s[5];

inline ll read()
{
	ll x=0,f=1;char ch=getchar();
	while (ch<'0' || '9'<ch){if (ch=='-')f=-1;ch=getchar();}
	while ('0'<=ch && ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*f;
}
int main()
{
	freopen("T1.in","r",stdin);
	//freopen("game.in","r",stdin);
	//freopen("game.out","w",stdout);
	n=read(),m=read(),k=read();
	fo(i,1,n)f[i]=1;fo(i,1,m)g[i]=1;
	while (k--)
	{
		scanf("%s",&s);
		ll x=read(),y=read();scanf("\n");
		if (s[0]=='R')f[x]=(f[x]*y)%mod;
		else g[x]=(g[x]*y)%mod;
	}
	fo(i,1,m)sigma=(sigma+g[i])%mod,sum=(sum+g[i]*i)%mod;
	fo(i,1,n)ans=(ans+(f[i]%mod*(i-1)%mod*m%mod*sigma%mod+f[i]%mod*sum%mod)%mod)%mod;
	printf("%lld\n",ans);
	return 0;
}