【JZOJ3238】【BZOJ3482】超空间旅行
description
在遥远的未来,行星之间的食品运输将依靠单向的贸易路线。每条路径直接连接两个行星,且其运输时间是已知的。
贸易商协会打算利用一项最近发现的新技术——超空间旅行,以增加一些新的航线。通过超空间旅行的航线也是单向的。由于该项技术仍处于试验阶段,超空间旅行的时间目前是未知的,但它不取决于行星之间的距离,所以每个超空间旅行的路线将花费等量的时间。
下图是三个相互联通的行星及其运输时间的例子。行星使用正整数标号,超空间旅行时间记为“x”(图片对应第二个输入样例):
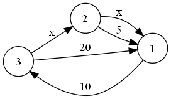
运输时间以天计,并且始终是一个正整数。
贸易商协会希望对引进新航线的结果进行分析:对于某两个行星A和B,他们想知道对于任意的x,从A到B的最短路径的总运输时间的所有可能的值。例如,在上述情况中,从星球2到星球1的最短路径所需时间可以取值5(如果x≥5),4,3,2,或1天(如果x<5)
analysis
-
最短路\(+\)凸包
-
对于一条路径,肯定是\(0x+b_0,x+b_1,2x+b_2\)这样的一次函数
-
可以先跑最短路,\(f[i][j]\)表示到从\(S\)开始到第\(i\)位经过了\(j\)条\(x\)边的最小常数值
-
若\(f[T]\)全为\(∞\),则无解;若\(f[T][0]\)为\(∞\),即没有一条确定值的路径,则有无数解
-
跑完最短路,得到了一些一次函数,然后栈维护一个上凸壳
-
若栈顶与当前函数交点的横坐标小于栈顶两个函数交点的横坐标,则该函数更优,不断出栈即可
-
求出一个上凸壳后,函数两两交点之间的线段即为某函数的贡献值,计算求和
-
注意算上常值函数的贡献
-
本子\(OJ\)艹过去了,垃圾\(JZOJ\)对\(dij\)的优先队列极不友好所以\(T\)飞了
-
感觉最近思维僵化,这个最短路模型和记几没有结合一起思考,还要再多巩固一下记几知识
code
#pragma GCC optimize("O3")
#pragma G++ optimize("O3")
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<queue>
#define MAXN 505
#define MAXM 20005
#define INF 1000000007
#define ll long long
#define reg register ll
#define fo(i,a,b) for (reg i=a;i<=b;++i)
#define fd(i,a,b) for (reg i=a;i>=b;--i)
#define rep(i,a) for (reg i=last[a];i;i=next[i])
using namespace std;
ll last[MAXM],next[MAXM],tov[MAXM],len[MAXM];
ll f[MAXN][MAXN];
ll n,m,q,tot,S,T;
bool bz[MAXN];
struct node
{
ll x,y,z;
friend bool operator<(node a,node b){return a.z>b.z;}
};
priority_queue<node>que;
struct line
{
double k,b;
line(){}
line(double kk,double bb){k=kk,b=bb;}
}stack[MAXN];
double cor[MAXN];
__attribute__((optimize("-O3")))
inline ll read()
{
ll x=0,f=1;char ch=getchar();
if (ch=='x')return 0;
while (ch<'0' || '9'<ch){if (ch=='-')f=-1;ch=getchar();}
while ('0'<=ch && ch<='9')x=x*10+ch-'0',ch=getchar();
return x*f;
}
__attribute__((optimize("-O3")))
inline void link(ll x,ll y,ll z)
{
next[++tot]=last[x],last[x]=tot,tov[tot]=y,len[tot]=z;
}
__attribute__((optimize("-O3")))
inline void dijkstra()
{
memset(f,64,sizeof(f));
que.push((node){S,0,0}),f[S][0]=0;
while (!que.empty())
{
node now=que.top();que.pop();
ll x=now.x,y=now.y,z=now.z;
if (z>f[x][y])continue;
rep(i,x)if (!len[i])
{
if (y==n)continue;
node tmp={tov[i],y+1,z};
if (f[x][y]<f[tov[i]][y+1])
{
f[tov[i]][y+1]=f[x][y];
que.push(tmp);
}
}
else
{
node tmp={tov[i],y,z+len[i]};
if (f[x][y]+len[i]<f[tov[i]][y])
{
f[tov[i]][y]=f[x][y]+len[i];
que.push(tmp);
}
}
}
}
__attribute__((optimize("-O3")))
inline double get(double k1,double b1,double k2,double b2)
{
return (b2-b1)/(k1-k2);
}
__attribute__((optimize("-O3")))
int main()
{
freopen("T3.in","r",stdin);
n=read(),m=read();
fo(i,1,m)
{
ll x=read(),y=read(),z=read();
link(x,y,z);
}
q=read();
while (q--)
{
S=read(),T=read(),dijkstra();bool flag=1;
fo(i,0,n)if (f[T][i]<INF){flag=0;break;}
if (flag){printf("0 0\n");continue;}
if (f[T][0]>INF){printf("inf\n");continue;}
ll top=0,sum=0;
fd(i,n,0)
{
if (f[T][i]==INF)continue;
while (top && get(stack[top].k,stack[top].b,i,f[T][i])<=cor[top])--top;
stack[++top]=line(i,f[T][i]);
if (top>1)cor[top]=get(stack[top-1].k,stack[top-1].b,stack[top].k,stack[top].b);
}
fo(i,1,top-1)
{
ll l=(ll)cor[i],r=(ll)cor[i+1];
if (l<r)sum+=(l+r+1)*(r-l)/2*stack[i].k+stack[i].b*(r-l);
}
ll num=(ll)cor[top];
if (cor[top]!=num || top==1)++num,sum+=f[T][0];
printf("%lld %lld\n",num,sum);
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号