并查集详解

　　最近回顾了一下最小生成树，发现以前学的太浅了。。。没有仔细分析其中的每一步，汗颜。。发现Kruskal算法可以用到并查集的东西，就把并查集重新温习了一下。注：这里有部分内容来自网络，有部分内容在算法导论（第二版21章）中也有。

　 　并查集

      并查集是一种树形结构，又叫“不相交集合”，保持了一组不相交的动态集合，每个集合通过一个代表来识别，代表即集合中的某个成员，通常选择根做这个代表。

　　三种主要操作：

Make_Set(x):

建立一个新的集合，其唯一成员就是x，因此这个集合的代表也是x，并查集要求各集合是不相交的，因此要求x没有在其他集合中出现过。

Find_Set(x):

返回能代表x所在集合的节点，通常返回x所在集合的根节点。有递归和非递归两种方法，下面会有讲解。

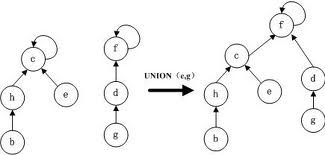
Union(x, y):

将包含x,y的动态集合合并为一个新的集合。合并两个集合的关键是找到两个集合的根节点，如果两个根节点相同则不用合并；如果不同，则需要合并。

                     

并查集的优化：

Union(x, y)时按秩合并：

合并时，如果两个集合的秩相同，任选一个根做为父节点，并增加其秩。

秩不同时，让较小秩的集合指向较大秩的集合，这时秩的大小不变。

秩和集合的数目是不一样的，秩表示节点高度的一个商界；集合的数目表示集合中节点的总数。

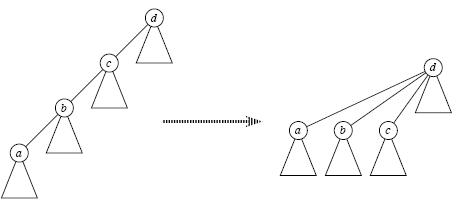
Find_Set(x)路径压缩：

在Find_Set(x)中，是查找路径上的每个节点都直接指向根节点，这样下次再找根节点的时间复杂度会变成o(1)

 

主要代码：

 

//建立一个新的集合，每一个子节点就是一个数，本身就是他的根节点
void Make_Set(int x)
{
    father[x] = x;
    R[x] = 0;
}

//通过递归向上查找根节点，回溯时改变当前节点的父节点，直接指向根节点。
int Find_Set(int x)
{
    if(x != father[x])
        father[x] = Find_set(father[x]);
    return father[x];

}

//将根节点设置为-1的非递归方法
int Find_Set2(int x)
{
    int y = x;
    while(y!= -1)
        y = father[y];
    return y;
}

//两个集合的合并算法
void Union(int x, int y)
{
    int GrandX = Find_set(x);
    int GrandY = Find_set(y);

    if(GrandX == GrandY)
        return;
    if(R[GrandX] < R[GrandY])
        father[GrandX] = GrandY;
    else
    {
        if(R[GrandX] == R[GrandY])
            R[GrandX]++;
        father[GrandY] = GrandX;    
    }
}

本文学习借助了勇幸的博客，感谢，这里注明链接：http://www.ahathinking.com/