RNN & LSTM详解
1.1 RNN概述
RNN很多实施情况都可通过时间序列模型来描述（RNN又被叫做序列模型）。
例如，如果你想写一个文档，单词的顺序很重要，当前的单词肯定取决于以前的单词。如果把注意力放在文字写作上…… 一个单词中的下一个字符取决于之前的字符（例如，The quick brown f...，下一个字母是 o 的概率很高），如下图所示，关键思想是在给定上下文的情况下产生下一个字符的分布，然后从分布中取样产生下一个候选字符：
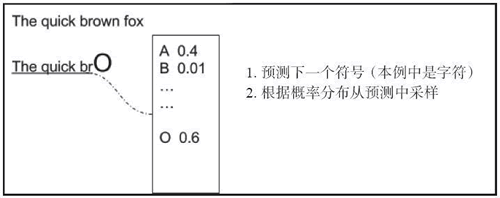
一个简单的变体是存储多个预测值，并创建一个预测扩展树，如下图所示：
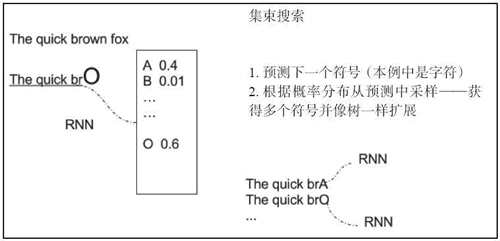
基于序列的模型可以用在很多领域中。在音乐中，一首曲子的下一个音符肯定取决于前面的音符，而在视频领域，电影中的下一帧肯定与先前的帧有关。此外，在某些情况下，视频的当前帧、单词、字符或音符不仅仅取决于过去的信号，而且还取决于未来的信号。
1.2 RNN基本模型介绍
基于时间序列的模型可以用RNN来描述，其中，时刻 i 输入为 Xi，输出为 Yi，时刻 [0，i-1] 区间的状态信息被反馈至网络。这种反馈过去状态的思想被循环描述出来，如下图所示：
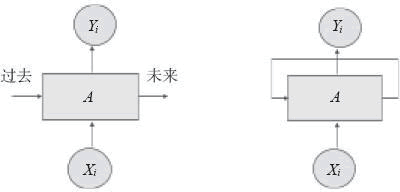
展开（unfolding）网络可以更清晰地表达循环关系，如下图所示：
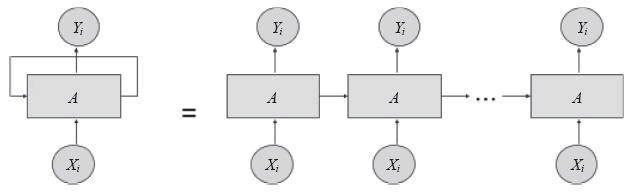
而RNN模型通过区别隐层接收的是上一时刻的隐层还是上一时刻的输出将其分为两种基础模型结构：
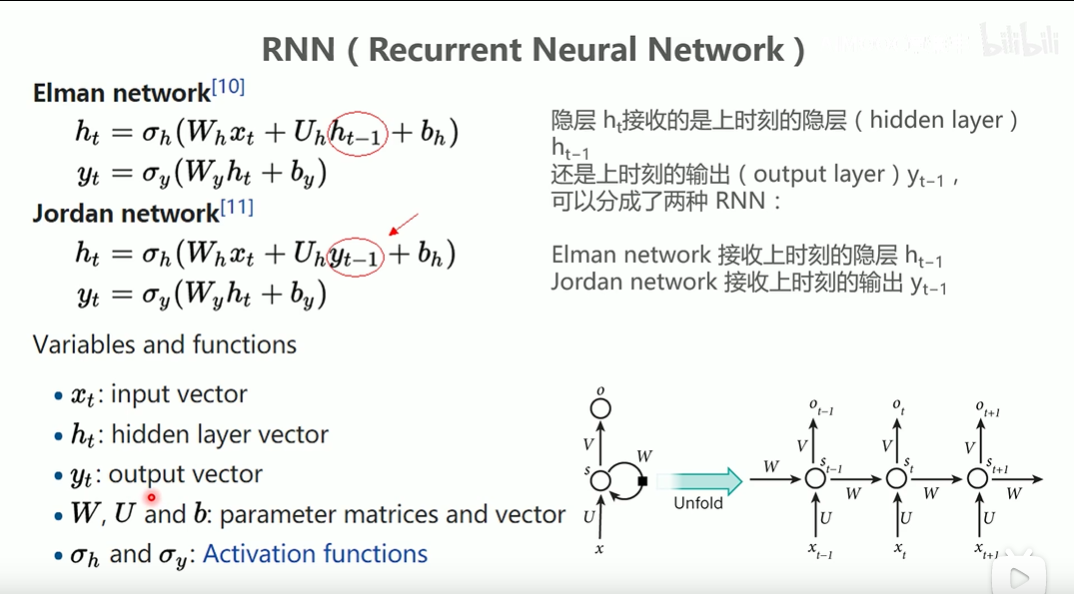
最简单的 RNN 单元由简单的 tanh 函数组成，即双曲正切函数，如下图所示：
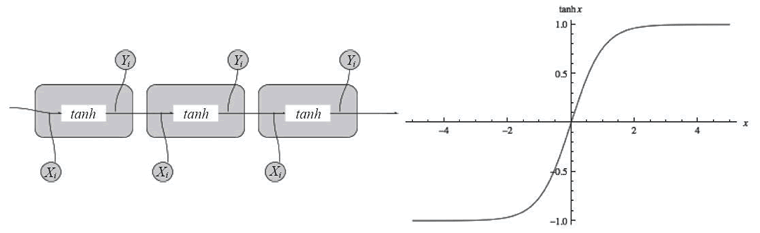
1.3 双向RNN（Bidirectional RNN）
RNN既然能继承历史信息，是不是也能吸收点未来的信息呢？因为在序列信号分析中，如果我能预知未来，对识别一定也是有所帮助的。因此就有了双向RNN、双向LSTM，同时利用历史和未来的信息。
双向RNN
值得一提的是，但由于RNN 建模中的遗忘性，最后一个 state 中包含的信息是有损的，且序列越靠前的信息损失可能越严重。一种比较可行的解决方法是同时训练两个RNN，一个正向学习，一个反向学习，将正向的和反向的最后一个state 对应向量 concate 后得到的向量作为最终产物。
对于正向RNN最后一个向量中记录的信息量从前往后依次增强，反向的最后一个state记录的信息从后往前依次增强，两者组合正好记录了比较完整的信息。
1.4 RNN的多种结构（处理向量序列）
RNN 强大的是它能够处理向量序列，其中 RNN 的输入和输出可以是序列，下图很好地说明了这一点，最左边的例子是一个传统（非递归）网络，后面跟着一个序列输出的 RNN，接着跟着一个序列输入的 RNN，其次跟着序列输入和序列输出不同步的 RNN，最后是序列输入和序列输出同步的 RNN。
RNN序列示例图：
机器翻译是输入序列和输出序列中不同步的一个例子：网络将输入文本作为一个序列读取，读完全文后输出目标语言。
视频分类是输入序列和输出序列同步的一个例子：视频输入是一系列帧，对于每一帧，在输出中提供分类标签。
详解见：https://www.jiqizhixin.com/articles/2018-12-14-4
2、RNN所涉及的梯度问题
由于存在两个稳定性问题，训练 RNN 是很困难的。由于反馈环路的缘故，梯度可以很快地发散到无穷大，或者迅速变为 0。如下图所示：
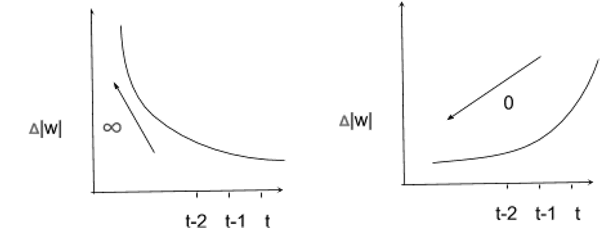
在这两种情况下，网络将停止学习任何有用的东西。梯度爆炸的问题可以通过一个简单的策略来解决，就是梯度裁剪。梯度消失的问题则难以解决，它涉及更复杂的 RNN 基本单元（例如长短时记忆（LSTM）网络或门控循环单元（GRU））的定义。先来讨论梯度爆炸和梯度裁剪。
梯度裁剪包括对梯度限定最大值，以使其不能无界增长。如下图所示，该方法提供了一个解决梯度爆炸问题的简单方案：
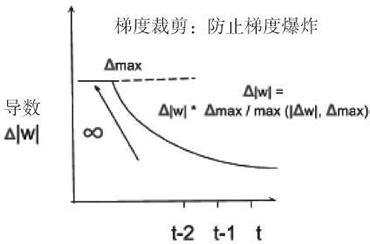
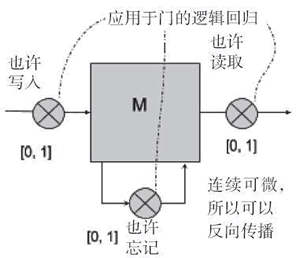
解决梯度消失需要一个更复杂的记忆模型，它可以有选择地忘记以前的状态，只记住真正重要的状态。如下图所示，将输入以概率 p∈[0，1] 写入记忆块 M，并乘以输入的权重。以类似的方式，以概率 p∈[0，1] 读取输出，并乘以输出的权重。再用一个概率来决定要记住或忘记什么：
3、长短时记忆网络（LSTM）
长短时记忆网络可以控制何时让输入进入神经元，何时记住之前时序中学到的东西，以及何时让输出传递到下一个时间戳。所有这些决策仅仅基于输入就能自我调整。乍一看，LSTM 看起来很难理解，但事实并非如此。我们用下图来解释它是如何工作的：
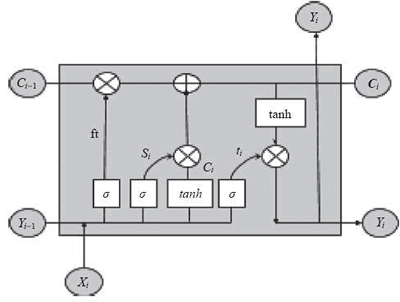
首先，需要一个逻辑函数 σ 计算出介于 0 和 1 之间的值，并且控制哪个信息片段流经 LSTM 门。请记住，logisitic 函数是可微的，所以它允许反向传播。
然后需要一个运算符 ⊗ 对两个相同维数的矩阵进行点乘产生一个新矩阵，其中新矩阵的第 ij 个元素是两个原始矩阵第 ij 个元素的乘积。同样，需要一个运算符 ⊕ 将两个相同维数的矩阵相加，其中新矩阵的第 ij 个元素是两个原始矩阵第 ij 个元素的和。在这些基本模块中，将 i 时刻的输入 xi 与前一步的输出 yi 放在一起。
方程 fi = σ(Wf · [yi - 1, xi] + bf) 是逻辑回归函数，通过控制激活门 ⊗ 决定前一个单元状态 Ci-1 中有多少信息应该传输给下一个单元状态 Ci（Wf 是权重矩阵，bf 是偏置）。逻辑输出 1 意味着完全保留先前单元状态 Ct-1，输出 0 代表完全忘记 Ci-1 ，输出（0，1）中的数值则代表要传递的信息量。
接着，方程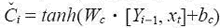
根据当前输入产生新信息，方程 si = σ(Wc · [Yi - 1, Xi] + bc) 则能控制有多少新信息
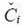通过运算符 ⊕ 被加入到单元状态 Ci 中。利用运算符 ⊗ 和 ⊕，给出公式
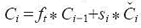对单元状态进行更新。
最后，需要确定当前单元状态的哪些信息输出到 Yi。很简单，再次采用逻辑回归方程，通过 ⊗ 运算符控制候选值的哪一部分应该输出。在这里有一点需要注意，单元状态是通过 tanh 函数压缩到 [-1，1]。这部分对应的方程是 Yi=ti * tanh(Ci)。
LSTM的理论讲解看上去好像十分复杂，但它的运用其实非常简单。你可以使用LSTM单元作为标准RNN元的黑盒替换，即可解决梯度消失问题。而大多数深度学习框架提供了相关内容的调用。
4、门控循环单元（GRU）和窥孔LSTM
近年来已经提出了许多 LSTM 的变种模型，其中有两个很受欢迎：窥孔（peephole）LSTM 允许门层查看单元状态，如下图中虚线所示；而门控循环单元（GRU）将隐藏状态和单元状态合并为一个信息通道。
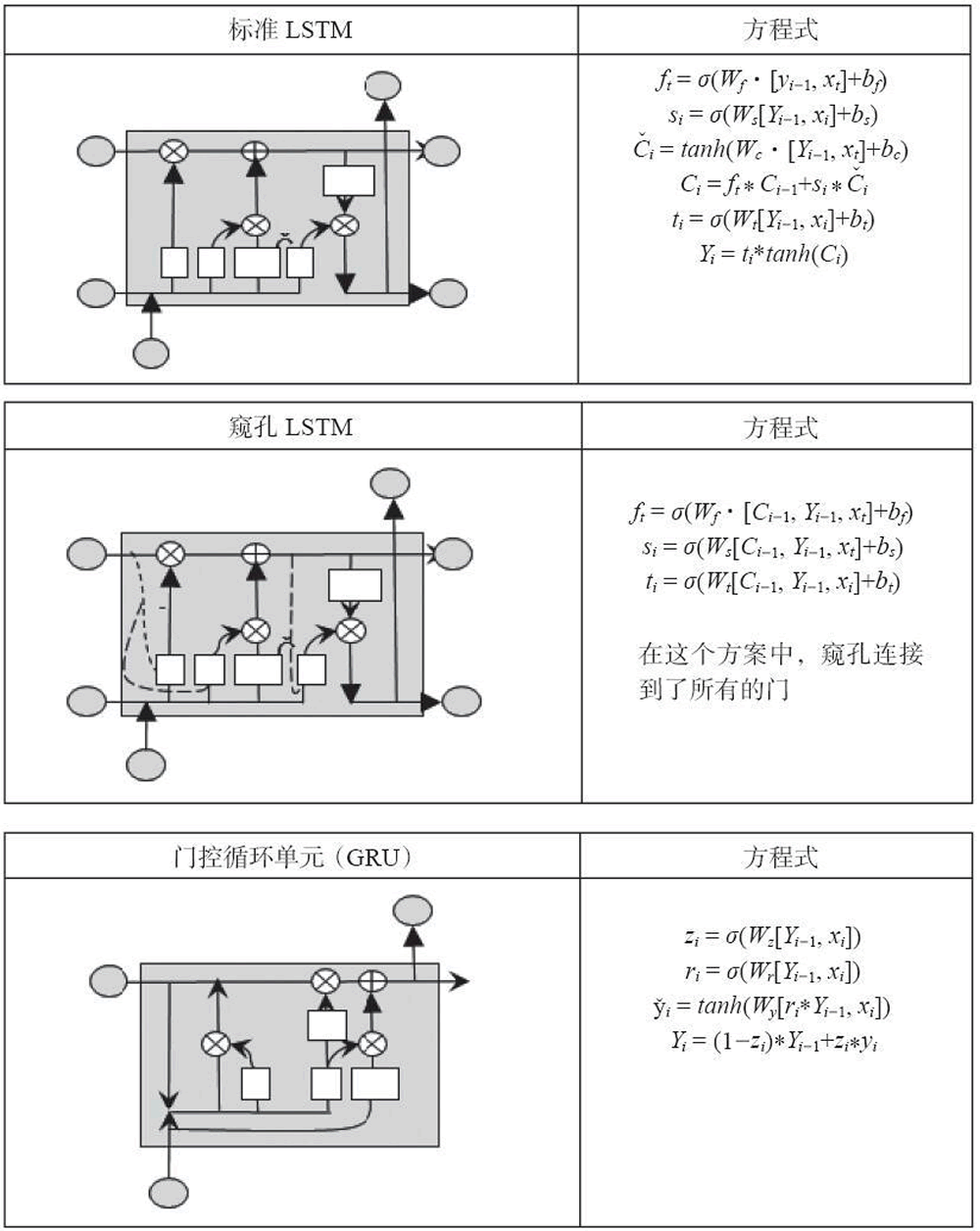
GRU单元是LSTM单元的简化版，性能相似。主要简化如下：
- 长期状态和短期状态合并为一个单独的向量。
- 采用单独的门控来控制遗忘门和输入门。如果门控输出1，输入门打开，遗忘门关闭。如果门控输出0，执行相反的操作。当一些记忆需要存储时，存储这些信息的地方需要先清空。这实际上是LSTM单元及其自身的常见变体。
- 没有输出门，每个时间节点输出全部状态向量。然而，新引入一个控制器来控制前一个状态的哪个部分提供给主层。
参考资料
简书 - 循环神经网络（RNN） 基础讲解：https://www.jianshu.com/p/9f155515bdf0
C语言中文网 - RNN循环神经网络及原理（详解版）：http://c.biancheng.net/view/1946.html
Bilibili - RNN介绍（覃秉丰Pytorch课程）：https://www.bilibili.com/video/BV1iv41117Zg?p=25
知乎 - 循环神经网络（RNN）笔记——LSTM：
