2023算法笔记
Hoppz算法笔记
前言
2023_02_18还是太菜了,笔记基于
《算法导论》 && 《数据结构与算法分析 C++描述》 && 《C++ Primer 》&& 《算法进阶指南》 && 《OI_Wiki》&& [cppreference.com],想着为复试准备(虽然很大程度上今年是考不上了),就开始重看算法导论,前几年大致翻过几页,感觉数学证明太多直接放弃了,想着学了一点微积分,线代,概率论的知识(虽然学的不好,但总是有点基础了)就又开始看了。本文部分代码采用new Bing编写。
1、基础知识
1.1、排序算法
1.1.1、插入排序(insertionsort)
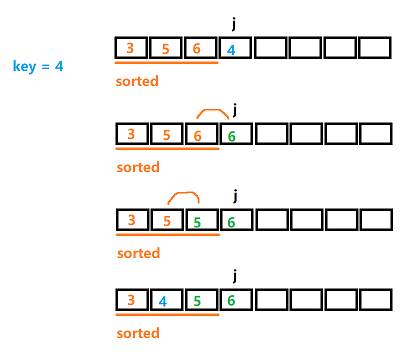
插入排序与我们整理扑克牌类似。
开始时,我们左手为空并且桌子上的牌面向下(意思就是我们并不会在意牌出现的顺序)。然后,我们每次从桌子上拿走一张牌并将它插入左手正确的位置。
《算法导论》p10
插入排序有两个过程:
- 将
a[j-1]的值移动到a[j],这样a[j-1]的位置就空出来了 (便于插入) - 重复 1 直到
key的位置被空出来,再把key插入到这个位置。
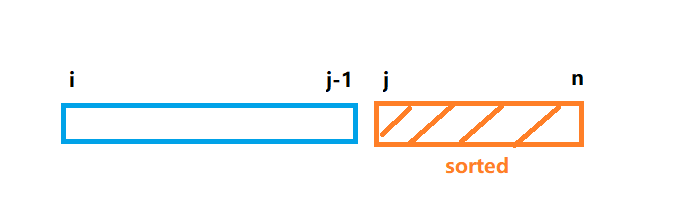
插入排序由 趟排序组成。对于 到 趟,插入排序保证从位置 到位置 上的元素为已排序状态。插入排序利用了这样的事实:已知位置 到位置 上的元素已经处于排过序的状态(上图表示为 sorted 数组 )。
(sorted 数组就相当于已整理好的手牌,蓝色部分为 unsorted 就如桌子上没整理的扑克牌。我们每遍历到一个新的 j ,就相当于从桌面拿一个新的手牌,然后从右向左依次与此手牌的值比较,找到合适的位置插入)
可能在上面的过程 1 有点抽象,其原理是非常简单的,为什么要将a[j-1] 的值移动到 a[j]?
他的原理就和匹配手牌一样,大于 key 的值就向后移动,为插入的值腾出空间。在第三行中出现了两个 ,第一个 的位置可以看成是空的,就是待插入的位置。
最后一个
a[j+1] = x,为什么j需要加一?(这个问题很重要)
注意 while 的后面不能写成 a[j+1] = a[j--]; 可能会出现 bug
1.1.1.1、插入排序与逆序数
逆序数
成员为数的数组的一个 逆序 即具有性质 但 的序列。即位置大,数值小,或者说位置小数值大都是可以的。
在序列 {34,8,64,51,32,21} 中有 个逆序,即(34,8),(34,32),(34,21),(64,51),(64,32),(64,21),(51,32),(51,21),(32,21)。值得注意的是,这正好是需要由插入排序执行的交换次数。因为交换两个不按顺序排列的相邻元素恰好消除一个逆序,而一个排过序的数组没有逆序。由于算法中还有 项其他的工作,因此插入排序的运行时间是 ,其中 为原始数组中的逆序数。于是,若逆序数是 ,则插入排序以线性时间运行。
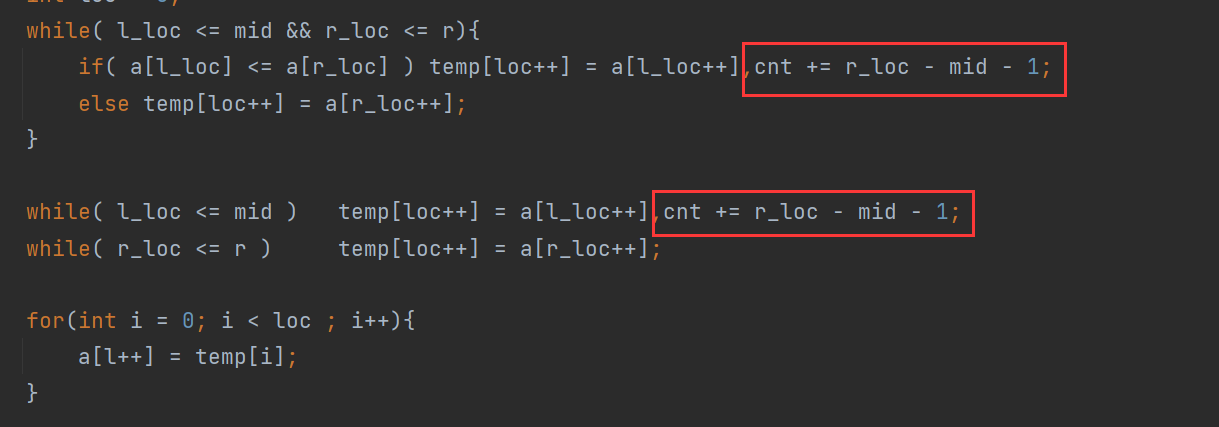
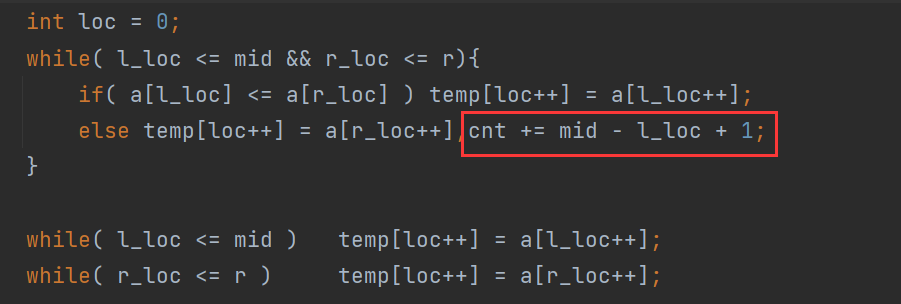
cnt 为逆序数。代码仅在比较重添加了一行。
1.1.2、冒泡排序
在插入排序(Ascend版本)中 unsorted 数组中的 key 会与 sorted 数组中的数字交换,找到它在 sorted 数组中的正确位置。
冒泡排序则是把unsorted 数组中的最大值交换到 j-1 的位置,之后 形成新的 sorted 数组。
每一轮的开始指针都指向 的位置,如果左边的值大于右边的值那么就交换两个相邻的元素,然后移动指针到下一位,第一轮的结束位置为 ,第二轮的结束位置为 ,直到最后一轮的结束位置为 。
算法保证,第一轮最大值一定会移动到数组的末尾,第二轮次大值一定为移动到倒数第二个位置···,一直循环 n-1 次,最后一次最小值一定在第一个位置,不用移动。
这种每轮把最大值通过交换的方式移动到数组末尾的方式,就像气泡不断向上浮动,所以叫做冒泡排序
1.1.2.1、冒泡排序与逆序数
与插入排序相同冒泡排序也是基于交换的排序算法, 与 满足 就会产生一次交换,这是符合逆序数的定义的。可以证明总的交换次数,就是逆序对的数量。
cnt 为逆序数的数量。
1.1.3、选择排序(selectionsort)
选择排序和冒泡排序都会在每一轮结束时把当前 unsorted 的数组中的最大值移动到 sorted 的左端。不一样的是选择排序不会在比较的过程中直接交换,而是通过记录当前最大值的下标的方式,在比较完所有未排序的数之后直接交换最后一个位置与最大的位置。
1.1.4、希尔排序
希尔排序可以看做是插入排序的升级版,核心思想是与插入排序一致的。引入增量这一概念,通过比较相距一定间隔(增量)的元素来工作 ,直到只比较增量为 的最后一趟排序为止。在这个过程中增量会逐轮递减,由于这个原因,希尔排序有时也叫做 缩减增量排序(diminishing increment sort)。
在使用增量 gap 的一趟排序之后,对于每一个 都有 ,同时 (如果下标都在合法范围内的话)。这样对于所有间隔 所组成的序列,都是有序的(如下图的 {81,35,41})。
增量序列一个流行(但是不好)的选择是使用 Shell (算法提出者)建议的序列: 二的幂次方。
下面的实现可以与之前的插入排序做比较,可以发现只是多了一层对于 的循环,核心代码和插入排序完全一致,把 -1,+1 操作换成了 -gap,+gap 操作。
1.1.5、归并排序(megersort)
许多有用的算法在结构上是递归的:为了解决一个 给定的问题,算法一次或多次递归地调用其自身以解决紧密相关的若干子问题。
这些算法典型地遵循分治的思想:
将原问题分解为几个规模较小但类似于原问题的子问题,递归的求解这些子问题,然后再合并这些子问题的解来建立原问题的解。
分治模式在每层递归时都有三个步骤:
- 分解原问题为若干子问题,这些子问题都是原问题的规模较小的实例。
- 解决这些子问题,递归地求解各子问题。然而,若子问题的规模足够小,则直接求解。
- 合并这些子问题的解成原问题的解。
归并排序算法完全遵循分治模式。直观上其操作如下:
- 分解:分解待排序的 个元素的序列成各具 个元素的两个子序列
- 解决:使用归并排序递归的排序两个序列
- 合并:合并两个已排序的子序列以产生排序答案
当排序的序列长度为1时,递归
开始回升,在这种情况下不需进行任何操作,因为长度为 的每个序列都已排好序。
详细操作见 《算法导论》-p17
带哨兵的merge
注意: 使用 vector 初始化第一个迭代器不用 +1 ,后面一个迭代器要 +1
不带哨兵的 merge
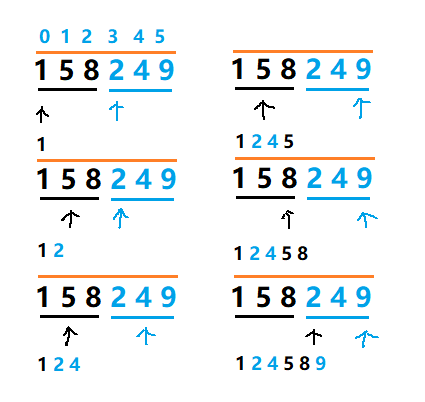
归并排序关键在于它的 merge 函数,核心思想是深刻而简单的,我们以不带哨兵的版本为例。
两个指针分别指向划分的两个区间,第一个区间[l,mid] ,第二个区间为 [mid+1,r]。我们用两个指针指向两个区间的前端,然后不断的比较两个指针直线的值的大小。再借助一个辅助数组 te,每次比较中,较小的值存入 te 移动相应的指针,重复这一过程,完成归并。
2.1.2.1、归并排序解决逆序对问题
假设 是一个有 个不同数的数组。若 且 ,则对偶 称为 的一个 逆序对
-
由集合 构成的什么数组具有最多逆序对?
- 降序排列的数组具有最多的逆序对,共 对。
-
插入排序的运行时间与输入数组中逆序对的数量之间是什么关系?
- 插入排序的主要思想讲数组分为 sorted 数组和 unsorted 数组,当我们处理到
j元素时while循环中 与 交换的次数即为逆序对的数量
- 插入排序的主要思想讲数组分为 sorted 数组和 unsorted 数组,当我们处理到
-
使用归并排序来处理逆序对问题
值得注意的是插入排序,冒泡排序的交换次数也是原数组的逆序对数量
1.1.6、堆排序(heapsort)
与归并排序一样,但不同于插入排序的是,堆排序的时间复杂度是 。
而与插入排序一样,但不同于归并排序的是,堆排序同样具有原址空间性:任何时候都只需要常数个额外的元素空间储存临时的数据。因此,堆排序是集合了我们前面两种排序算法优点的一种排序算法。
下面是二叉堆最重要的两个性质:
-
(二叉)堆是一个数组,可以被看成一个近似的完全二叉树。
-
二叉堆可以分为两种形式:最大堆和最小堆
最大堆:除了根节点都要满足
最小堆:除了根节点都要满足
在堆排序中,我们使用的最大堆与最小堆,也可用于构造优先队列。
我们可用用自底向上的方法利用过程 Max_Heapify 把一个大小为 n 的数组转换为堆。
我们可以证明子数组
A[ n>>1,n ]中的元素都是叶子节点,不用Heapify这个过程,所以我们只用调用非叶子节点,从后向前的进行Heapify。
注意:max_heapify 函数中,不要忘了l_son<=heap_size 要判断这种情况。
1.1.6.1、最大优先队列
1.1.6.2、最小优先队列
1.1.7、快速排序(quicksort)
与归并排序一样,快速排序也使用了分治的思想。下面是一个快速排序的最普通的实现——经典快速排序 ,此时的输入是一个数组。
我们先从一个简单的角度出发。随意取数组中的一项(我们记为 ),把数组划分成三个部分。
- 值小于 的部分;
- 值等于 的部分;
- 值大于 的部分。
递归的对第 1 组以及第 3 组进行排序,然后再把这三个组合并。下述为实现代码
我们可以发现这个算法和归并排序是很类似的,都使用了分治的思想。为了更好的运行效率,以及避免使用大量的内存,这样的快速排序一般避免创建第二个数组(相等的项)的方式编写。这种写法有多出影响算法性能的精妙细节,一些难点也都在这里。
将数组 S 排序的经典快速排序算法由下列简单的 步组成。
- 如果 中的元素是 或 则返回。
- 取 中任一元素 ,称为隔板。
- 将 划分成两个不相交集合:,。
- 返回 。
对于不同的隔板选择,会使得第三步对分割的描述不是唯一的,因此这就成了一种设计决策。一部分好的实现方法是将这种情形尽可能高效地处理。直观地看,我们希望把等于隔板值的一半的元素划分给 ,而另一半划分到 ,这很像我们希望二叉查找树左右的节点个数相同的情形。
1.1.7.1、隔板的选择
这里讨论的是 2 中的具体实现。
虽然上述算法无论选择那个元素作为隔板都能完成排序工作,但是有些选择显然优于其他的选择。
最常见的一种错误就是选择将第一或最后一个元素作为隔板,因为这样对于一个有序数组,或者一个所有值都相同的数组,那么快速排序的时间复杂度将会退化为 。在算法导论中的第一个算法的缺陷就是如此。
这里的
x = A[r]就直接认定当前区间的最后一个元素的值作为隔板的值。
一种安全的方式是随机选择隔板值,但是随机数的生成一般来说开销显著,根本减少不了算法其余部分的平均运行时间。
一种被验证高效且安全的方式是 三数中值分割法 ,就是我们常用的取数组中间的那个数作为隔板值。使用三数中值分割法消除了预排序输入的坏情况,并且实际减少了 的比较次数。具体实现代码如下
这种选择使得最后将会满足 。
通常来说,我们直接取 a[mid] 作为隔板值就好了。
1.1.7.2、分割策略
这里讨论的是 3 中的具体实现。
在确定了隔板值之后,我们用两个指针指向 l-1 以及 r+1 处。在分割阶段要做的就是将所有小元素移动到数组的左边,将所有大的元素移动到数组的右边。当然,小和大都是相对于隔板值而言的。
当 i 在 j 的左边的时候,我们不断将 i 向右移动,略过那些小于隔板值的元素;同样我们不断将 j 向左移动,略过那些大于隔板值的元素。如果 i 遇到了大于或等于 隔板值的元素则停止, j 遇到了 小于或等于 隔板值的元素则停止。
当 i 和 j 都停止时,a[i] 满足 (val就是隔板值),a[j] 满足 ,这种情况下对 a[i] 和 a[j] 进行交换维护我们之前的集合划分。其效果就是将一个大的元素移到右边,将一个小的数移到左边。
重复上述的步骤直到 i>= j 。
在这样的交换全部完成后,能保证 $a[l,j]\le val a[j+1,r] \ge val$ ,所以我们继续递归的对这两个区间继续排序。
如果是从 的角度出发那么区间划分是: ,,但在 , 的初始化的情况下会出现 的情况。如果要返回这个区间的话,就需要对这种情况特判一下:
如果还不理解建议手推一遍。
下面代码采用的是思考
《算法导论》7-1的Hoare划分
1.1.7.4、小数组
对于很小的数组 ,快速排序不如插入排序好。不仅如此,因为快速排序是递归的,所以这样的情形还经常发生。通常的解决方法是对于小的数组不递归地使用快速排序,而代之以诸如插入排序这样的对小数组有效的排序算法。
完整代码:
1.1.7.5、小结
快速排序的核心思想是在一段待排序的数组中选择一个数,以此数为基础将数字划分为三个集合,分别为小于这个数的集合,等于这个数的集合,大于这个数的集合。再依次将这三个集合按序放置,形成新的数组,再递归的处理第一个和最后一个数组,从而使得整个数组有序。
以之前的 sorted 与 unsorted 划分的话,每一次递归会使等于这个数的集合中的所有数落到正确的位置。(橙色为 sortd ,蓝色为 unsorted,下文的隔板选择为集合中间元素,即 )
然而这样的划分还有可以优化的部分,我们采取一种经验验证更好的划分方式,这种划分可以把第二个集合的数,较为平均的分散到第一个和最后一个集合中。这样划分就会丢失隔板位置的确定性(影响下文的快速选择算法),但会使得代码在排序方面更有效率。
1.1.7.6、快速选择排序
相当于
nth_elment()在 的时间内返回这个数组第 小的数
quick_selection()中的递归边界非常重要!!
快速选择算法步骤与快速排序类似,如下:
- 选择一个隔板
- 将集合 分割为 与 ,就和快速排序中一样。
- 如果 ,那么第 小的数一定在 中。在这种情况下返回
quick_selection(S1,k)。
如果 ,那么第 小的数一定在 中。在这种情况下返回quick_selection(S2,k - |S1|-1)。 - 集合的大小会不断的收缩,当收缩到 的时候,最后留下的那个元素就是我们要找的值。
我们采取的
partition方式,并不能使长度大于 的集合中某元素的位置是最终的位置,因为满足的性质为,。最初的三个部分的分割,第二个部分一旦确定就肯定是最终的位置,但对于这种二元分割就必须要递归到集合长度为 才能最终确定该数的位置为最终位置。
1.1.8、计数排序(countsort)
计数:记录比数小的数有多少个
计数排序的基本思想是:
对每一个输入元素 ,确定小于 的元素的个数。
利用这一信息,就可以直接 放到它在输出数组中的位置上了。当有几个元素相同时u,这一方案要略做修改。
我们需要首先给出当前数组的最大值以及数组的大小,还需要两个辅助数组。
1.1.9、基数排序
1.1.10、桶排序
1.1.11、排序后记
插入排序、归并排序、堆排序及快速排序都是比较排序算法:它们都是通过对元素进行比较操作来确定输入数组的有序次序。
我们可以证明任意比较排序算法排序 个元素的最坏情况运行时间的下界为 ,从而证明堆排序和归并排序是渐近最优的比较排序算法。
1.3、贪心算法
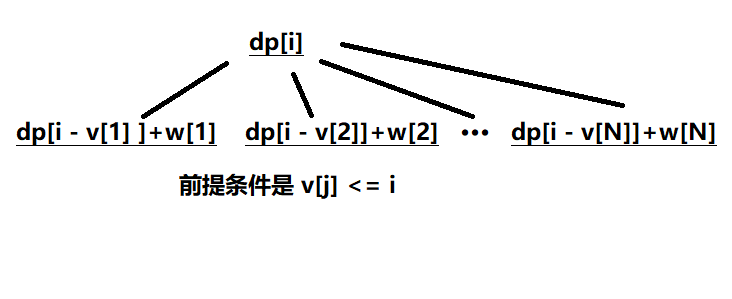
求解最优化问题的算法通常需要经过一些列的步骤,在每个步骤都面临多种选择。对于许多最优化问题,使用动态规划算法来求最优解有些杀鸡用牛刀了,可以使用更简单、更高效的算法。
贪心算法就是这样的算法,它在每一步都做出当时看起来最佳的选择。也就是说,它总是做出局部最优的选择,寄希望这样的选择能导致全局最优解。
将一个问题划分为若干类,如果可以证明答案在某一个或几个类中,则为贪心算法。如果无法证明,答案可以在所有的类中,那么就是 DP(动态规划)。
1.3.1、活动选择问题
我们的第一个例子是调度竞争共享资源的多个活动的问题,目标是选出一个最大的互相兼容的活动集合。
假定有一个 个活动的集合 ,这些活动使用同一个资源(例如一个教室),而这个资源在某个时刻只能供一个活动使用。每个活动 都有一个开始时间 与一个结束时间 。如果被选中,任务 发生在半开时间区间 期间。如果两个活动 和 满足 和 不重叠,则称他们是兼容的。在活动选择问题中,我们希望选出一个最大兼容活动集。
对于最优子结构的构造,类似于最长上升子序列的思路
1.5、搜索算法
1.5.1、折半搜索(二分)
二分的基础的用法是在单调序列或单调函数中进行查找。因此当问题的答案具有单调性时,就可以通过二分把求解转化为判定。
1.5.1.1、标准二分
标准的二分搜索,数组中没有重复元素,如果没有这个数则返回
-1
我们先来分析搜索的值都是唯一的。
{1,2,5,8,9,10} 对应的下标从 0 开始,我们执行 binarySearch1(vec,8)
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 5 | 2 | 5 < key(8) | l = mid + 1 = 3 |
| 2 | 3 | 5 | 4 | 9 > key(8) | r= mid - 1 = 3 |
| 3 | 3 | 3 | 3 | 8 == key | return mid |
-
我们要找的值为
key如果a[mid] < key那么在区间a[l,mid]内都不可能存在==key的值了(单调性),所以我们将l = mid +1而不是l = mid因为a[mid]这个值肯定不在我们的解空间内。对于r = mid - 1也是相同的道理。 -
对于
while中的条件,我们可以发现我们是在最后一轮中得到的key == a[mid]所以我们需要l==r这个情况,这样写的好处就是,如果没有这个数的话直接就返回-1了,不用再写个特判。
现在我们来考虑当数组搜索的值不唯一的情况。
数组变成了 {1,2,2,4,4,4,7,7,8} ,下标也是从 0 开始,我们先执行 binarySearch1(vec,4)
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 8 | 4 | 4 | return 4 |
再执行 binarySearch(vec,7)
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 8 | 4 | 4 < key(7) | l = mid + 1 = 5 |
| 2 | 5 | 8 | 6 | 7==key | return 6 |
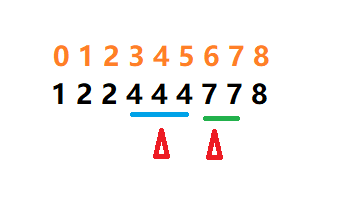
通过这两次的数据,我们可以发现,对于 binarySearch1 搜索的值出现过多次的情况下,返回的位置是不确定的。现在我们要做的事情就是让这个值确定下来,有两种优化的思路,第一个就是返回相同数中下标最小的位置,另一个为返回相同数中下标最大的位置。
1.5.1.2、返回最小下标
一个简单的思路是,只用修改 if( a[mid] == key ) 中的代码,不直接返回,而是向左遍历,直到右边不等于 key 时
这个代码有个很明显的缺点,当数组中所有数都相同的话,算法的时间复杂度会退化到 ,这显然不是我们想看到的情况。
我们回到 binarySearch1(vec,4) 中
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 8 | 4 | 4 | return 4 |
在第一次的折半后 a[mid]值等于 key 值,那么 mid 值是可能成为返回的位置的,但是在 [mid+1,r] 即便有 ==key 的情况,但也不是我们想要的答案了(我们想要的是下标最小的位置),所以我们改动 if(a[mid==key]) 得到 binarySearch2
执行 binarySearch2(vec,4)
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 8 | 4 | 4 == key(4) | r = mid |
| 2 | 0 | 4 | 2 | 2 < key(4) | l = mid + 1= 3 |
| 3 | 3 | 4 | 3 | 4 == key(4) | r = mid = 3 |
| 4 | 3 | 3 | return 3 |
值得注意的是这里的 while 中的条件就没有等于了,也就是说当 l==r 时,就已经定位到答案了。
还有一点,如果搜索的数不存在的话,将会返回比
key小的数中最大的数,且如果这个数有多个的话,返回位置最大的那个。
1.5.1.3、返回最大下标
这就和刚才的思路是完全一样的这里就不过多赘述了直接上代码
然后在编写代码的时候就出 bug 了。如果我们直接改的话,代码是这样的
执行 binarySearch3(vec,4)
| 轮数 | l | r | mid | a[mid] | 变化 |
|---|---|---|---|---|---|
| 1 | 0 | 8 | 4 | 4 == key(4) | l = mid = 4 |
| 2 | 4 | 8 | 6 | 7 < key(4) | r = mid - 1 = 5 |
| 3 | 4 | 5 | 4 | 4 == key(4) | l = mid |
| 4 | 4 | 5 | ... | 后面就死循环了 |
我们想要的是一直向右在,因为在向左走时, (l+r)/2 会自动向下取整!!,之前在分析的时候就忽略了这个,所以还要改动 mid 最终的代码:
在这里如果有相同的数将会返回最右边的数,如果不存在的话返回第一个比它大的数,如果有多个的话,返回下标最小的那个
前面两种情况讨论的是如果存在多个相同的数,我们应该如何控制边界的情况,我们主要修改的地方在a[mid] == key 。下面还有一种没有讨论的情况,就是当要查找的数不存在的时候,
在单调序列 a 中查找 的数中最小的一个。 最大化最小值
在单调序列 a 中查找 的数中最大的一个。最小化最大值
1.6、递推与递归
一个实际问题的各种问题可能情况构成的集合通常称为 状态空间 ,而程序的运行则是对于状态空间的遍历,算法和数据结构则通过划分、归纳、提取、抽象来帮助提高程序遍历状态空间的效率。
递推和递归就是程序遍历状态空间的两种基本方式。
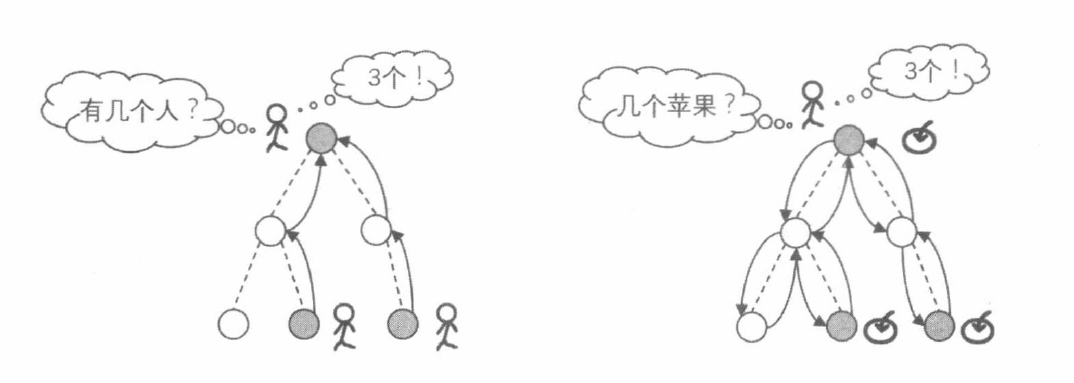
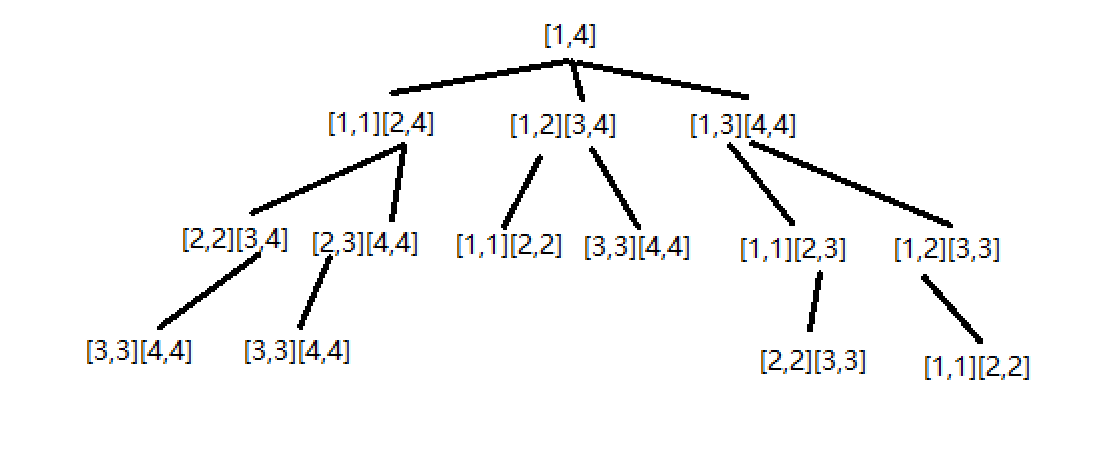
以已知的 问题边界 为起点向 原问题 正向推导的扩展方式就是递推。然而在很多时候,推导的路线难以确定,这时以 原问题 为起点尝试寻找把状态空间缩小到已知的 问题边界 的路线,再通过该路线反向回溯的遍历方式就是递归。我们通过下面两幅图来表示递推与递归的区别。
1.6.1、递归
在分治算法一节中,我们已经提到过递归,我们用 子问题 的角度来不断将问题的规模缩小,如果 原问题 与 子问题 的处理方法相同或类似,那么我们就可以用 递归函数 来实现分治算法。
递归函数 是指自己调用自己的函数,是一种设计算法时的一种编程技巧。 如果确定了用递归法解题,思考的重点应该放到建立原问题和子问题之间的联系。有的问题有很明显的递归结构,但是需要仔细思考,才能正确的转化为结构相同的子问题。
对于递归算法,我们让程序在每个变换步骤中执行三个操作:
- 缩小问题状态空间的规模。这意味着程序尝试寻找在
原问题与问题边界之间的变换路线,并向正在探索的路线上迈出一步。 - 尝试求解规模缩小以后的问题,结果可能是成功的,也可能是失败。
- 如果成功,即找到了规模缩小后的问题的答案,那么将问题扩展到当前问题。如果失败,那么重新回到当前问题,程序可能会继续寻找当前问题的其他变换路线,直至最终确定当前问题无法求解。
后两点尤为重要,其一是 如何尝试求解规模缩小以后的问题。因为规模缩小以后的问题是原问题的一个子问题,所以 我们可以把它视为一个新的原问题 由相同的程序(上述三个操作)进行求解,这就是所谓的 自身调用自身。
其二是 如果求解子问题失败,程序需要重新回到当前问题去寻找其他的变换路线,因此把当前问题缩小为子问题时所做的对当前问题状态产生影响的事情应该全部失效,这就是所谓的 回溯时还原现场。
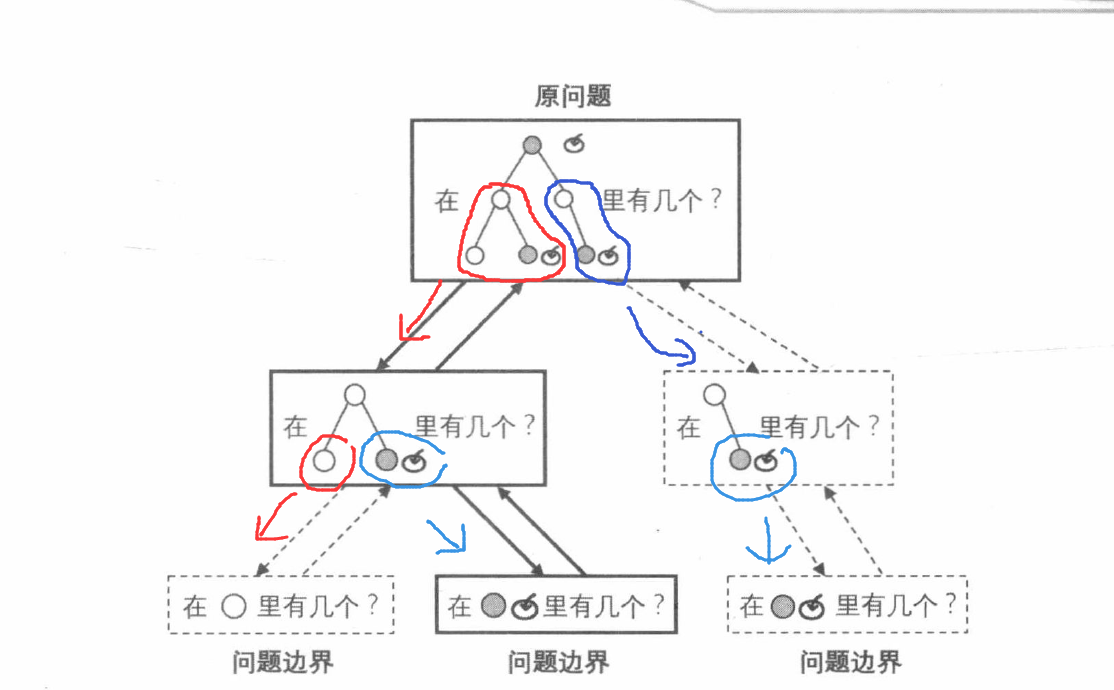
整体的递归思想如图
可以看到,递归程序的基本单元是由 缩小,求解 ,扩展 组成的一种交换步骤,只是在 求解 时因为问题的相似性,不断重复使用,直至在已知的问题边界上直接确定答案。
1.6.2、递推
递推与递归有着很多的相似之处,甚至可以看做是递归的反向。递归的目的性很强,只解需要解的问题,而递推有点 步步为营 的味道,我们不断的利用已有的信息推导出新的东西,而递归是一个构造出了一个通过简化问题来解决问题的途径。
利用现有信息得到新的信息,是递推的精髓。
1.6.3、两者的区别
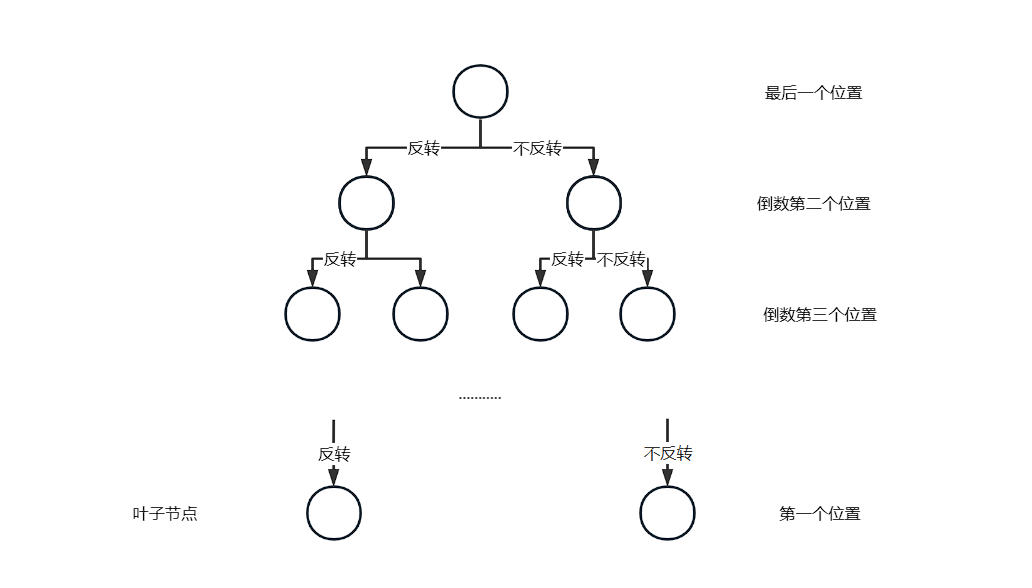
以
CF1271B为例,来源 Acwing
个砖块排成一排,从左到右编号依次为 。
每个砖块要么是黑色的,要么是白色的。
现在你可以进行以下操作若干次(可以是 次):
选择两个相邻的砖块,反转它们的颜色。(黑变白,白变黑)
你的目标是通过不超过 次操作,将所有砖块的颜色变得一致。
输入格式
第一行包含整数 ,表示共有 组测试数据。
每组数据第一行包含一个整数 。
第二行包含一个长度为 的字符串 。其中的每个字符都是
W或B,如果第 个字符是W,则表示第 号砖块是白色的,如果第 个字符是B,则表示第 个砖块是黑色的。输出格式
每组数据,如果无解则输出一行 。
否则,首先输出一行 ,表示需要的操作次数。
如果 ,则还需再输出一行 个整数,。其中 表示第 次操作,选中的砖块为 和 号砖块。
如果方案不唯一,则输出任意合理方案即可。
数据范围
,。
输入样例:
输出样例:
首先我们用递归的思想来看待这个问题,我们将所有的状态空间表示出来,下图的一条路径就表示一种操作的策略,当有 个砖块时,我们要递归出所有的情况的话,需要的时间复杂度是指数级别的 这显然是个非常大的数字,我们将会计算很久很久.....
现在我们从问题本身出发总结出以下几个性质
- 最终的状态只有两种,全黑,或是全白,当然上图的路径也最后只有 条,且有可能在整个状态空间中没有这两条路径(也就是输出
-1的情况) - 第一个或者最后一个砖块的颜色仅与自身是否反转有关,我们以第一个砖块为例。第一个砖块是否反转一旦确立,他将会影响第二个砖块,同时也让他是否反转也确立,如此下去我们就能找到想要全白或全黑的反转方法。
我们相当于从上图的最后一步,逆着这棵递归树而上,找到了最终的方案,这就是前文提到的 递推是递归的反向。
2、数据结构
2.1、C++类
2.1.1、五大成员函数
在定义一个类时,我们会显式或隐式地指定对此对象的拷贝,移动,赋值和销毁时做什么。
一个类通过定义五种特殊的成员函数来控制这些操作:拷贝构造函数(copy constuctor),移动构造函数(move constructor),拷贝赋值运算符(copy-assignment operator),移动赋值运算符(move-assignment operator) 和析构函数(destructor)。
拷贝和移动构造函数定义了当用同类型的另一个对象初始化本对象时做什么。
拷贝的移动赋值运算符定义了将一个对象赋予同类型的另一个对象时做什么。
析构函数定义了当此类型对象销毁时做什么。
2.1.1.1、拷贝构造函数
拷贝初始化是一种使用等号 = 或花括号 {} 来初始化一个对象的方式,它会调用类的拷贝构造函数或移动构造函数。拷贝构造函数的第一个参数必须是一个引用类型。
拷贝初始化与直接初始化以及移动初始化的区别。
一些常见的调用拷贝初始化的情况有:
-
将一个对象作为实参传递给一个非引用类型的形参
-
从一个返回类型为非引用类型的函数返回一个对象
-
用花括号列表初始化一个数组中的元素或一个聚合类中的成员
-
当用类的一个对象去初始化类的另一个对象时
2.1.2、模板
2.1.3、STL
2.1.3.4、string
const CharT* c_str() const noexcept;返回指向拥有数据等价于存储于字符串中的空终止字符数组的指针。
如果不用 strcpy 复制的话,c_str() 是无法修改的!
一般来说c_str() 不会单独出现,都是和其他函数一起使用。
CharT& front();访问首字符
CharT& back();访问末尾字符
size_type size() const noexcept;返回字符个数
size_type length() const noexcept;返回字符个数
void clear() noexcept;清除内容
iterator insert( const_iterator pos, CharT ch );
iterator insert( const_iterator pos, size_type count, CharT ch );
template< class InputIt > iterator insert( const_iterator pos, InputIt first, InputIt last );
2.2、表,栈和队列
表 ADT 有两种流行的实现方法。
vector 提供表 ADT 的一种 可增长的 数组实现。使用 vector 的有点在于它是以常数时间可索引的。缺点是插入新项和删除现有项的代价高昂,除非变化发生在 vector 的尾端。
2.3、二叉树
二叉树是一棵树,其中每个结点都不能有多于两个的儿子。
一棵二叉树由一个根和两颗子树 和 组成, 和 均可能为空。
二叉树的一个性质是平均二叉树的深度要比结点个数 小得多,分析表面,其平均深度为 ,而对于特殊类型的二叉树,即 二叉查找树 ,其平均深度为 。遗憾的是,这个深度是可以大到 的。
后序,中序建树
2.4、二叉搜索树
二叉树的一个重要的应用是它们在搜索中的使用。顾名思义,一棵二叉查找树是以一棵二叉树来组织的。这样一棵数可以用链表数据结构来存储,其中每个结点就是一个对象。
二叉搜索树中的关键字总是以满足 二叉搜索树 的性质来存储:
设 是二叉搜索树中的一个结点。如果 是 左子树中的一个结点,那么 。如果 是 右子树中的一个结点,那么 。
如果我们对一个二叉搜索树进行 中序遍历 那么输出的结果将是个有序序列。
下面是
BinarySearchTree的接口
部分函数的实现版本
2.5、AVL
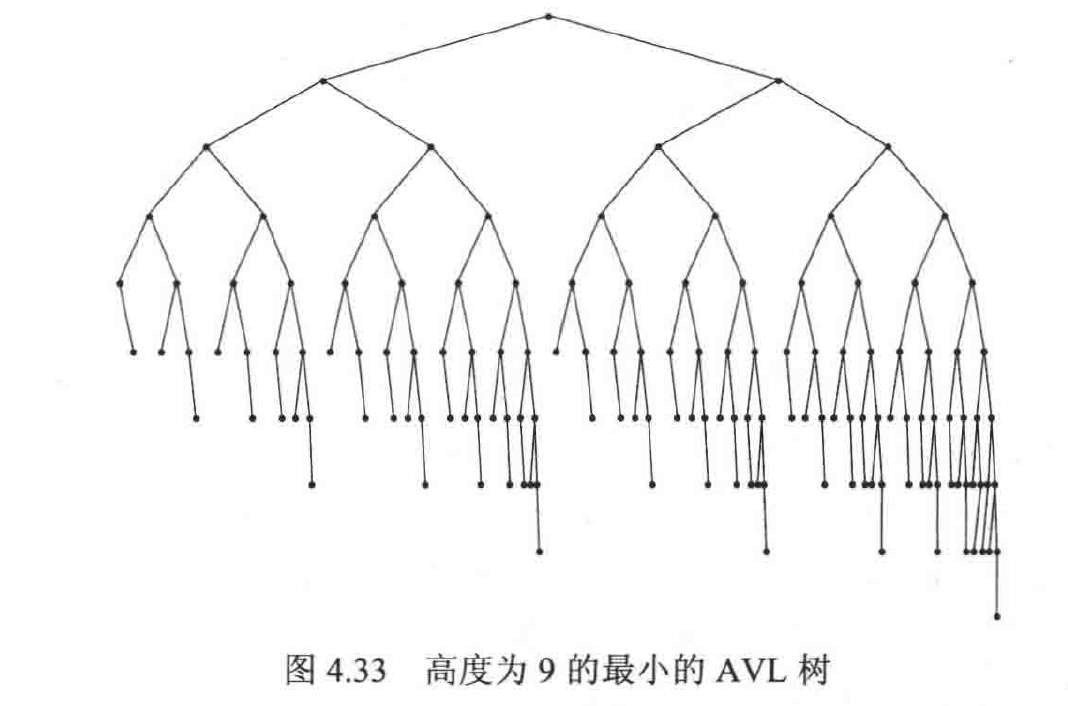
AVL树是带 平衡条件 的二叉搜索树。这个平衡条件必须要容易保持,而且它保证树的深度是 。一棵 AVL树 是其 每个结点的左子树和右子树的高度 最多差 1 的二叉搜索树(空树的高度定义为 )。每个节点会在其结构中保留高度信息。可以证明,一棵 AVL 树的高度最多为 。
除去可能的插入和删除外,所有的树的操作都可以以时间 执行。当进行插入操作时,我们需要更新通向根节点路径上那些节点的所有平衡信息。
核心代码
2.6、Treap
2.7、Splay
2.8、红黑树
2.9、B树
2.10、Fenwick
定义 为一个区间操作(含单位元和逆元的关联函数), 表示长度为 的一个数组。
树状数组是这样的一个数据结构:
- 在给定区间 中计算 的函数值在 的时间复杂度。
- 在 的时间内更新单点值。
- 仅需要 的空间,换句话说所要求的空间与元素数组相同。
- 易于使用和编写代码,特别是在多维数组的情况下。
树状数组最多的应用便是区间求和。(即 )。
Fenwick 树又叫做 Binary Indexed Tree 树状数组,或者直接叫做 BIT。他第一次出现在论文 A new data structure for cumulative frequency tables(Peter M. Fenwick, 1994) 中。
2.10.1、概述
为了简单起见,给定一个数组 ,我们要实现的是两个操作:(1)求区间 的所有元素之和;(2)支持对原数组中的值进行单点修改。
树状数组用一个数组 来表示 ,在上述问题中它的每一个元素等于 数组中一段区间 的和:
是一个函数满足 ,换句话说, 存储的是从 开始向前到 这个位置的这一段区间的所有元素和,而 的值需要通过 这个函数计算而得,我们会在之后定义这个函数。一个数据结构之所以称为 树,是因为用树的形式能够很好地表达这个数据结构的核心思想,虽然我们并不会严格用树的形式来定义这个数据结构。
注意:树状数组这里用的是从 开始的下标。实际上可能还会使用基于 索引的树状数组。因此,您还可以在实现部分中找到使用基于 的索引的替代实现。这两个版本在时间和内存复杂度方面是相同的。
现在我们用一些伪代码来表示两个操作:求得 的和,更新 这个位置的值。
sum 函数的运行流程如下:
- 首先,将区间 (即 所代表的值) 加到
res中。 - 然后,
跳到区间 ,并将这个区间的值加到res中。 - 继续
2的操作直到跳到区间 ,算法停止返回答案。
increase 函数的运行和 sum 类似,区别在于 跳 不是向下跳,而是向上跳。
很容易能够看出 sum 和 increase 的时间复杂度取决于函数 ,有多种定义它的方式,只要最后满足 ,对于所有的 。如果我们让 那么 ,就回到了一个数一个数加的算法了。我们也可以让 ,这就会把 数组变成一个前缀和数组,虽然我们可以在 的时间复杂度内求和,但是更新操作是非常慢的。树状数组算法最聪明的点在于,他使用了一个全新的 函数使得最后两个操作都达到 的时间复杂度。
可能看完伪代码后,读者可能无法理解这个过程,现在您仅需知道,由于每个 中的元素(即树状数组中所存储的值)代表的是向前一段区间的和,通过
while中定义的迭代方式,我们最后会得到所有的 中的和。也就是说res遍历到的区间最后会组成 。上文提到的。
2.10.1.1、全新的 函数定义
函数的定义为:去掉 的二进制表示中最后一个 所表示的值。
使用位运算可以很容易的计算出最后一个 所代表的值:
是按位与(AND)操作。通过上文,利用 函数,针对不同的 我们对区间 进行了划分。这个划分与二进制是紧密相关的(从 函数的定义可以看出)。对于 这个区间来说,如下图我们将划分为 三个区间。
通过观察 的二进制我们可以发现,三个区间的长度正好就是 的三个 的十进制表示!
这就是名称 Binary Indexed Tree 的由来, 中每一个位置存储的区间长度为 的二进制表示中最小的 以及后续的 组成的十进制值。我们将最后一个 删除之后(即计算 ) 就可以得到下一个区间值。
2.10.2、实现
2.10.2.1、在一维数组中求区间和
2.10.2.2、线性构造
2.10.2.3、查询一维数组中 的最小值
2.10.2.4、二维数组求和
2.10.3、不同操作的树状数组
2.10.3.1、单点更新、区间查询
2.10.3.2、区间更新、单点查询
2.10.3.3、区间更新、区间查询
2.10.4、二维树状数组
2.11、Segment Tree
前言:本节翻译自Segment Tree - Algorithms for Competitive Programming (cp-algorithms.com) ,有些图是自己加的,原文中的部分英文表述,我换成了更合适的中文。
如果理解不了本文中的描述,首先是本人的文字能力不足导致的,其次还可能是读者在前置知识点
递归,分治,树,二叉树的树上搜索,位运算上可能还没有理解到位。本文的主要目的是详细的介绍线段树这一知识点,所以默认读者已有以上的编程经验,如果用过多的文字来描述上述知识点就有点本末倒置了。
线段树是一种存储区间信息的数据结构,同时也是一个二叉搜索树。它能高效的查询一段区间的信息,同时还足够灵活满足修改区间信息等操作。比如查询数组中一段连续区间的和,或者在 的时间内查询区间的最小值。除此之外线段树还允许修改数组中单个位置的信息,甚至能够同时修改整个数组。
线段树可以很容易地推广到更大的维度。比如,在二维线段树中可以在 的时间复杂度内求子矩阵的最小值或者其和。
重要的是线段树只需要线性的内存空间,长度为 的数组,只需花费 的空间来建立线段树。
我们从建立一个最简单的线段树开始。我们想高效的求得一个数组区间内的元素和。问题的标准定义如下:
给定一个数组 ,线段树要能够求的数组区间 的总和(即计算 ),同时能够修改任意一个元素的值(即修改 )。线段树需要在 的时间内完成这两个操作。
这是对简单方法的改进。对于一个普通数组来说可以在 的时间内修改一个元素的值,但是求和需要 的时间。如果我们使用前缀和算法那么求和可以在 的时间内完成,但是修改一个元素的值需要 的时间。
2.11.1、线段树的结构
当我们在解决数组段的时候可以采用分治的思想。
我们计算并存储整个数组中元素的和,即 。 我们可以将数组划分为 ,以及 其中 ,计算并存储它们的和。这两个区间又用相同的折半方式继续划分,直到区间的大小为 。
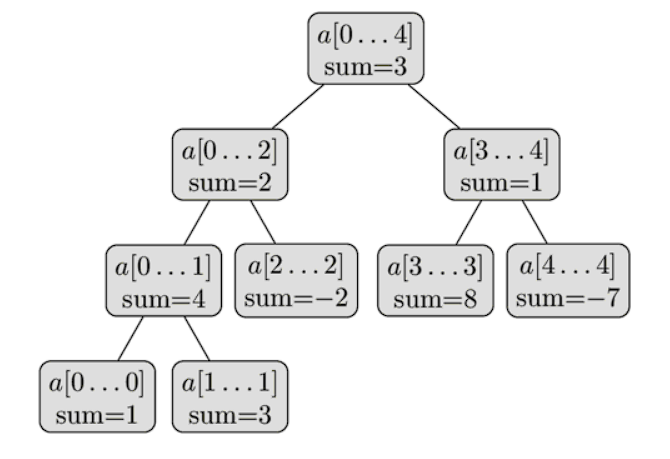
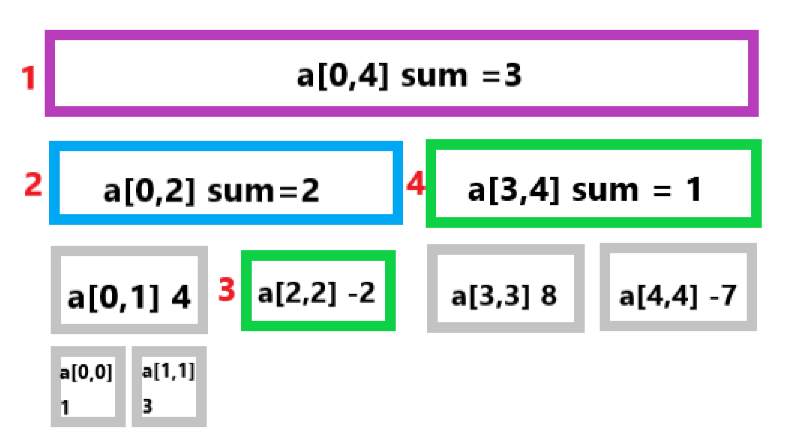
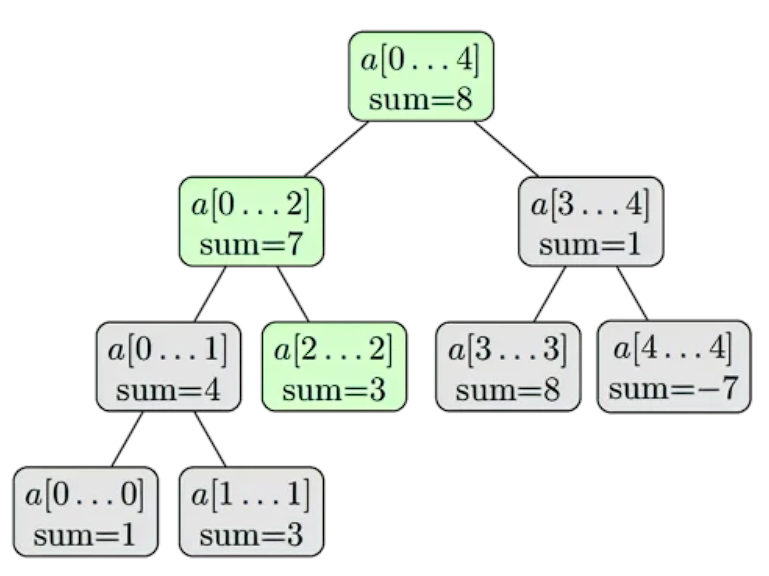
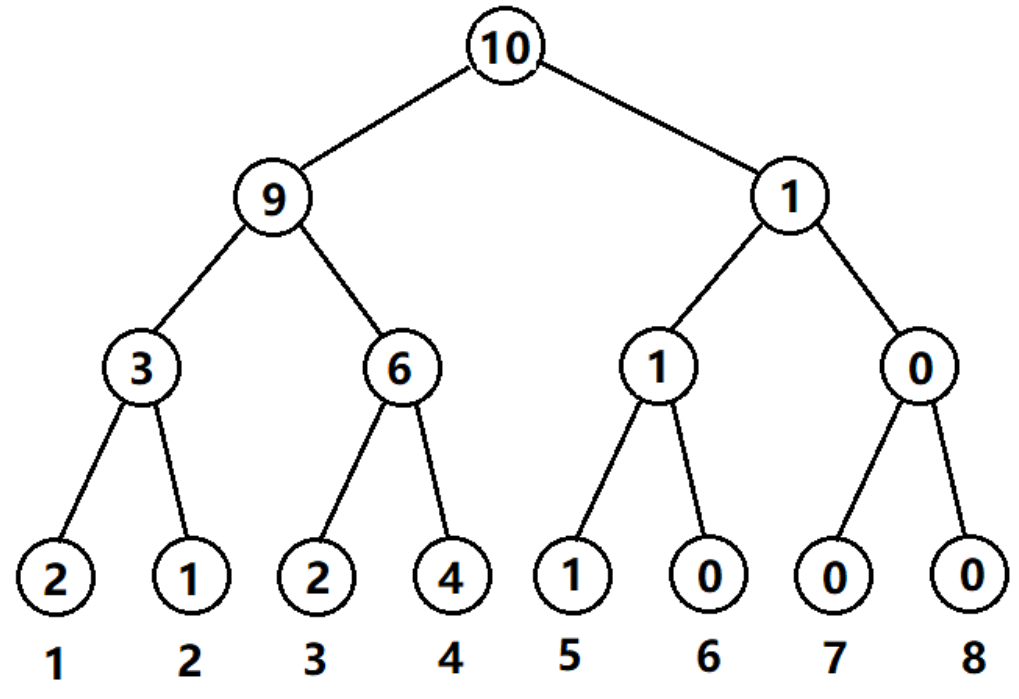
我们可以把这些线段看成是一个完全二叉树:根节点代表区间 ,除了叶子,每个结点都有两个儿子,代表进一步划分的区间。这就是为什么这种数据结构叫做线段树(树的每个结点都代表一个段),尽管在大多数的实现代码中并没有显示的定义树的结构。下面是一个线段树的可视化表达,表示一个数组 a={ 1,3,-2,8,-7 }。
从这个线段树的简单描述中,我们可以看出线段树只需由线性个结点组成。该树的第一层有一个根节点,第二层有两个结点,第三层有4个结点,直到结点数量达到 。因此在最坏的情况下线段树的节点可以用下面的总和来估计:
值得注意的是,当 不是 的幂次方时,线段树的最后一层将不会被填满。从上图中就可以看到这种情况。对于每一个被填满的层次,都包含了完整的 [0,n-1] 区间,层与层的区别在于划分不同,越深的层次划分的越细致,每个区间代表的长度越小。
基于以上事实,我们可以看出线段树的高度为 ,因为从根到叶的过程中线段所代表的区间长度大约减少了一半。
2.11.2、建树
在建树之前,我们需要先决定:
- 每个结点存储什么值。比如,在求和线段树中,一个结点存储的值为区间 中所有元素的和。
- 将线段树中的两个兄弟节点合并的操作如何进行。比如说,在求和线段树中,对于 与 合并为 时(我们假设 ),我们需要把两个结点的和加起来。
需要注意的是,在线段树中所有叶子结点都代表着原始数组(即 )中的一个元素(也可以看做长度为 的区间)。在这些值的基础上,我们可以计算前一层的值,通过上面我们定义的合并操作。然后不断向上重复,我们就可以得到根节点的值。这是上文提到的折半划分的逆运算,被划分的两个区间信息确定后,向上合并为被划分的区间的值。
从递归的角度可以更好的描述这个过程,即从根节点递归到叶节点。在非叶子节点中,建树的过程如下:
- 递归的构造他的两个子节点。
- 合并两个子节点的值,从而构建自身这个节点。
如果递归到了叶子节点(递归的边界),即上文提到的区间长度为 的节点,那么我们直接把原始数组的值赋值过去就可以了(这是针对于求和线段树,对于不同的问题构造方式可能会不同)。
我们从根节点开始执行这个构造过程,所以到最后我们可以遍历到整棵树。
整个构建的时间复杂度为 ,假设合并操作的时间为常数(合并操作被调用 次,这等于线段树的内部节点数)。
2.11.3、求和
现在我们需要解决区间和询问问题。对于输入的两个数字 , 我们需要在 的时间复杂度内计算出区间 的和。
为解决这个问题,我们需要进行树上遍历用提前计算好的区间和(在建树时存储的值)来组成我们的答案。假设我们现在遍历到了表示区间 的节点上。现有以下三种情况。
-
最简单的情况便是当前所在的区间为 的子区间,那我们直接返回答案就好了。( 且 的情况也属于这种情况)。
-
还有可能我们要查询的区间 完全属于当前节点的左儿子所代表的区间(),或者右儿子所代表的区间( ,其中 )。在这种情况下,我们可以直接转到相应的子节点中,并对子节点继续从这三种情况中进行处理(该过程是递归进行的)。
-
最后一种情况,查询的区间与左右儿子所代表的区间均相交。在这种情况下,我们没有其他选择,只能进行两次递归调用,每个子节点调用一次。首先我们到左子结点,计算这个节点的部分答案,然后去到右边的子节点,计算这个节点的部分答案,然后把两个答案相加。
可以看出递归的边界是 1 所对应的情况,2,3 两种情况最终都会成为情况1 在递归树中的父节点。
因此,求和查询用一个函数来处理,该函数使用左子节点或右子节点递归调用自己一次(对应上文的 2 两种情况);或者使用左子节点和右子节点递归调用自己两次(对应上文的3,将查询拆分为两个子查询)。当前所在区间成为查询区间的子区间时,直接返回在建树时预先计算好的区间和(即当前节点存储的值)。
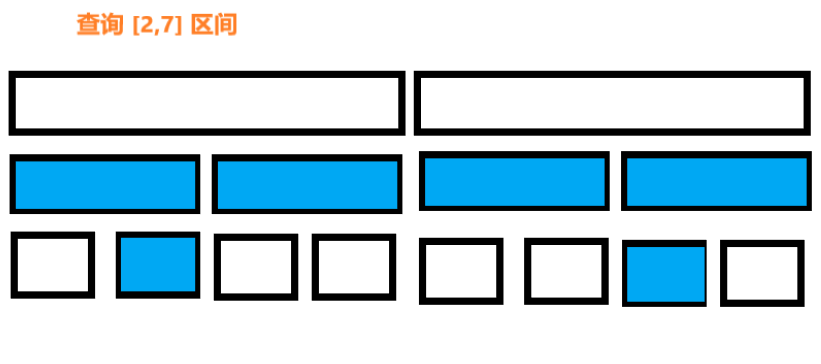
查询区间和的过程,是一个树上遍历的过程,遍历树中所有重要的节点,使用预先计算好的区间和。这个过程的图像描述如下图。还是上文的数组 a={ 1,3,-2,8,-7 },我们现在想要计算 这个区间的和。紫色对应情况3 的区间,蓝色对应情况2的区间,绿色对应情况1 的区间。灰色表示没有遍历到的区间。区间左侧文字为递归的顺序。
最终我们得到的结果是 。
现在可以回答为什么这个算法的时间复杂度是 。为了展示这个复杂度,我们来看看树的每一层。可以证明,对于每一层,我们只访问不超过四个顶点。同时树的高度为 ,总的访问个数最多为 ,忽略系数就是 。
我们可以通过归纳法证明这个命题(每层最多有四个顶点)是正确的。在第一层,我们只访问一个顶点,根顶点,所以这里我们访问的顶点少于四个。现在我们来看一个任意的一层。根据归纳假设,我们最多访问四个顶点。如果我们最多只访问两个顶点,那么下一层最多有四个顶点。这是微不足道的,因为每个顶点最多只能引起两次递归调用。假设我们访问了当前层中的三到四个顶点。从这些顶点出发,我们将更仔细地分析中间的顶点。
由于查询的是连续子数组的和,这些所有的子区间组成了一条区间链,中间的部分都属于情况 1 被 [l,r] 完全覆盖,因此这些顶点不会进行任何递归调用。所以只有最左边和最右边的顶点才有可能进行递归调用(图中第二层)。这些最多只会创建四个递归调用,所以下一层也会满足这个结论。我们可以说,一个分支接近查询的左边界,第二个分支接近查询的右边界。
2.11.4、单点更新
现在我们需要完成第二个任务,修改单个结点的值,即修改原始数组中 (修改值或是增加值原理是一样的)。我们将会重建部分线段树,使得他符合我们修改后的数组。
单点更新操作比求和操作更加简单。由于线段树的每一层都是对整个原始数组的不同划分,因此如果修改了一个点的值,每一层有且仅有一个节点将被修改,那么时间复杂度将会是 。
很容易看出,更新请求可以使用递归函数来实现。遍历到任意一个结点时,继续向下递归包含 的子区间(只存在于左子区间,或者是右子区间),在回溯的时候会重新计算其和值,类似于在构建方法中完成的方式。
我们继续使用上面的数组 a={ 1,3,-2,8,-7 }。执行修改操作使得 。三个绿色的节点将会被访问同时修改其表示的区间和的值。
2.11.5、实现
主要考虑的是如何存储线段树。当然我们可以用一个结构体来表示一个对象,这些对象存储区间的端点、区间和以及指向其子顶点的指针。然而,这需要以指针的形式存储大量冗余信息。我们将使用一个简单的技巧,通过使用隐式数据结构来提高效率:仅将总和以及所代表的区间端点存储在结构体数组中(类似用于二进制堆的方法)。
线段树节点的存储有很多的形式,这与不同人的喜好有关,本文仅介绍我自己喜欢使用的方式,即用结构体存储节点所表示的端点以及区间和。这样做的好处在于,写递归函数的时候少传递 个参数来表示当前访问到了那个节点,而直接从节点中取得。
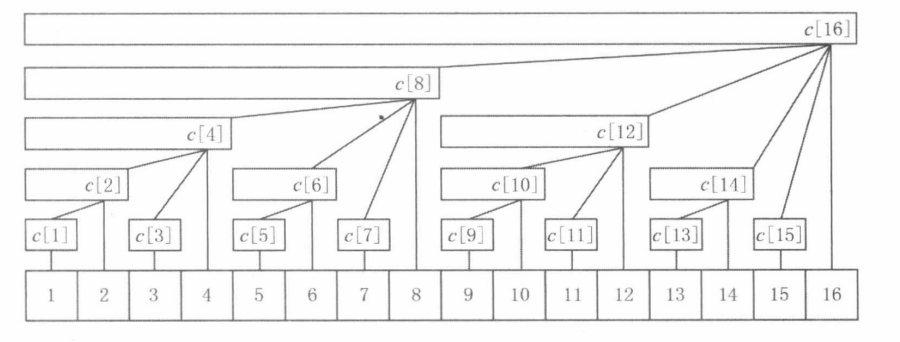
下标为 的结构体数组存储根节点的信息,他的两个子区间的信息分别存储在下标为 , 的位置。我们可以用 i<<1 的方式快速找到 节点的左儿子,用 i<<1|1 的方式快速找到 节点的右儿子,一个结点的父节点可以用 i>>1 的方式获取。这是非常重要的性质!
如之前提到的,线段树的总节点数要开到 ,可能会有多余的空间出现,但是为了不出现段错误,我们统一都初始化为 。
对于 的解释:
- 如果 为 的幂次方,那么就不会出现有空节点的情况,存储线段树的二叉树变为满二叉树。在此情况下,线段树的节点个数为 ,有 个叶子节点,以及 个内部节点。
- 如果 不是 的幂次方,那么需要开 层,需要多乘一个 ,所以将会开到 。
定义代码:
另外,为了方便代码编写以下是我将会定义的宏:
ls表示左子区间的编号,rs表示右子区间的编号,L表示当前区间的左端点,R表示当前区间的右端点,mid表示当前区间的中间位置。
从给定 数组中构造线段树的过程如下:它是一个递归函数,参数为 rt 表示当前遍历的节点的下标,l,r 表示当前处理的节点对应的区间。在主程序中将会以 rt = 1,l = 1, r = n 被调用。if 内的代码对应的是叶子节点的处理方式,if 下面的代码对应的是非叶子节点的处理方式。
build 函数中第一行 sum 值先赋值 作为临时的值,叶子结点的 sum 值由第十行赋予,非叶子节点的 sum 值由 push_up 函数赋予。需要注意的是,13,14 行的代码 ls,rs,mid 均为我定义的宏(详见上文),如果没有定义宏的话,代码将会报错。定义宏之后,代码将会更加的简洁,方便检查错误(血泪教训)。读者可以试试对比定义宏的代码,和不定义宏的代码在阅读上的体验。
求和函数也是一个递归函数,它的参数有当前处理的结点编号 rt ,所求和的区间 l,r (有些线段树的写法还有有 tl,tr 两个参数用来表示当前处理节点所对应的区间端点,但是本文的线段树结构中已经存了这两个信息,所以就不用在函数中定义这两个参数)。函数中三个 if 对应着上文提到的不同情况。第一个 if 为递归的边界,后面两个 if 将递归向下进行,搜索长度更小的区间。需要注意的是函数中 L,R,mid,ls,rs 均为宏,如果没有上文的宏定义,代码将会报错。
最后是单点更新,这个函数有三个参数表示当前节点标号的 rt ,表示修改a[i] = x 中的 i 也就是待修改的下标 pos(这个下标是针对原始数组的),以及 val 表示 x ,即修改之后的值。
这里的代码结构类似于快速选择算法的 quickselection 函数。
2.11.6、小结
线段树是一颗二叉搜索树,在定义时,我们采用结构体数组的方式,而非指针节点。需要强调的是,线段树代码实现有很多版本,每个人选择自己喜欢的方式就可以了,我最开始学习线段树的时候,网上每一篇题解都用不同的风格来写,很是头痛,但是只要原理懂了,实现只是方式上的不同而已。我在上文定义的 5 个宏 L,R,mid,ls,rs 是我的编程经验,读者完全可以不用宏。
建树过程的本质是在树上进行 深度优先搜索,如果读者没有类似的编程经验,可能阅读本文会有些吃力,建议先去学习这个模块的知识。搜索到叶子节点时将会把原始数组的值赋给区间节点,回溯时会把子区间信息合并到本区间。当最后回溯到根节点(即编号为 1 的节点时)整棵树就建立完成了,每个节点都保存了它所代表的区间和以及区间的左右两个端点。
更新操作是简化的建树过程,建树时会进入两个子区间,而单点更新时只会进入其中一个,最终形成一条根节点到叶节点的路径。向下递归的过程是查找节点的过程,而向上回溯的过程是更新区间和的过程。
区间和查询操作的核心是理解三种情况,对于每个遍历到的节点我们都需要判断它属于三种情况的哪一种情况,并做出相应的处理。
push_up 函数是不必要的函数,完全可以用一行代码来代替,这也是一种编程经验,写成内联函数的形式不会影响算法的时间复杂度,还可提升代码的可读性。把相似的代码抽象成一个函数,是一个良好的编程习惯。
2.11.7、线段树的应用
线段树是一种非常灵活的数据结构,允许在许多不同的方向上进行变化和扩展。让我们试着把它们分类如下。
2.11.7.1、最大值
让我们稍微改变一下上面描述的问题的条件:现在我们将进行最大值查询,而不是查询总和。该树将具有与上述树完全相同的结构。仅把和的存储变为最大值存储,我还需要修改区间合并的方式,区间和查询将变为区间最大值查询同样要对三种情况进行处理,单点更新函数与建树函数仅需将 sum 改为 ma 就可以了。
当然,这个问题可以很容易地变成计算最小值而不是最大值。
2.11.7.2、求最大值的同时保存其出现的次数
这个任务与前一个任务非常相似。除了求最大值,我们还要求最大值出现的次数。为了解决这个问题,除了最大值之外,我们还存储了它在相应段中的出现次数。
单点更新函数与上节没有任何变化,push_up 函数为了维护新的信息做了较大修改,代码写的比较简洁可能需要多思考下。build 函数只需要在 if 中多初始化 cnt=1 就可以了。
改动最大的是查询最大值函数,并为了代码简洁我们新加了一个combine 函数来维护查询的答案(如果不这样做的话,在后面两个 if 中会有很多重复代码,形成冗余)。
2.11.7.3、求 最大公约数/最小公倍数
在这个问题中,我们要计算给定数组范围内所有数的最大公约数(greatest common divisor(gcd))或是最小公倍数(lowest common multiple(lcm))。
可以用完全相同的方式来解决这个问题:在树的每个顶点中存储相应顶点的GCD / LCM就足够了。合并两个顶点可以通过计算两个顶点的GCD / LCM来完成。
这里只给出两个区间合并的代码(这是最终要的),其他部分去上一个问题类似。
2.11.7.4、记录 出现的次数,并求第 的位置
在这个问题中我们需要计算在给定区间中 数字0出现个次数,以及整个数组中第 个 出现的位置(区间内第 个 的求法将在后文出现)。
一样的,我们需要先思考线段树要存储那些值:这次我们只需存储每个区间中存储了多少个 。其他的建树、更新和计算区间出现的 的次数类似于区间求和。
我们主要来解决如何求第 个 的位置。为了解决这个问题,我们要从根节点向下遍历,每次只向左或向右移动到子区间,这主要取决于第 个 在那个区间。计算到底进入那个子区间,我们只需要用到左子区间中的信息。如果左子区间中 的个数大于或等于 ,那么就进入左子区间,否则进入右子区间。需要注意的是如果我们决定要进入右子区间后, 的值需要减去左子区间含有 的个数。
2.11.7.5、找到最小的大于 的前缀和
给定数值 我要尽可能快的找到最小的下标 满足 的和大于或等于 ( 中的均为非负整数)。这个问题和前一个问题的解决办法基本一致。
* 2.11.7.6、找到区间中位置最小的大于 的数
给定 以及区间 找到区间中最小的下标 使得 。对于这个问题线段树中只用存储端点信息以及区间最大值。
我们将这个问题分成两个部分:
- 将当前处理的这个区间转移到 的子区间中,转移时先向左移动(满足最小),如果左子区间无法满足条件或者不在 中再进入右区间。
- 当前区间已是 的子区间后,搜索第一个大于 的位置。
之前我们的搜索过程只有 个搜索函数,在这个例子中由于要考虑两个因素(在 中,最小的 使得 ),所以先满足一个条件,然后再切换搜索目标去满足另一个条件。
2.11.7.7、找到一个区间的最大子区间和
在数组 中给定 ,找到一个连续子区间 ( 且 ) 使其和最大化。和之前一样我们还要能够进行单点修改,原始数组中的数可能为负数,最优的子区间可以为空(其和为 ,这个可以特判一下,不可为空的最优子区间小于 则直接输出 就好了)。
这是线段树非常重要的一个应用。这次我们除了存储端点信息还要存储另外 个值分别是:整个区间和sum,包含左端点的子区间的最大和l_ma(最大前缀和),包含右端点的子区间的最大和r_ma(最大后缀和),整个区间的最大子段和ma。
如何用这些数据构建树?我们再次以递归的方式计算它:我们首先计算左子节点和右子节点的所有四个值,然后将它们组合起来以存档当前顶点的四个值。注意,当前顶点的最大子段和ma可能有三种情况:
- 左子区间的最大子段和
T[rt].ma=T[ls].ma。 - 右子区间的最大子段和
T[rt].ma=T[rs].ma。 - 左子区间的包含右端点的最大和与右子区间的包含左端点的最大和这两者的和
T[rt].ma = T[ls].r_ma + T[rs].l_ma。
因此,当前顶点的最大子段和就是这三个值的最大值。计算最大前缀/后缀和就更容易了,我们只描述最大前缀和的计算方式,后缀的计算方法与其完全类似。答案可能的情况一共有两种:
- 左子区间的最大前缀和
- 左子区间的和加上右子区间的最大前缀和。
同样,取两者的最大值就可以得到最终答案,下面是线段树定义以及合并的代码。
建树与单点修改的代码与之前的模式基本一致,这里就不过多赘述了。现在就只剩下了查询操作,与 求最大值的同时保存其出现的次数 这一节中使用到的方式类似。为了回答这个问题,我们像以前一样沿着树向下走,将查询区间 分解为线段树中的几个子段,并将其中的答案组合为查询的单个答案。我们还需要用到 combine 函数将查询的答案合并就像 push_up 函数一样。
测试题目SPOJ GSS1。
2.11.8、在节点中保存所有子数组
这是一个独立的子部分,与其他子部分分开,因为在线段树的每个节点,我们不以压缩形式存储有关相应区间的信息(最值,区间和,···),而是存储区间的所有元素。因此,根节点将存储数组的所有元素,左子顶点将存储数组的前半部分,右顶点存储数组的后半部分,依此类推。
在该算法最简单的应用中,我们按排序顺序存储元素。在更复杂的版本中,元素不是存储在列表中,而是存储在更高级的数据结构中(set、map等)。但所有这些方法都有一个共同点,即每个顶点都需要线性内存(即与相应段的长度成正比)。
在考虑实现这种线段树时,第一个问题自然是关于内存消耗的。直觉告诉我们这种方式的存储可能是 的,但实际上只需要 的内存。证明思路很简单,线段树的每个满节点的层次,都将把 全部存一次,同时树的高度是 那么总共会存 个元素。
因此,尽管这种线段树看起来很奢侈,但它只比通常的线段树多消耗一点内存。下面描述了这种数据结构的几个典型应用。值得注意的是这些线段树与 2D 数据结构的相似性(实际上这是一个 2D 数据结构,但功能相当有限)。
2.11.8.1、区间内求大于或等于一个特定数的最小数值(不带修改)
给定三个数 我们要找到最小位置 ,使得 。
在线段树的每个顶点中,我们存储相应区间中出现的所有数字的有序排列。如何尽可能有效地构建这样的线段树呢?像往常一样,我们递归地处理这个问题:让左和右子节点的有序列表构造好,再构建当前区间的有序列表。从这个角度来看,操作现在很简单,可以在线性时间内完成:我们只需要将两个排序列表组合成一个,这可以通过使用两个指针对它们进行迭代来完成(类似归并排序的方式)。c++ STL已经实现了这个算法。
merge:归并二个已排序范围[first1, last1)和[first2, last2)到始于d_first的一个已排序范围中。
由于这种线段树的结构与归并排序算法有相似之处,所以这种数据结构也常被称为归并排序树(Merge Sort Tree)。
我们已经知道用线段树节点来存储这种数据会花费 的内存。由于归并的实现方式,他的时间复杂度也是 ,毕竟每个有序序列都是在线性时间内构建。
现在我们来思考如何解决询问问题,就像传统线段树一样,我们从树根沿着这棵树向下走,将 划分为多个分段。很明显,最终的答案是每个分段的答案中数值最小的那个。
假设现在遍历到了线段树的某个顶点,我们想要计算查询的答案,即找到大于或等于给定数的最小值。由于顶点存储了区间的有序排序,我们可以简单地对该列表执行二分查找并返回第一个大于或等于的数字。
因此在树的一个段中的查询时间为 ,整个查询的时间复杂度为 。
0x3f3f3f3f 代表的是一个很大的数,用来表示当前区间中没有答案。
2.11.8.2、区间内求大于或等于一个特定数的最小数值(带修改)
问题描述与上小节相同,上节的解决办法有个缺陷就是如果要进行修改操作的话时间复杂度会非常高。现在我们就需要来解决这个问题,实现 单点修改操作。
解决方案类似于前一个问题的解决方案,但不是在段树的每个顶点用 vector 来存储信息,而是用一个自排序的数据结构,允许快速进行搜索数字,删除数字和插入新数字等操作。由于数组可以包含重复的数字,因此最优选择是数据结构 multiset。
构造这样的线段树的方法与前面的问题基本相同,只是现在我们需要合并 multiset 以及未排序序列。这将使建树过程的时间复杂度达到 (通常合并两个红黑树可以在线性时间内完成,但是 c++ STL 不能保证这种时间复杂度)。
查询函数也几乎是一样的,只是现在应该调用 multiset 的lower_bound 函数。
最后是修改操作,为了实现做过操作,我们将从树顶向下搜索,修改每一个含有这个元素的 multiset。删除原来的元素,插入新的元素。
2.11.8.3、区间内求大于或等于一个特定数的最小数值(分散层叠优化)
和前文的问题一样,我们要找到区间内大于或等于 的最小值,但是这次要在 的时间复杂度内完成。我们将用分散层叠算法(fractional cascading)来优化时间复杂度。
分散层叠是一种简单的技术,可让缩短同时执行的多个二分查找的运行时间。我们之前的搜索方式是将任务分为多个子任务然后独立的进行各自的搜索。分散层叠技术将用单个二分搜索替代其他所有的搜索。
分散层叠最简单、直观的应用便是解决下面这个问题:给定 组已排序序列,我们要找到每一组中大于或等于给定数的第一个数。
我们将合并 个有序序列为一个大有序序列。此外我们将把每个元素 在所有序列中二分搜索的结果存储在一个序列中。因此,如果我们想找到大于或等于 的最小值,只需要执行一次二分查询,便可从索引列表中确定每个元素中的最小值。
2.11.9、区间更新(懒惰传播)
上面讨论的所有线段树问题都是单点更新,然而线段树允许在 的时间内修改整段连续的区间数值。
2.11.9.1、区间加值,单点查询
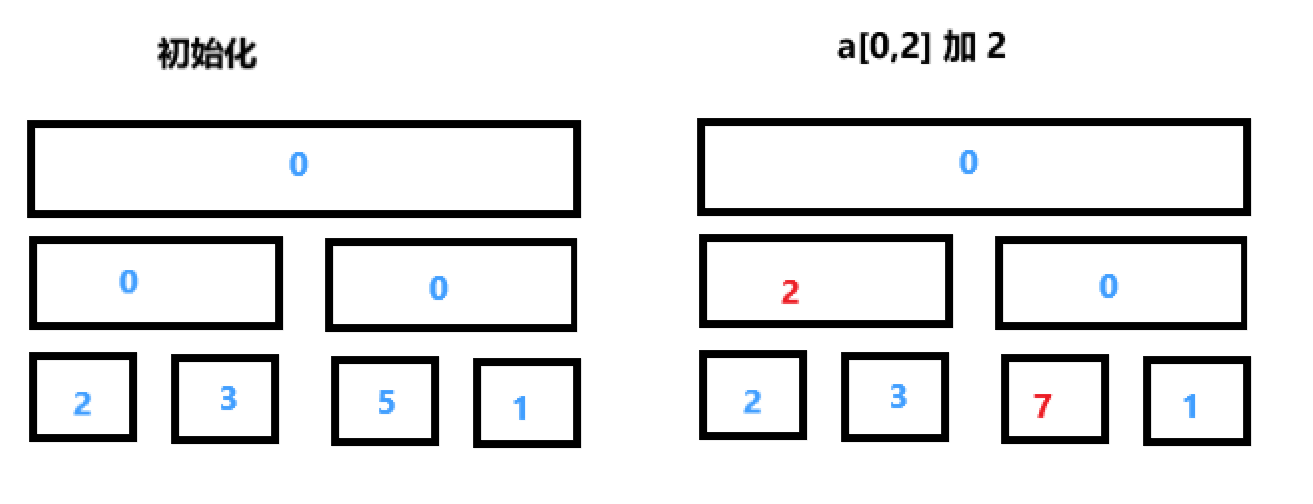
我们从一个简单的例子开始讨论:修改操作将会把 区间中所有的数字加 。第二个查询仅返回一个单点 的值。为了高效处理修改操作,每个结点存储的是这个区间每个数增加的数。比如,执行操作 中所有的数都加 ,那么我们把根节点存储的值加 就可以了。建树的过程可以看做把叶节点都加 。通常来说我们将会把这个添加操作执行 次,但由于我们使用线段树存储区间,所以这种更新方式只用执行 次。
我们用一个例子来说明对于数组 ,初始化之后整个线段树如下图左边所示。现在我们执行更新操作,对 的所有元素都加 ,执行完之后如右图所示。如果我们要查询 的数值的话,那么就会把一直到 对应的叶子节点路径上所有节点的值加起来,即 。
值得注意的是,这次的线段树没有合并操作。
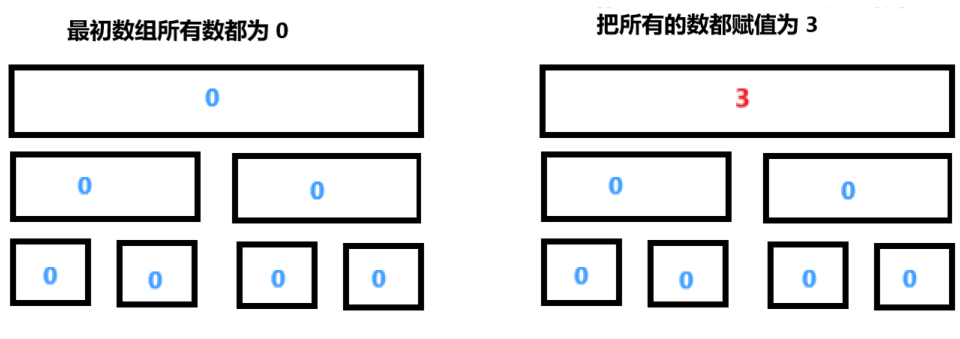
2.11.9.2、区间赋值,单点修改
现在我们要解决的问题是:把 中每一个数都重新赋值为 ,同时还要可以单点查询。
为了执行这个修改操作,我们需要在每个结点存储一个变量用以表示是否相应的区间被一个值覆盖。这就运行我们进行 懒 更新:我们只更新一些节点,让其他节点不着急更新,而不是把所有相关的节点在一次全部更新了。标记顶点意味着,相应区间的每个元素都被赋于相同的一个值。从某种意义上说,我们是懒惰的,延迟了将新值写入所有这些顶点,而只写一部分重要的节点。如果有必要,我们可以稍后再做这项乏味的工作。
例如,如果要把 的所有数字都赋为一个值,那么在线段树中实际只改变了根节点的一个数值。剩下的部分保持不变,尽管实际上这个修改应当改变树中所有节点。
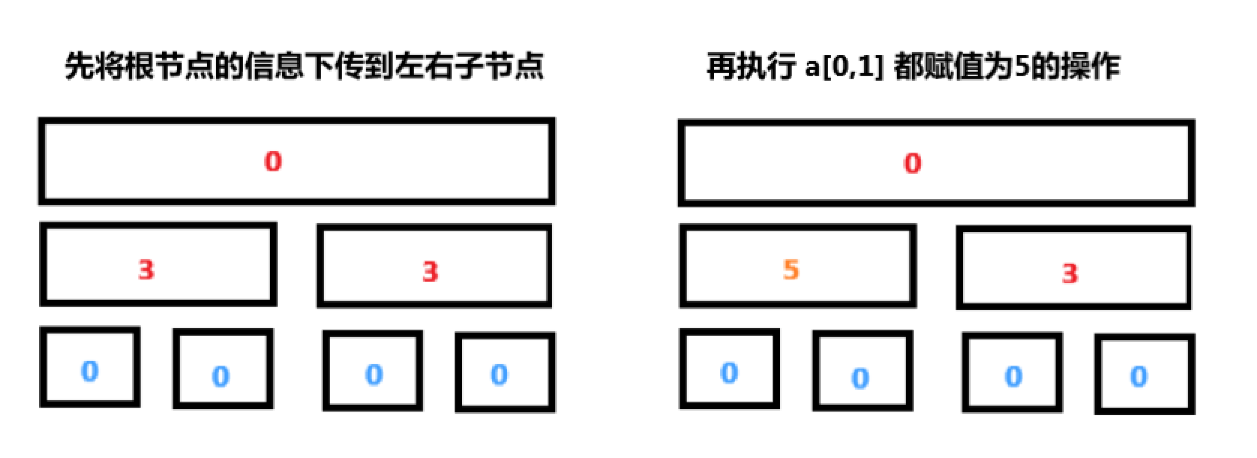
现在来处理第二个操作,将 (数组的一半)的所有数都修改为某个数。为了处理这个查询,我们必须把根节点的整个左子节点中的每个元素赋值这个数字。但在此之前,我们必须先将上次对根节点的赋值进行分发(或者说是向下传递)。这里的微妙之处在于,数组的右半部分仍然是上一次赋予的值,并且现在它没有存储任何信息。
解决这个问题的方法是将根节点的信息推送给它的子节点,也就是说,如果树的根节点被分配了一个数字,那么我们将这个数字分配给左、右子节点,并删除根节点的标记。之后,我们再把新值赋给左子节点,而不会丢失任何必要的信息。
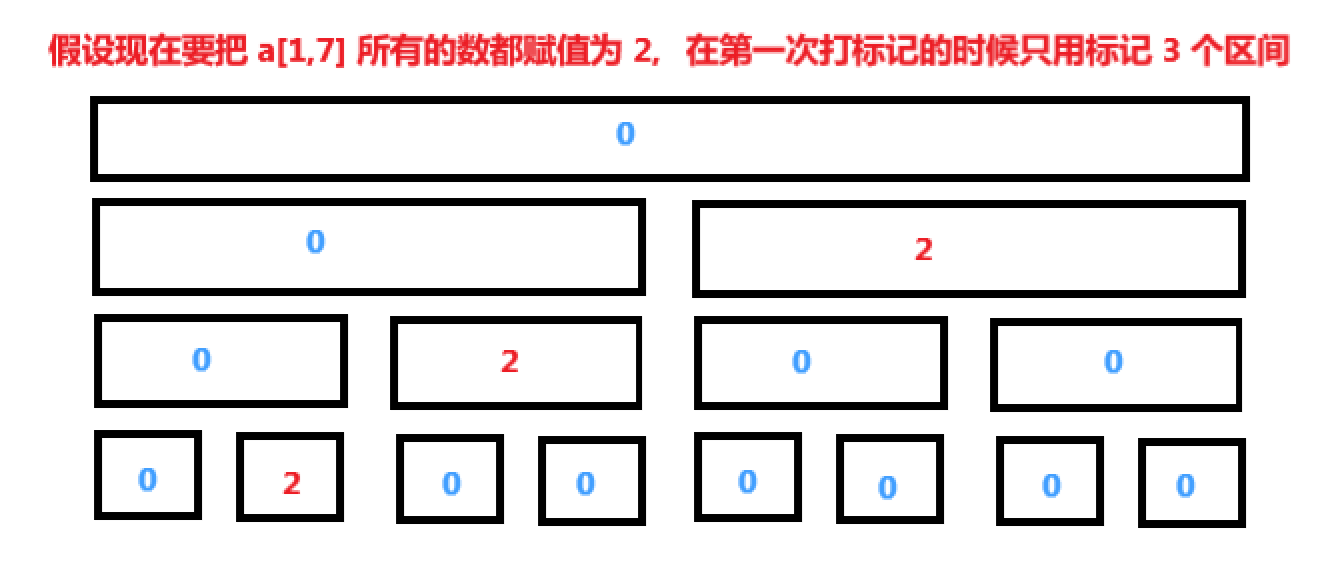
总结一下,我们得到:在树的下降过程中,对于任何操作(修改或查询),我们应该总是先将当前顶点的信息推送到它的两个子顶点。我们可以这样理解这一点,当我们从根节点下降到叶节点时,我们开始修改之前 懒得 修改的节点。在第一次修改时,我们仅仅打了一个待修改的标记,当我们再次要用到这个数据的时候(执行又一次修改或查询),我们才把数据给下传下去。懒(Lazy) 的心态是,现在如果数据还没有用到,那么我们就不着急把他向下传递,如果下面的区间开始要用到这个数据了,那么我们才把数据给他传下去,这是这一节的核心思想。 先把 用最少的区间表示出来,再在这些区间上打上懒标记,这样我们才能做到不会有缺漏,同时效率也是最大化。
除了叶子节点之外,其他位置存储的数据都是待更新的数据,这些值最终会跟随查询操作下传到叶子节点。push_down 函数,用于下传 lazy 标记,和我们之前的 push_up 函数相反。
2.11.9.2、区间加值,区间最值
新的问题是需要在一段区间中加上一个值,同时还要能够查询一段区间的最大值。
所以对于线段树的每个顶点我们必须存储对应子线段的最大值。重要的部分是如何在修改后重新计算这些值。为了解决这个问题,我们需要在单点修改的代码基础上,在线段树定义中多一个 lazy 值(不同于上一节的 marked 标记,这将会存储数值)。lazy 将会存储还未下传给子节点的值,每次向下遍历之前,我们先把当前节点没有下传的信息传递给两个子节点。在 update 与 query 两个函数中我们都会这样做。
2.11.10、扫描线
2.11.11、动态开点线段树
在使用线段树这一数据结构解决问题时,我们可能会遇到以下的情况:区间的范围太大如 ,直接开会爆内存,但是要存的点只有 个。
针对这种情况,动态开点线段树便应运而生了。这种线段树在一开始只会建立一个根节点,其核心思想为:要用到这个节点对应的区间信息的时候才建立相应的节点。它与传统的线段树有以下的不同:
- 树的结构不在是完全二叉树。所以取左右儿子的方式不再是
rt<<1,rt<<1|1,而是在结构体中存储儿子节点的地址。 - 树的空间会在一开始全部开上,但是树的结构不会在一开始就建立好,仅仅在根节点创建好。
build函数与之前的作用不同了,现在的build函数可以直接理解为new Node(),相当于给你一个新的节点的地址。- 在之前的每个节点中,我们会存储节点所代表的区间 (当然也有些传统线段树版本不会存),现在我们不会存了,所以在执行更新,查询等操作的时候在函数头上要多 个参数来表示当前区间的范围。
使用 new 方式获取新的内存,这种方式在算法竞赛中很少使用,我们一般都采用的是使用一个数组和一个指针来模拟内存分配。代码中 T[] 数组的定义方式和之前一样(因为总共需要建立的节点数是没有变的),但是树的建立方式却不同了(后面解释)。 tot 指针就相当于一个指向空闲空间的指针,它和 T[] 数组是动态开点线段树的核心。
在进行查询,更新操作的时候,可能会搜索到没有创建的节点,此时我们直接创建新的节点就可以了。
下面是一个区间加值,区间查询的题目代码与以往不同的是 的值为 ,但最多进行 次操作。
总结:
动态开点线段树是一种新的初始化、存储线段树的方式,其他方面与传统的线段树无异。动态开点是后续知识主席树的前置知识,但它并不是一个很难的知识点。
2.11.12、权值线段树
权值线段树本质上仍然是传统的线段树,唯一的特点在于,它的作用类似于桶。举个例子如果我们要存一个数组 ,那么对应的权值线段长这样:
可以发现每个节点存的值为:区间下标对应的数值在整个数组中出现的次数。这个一特点使得这种线段树有非常广泛的应用,所以我们单独对这种结构的线段树进行研究,并命名为权值线段树。
再重复一次,权值线段树就是一棵普通的线段树,它的特点在于节点存储的值为区间下标对应的数值在整个数组中出现的次数。
细心的同学可能已经发现有问题了,上面一段话中有个词语特别别扭 整个数组?是的,这是权值线段树需要注意的一个事项,权值线段树中的值存的不是某个区间出现的次数,而是整个数组中数字出现的次数。也就意味着权值线段树能进行的查询操作,仅能针对整个数组进行。
这就要引出了我们权值线段树最重要的一个应用:
给定一个数组 ,查询整个数组第 大(小)的元素的数值。P1138 第 k 小整数
我们先用用 动态开点 + 权值 的方式来写这个题。至于为什么要用这个方式来写这个题,我们先按下不表,在后面会解释。
2.11.13、势能线段树
在将势能线段之前,我们先引入势能这个概念。在物理学中势能是一个状态量,比如说重力势能,在重力势能引入后,不管一个物体按多么复杂的路线移动,最后重力势能的变化就只于高度的变化有关。这样的好处是忽略了复杂过程对计算的影响。
同样我们在这里引入势能也是一样的作用。我们来看下面这个例子
1、两个数求 的时间复杂度是 。
2、三个数求 的时间复杂度也是 。
3、 个数求 的时间复杂度是多少呢?
直觉告诉我们,答案是 ,但最终的答案是 。原因在于我们每次两数求 之后的 ,是单调下降的,很快就会下降到 (可能不会,但只会辗转相除 次),那么之后的数再与 求 的时候就直接返回了。
我们将势能的概念引入到 求计算时间复杂度的例子中,这里的势能就是最后 的值,这个值(势能)只会单调的下降,他只会减少 次(基于最初的势能)。
2.11.14、线段树合并
2.11.15、可持续化线段树
2.11.x、习题
Codeforces - Xenia and Bit Operations 单点修改,单点查询
Codeforces - Distinct Characters Queries 区间查询,单点更新
Codeforces - Ant colony 区间 gcd ,区间计数
[P3960 NOIP2017 提高组] 列队
- 测试点的纯暴力写法
2.12、散列(Hash表)
2.12.1、字符串前缀Hash法
str =" ABCACB"
h[0] 表示为 " " 的 Hash 值(一般我们都从 1 开始存储字符串,0 空出来)
h[1] 表示为 " A" 的 Hash 值
h[2] 表示为 " AB" 的 Hash 值
h[3] 表示为 " ABC" 的 Hash 值
Hash 数组就是
str的前缀 Hash值
然后我们把每一个字母映射成一个数(一般直接用ASCII),把它看成 p进制数,同时为了冲突最小化一般 p = 131 or 13331 。
假设 A->1, B->2, C->3, D->4。
那么 " ABCD" 的 Hash值为
可以看到这里的 的次方是递减的,这样的好处是我们在计算前缀值的时候更加方便。如果下一位字母是 E ,其映射值假定为 ,那么 " ABCDE" 的前缀值计算公式为
我们展开 可以得到
就和最开始我们求 的公式是一样的,这就是我们要递减 的原因,通过前缀和的方式来求 hash 值。
Hash 值的求解就是一个 p 进制的数,求其 10 进制值的过程。
如果我们要求整个字符串的一个子区间的 Hash 值(例如上面字符串的 "CD")时,通过一个公式我们可以在 的时间复杂度内得到。
我们找到以 结尾的 h[4] ,即上述公式的 ,后两项刚好就是我们要求的值,我们只需用
通用的公式对于 区间:
下面是代码
2.13、不相交集合并(并查集)
Disjoint Set Union or DSU 不相交集合并,通常又因为它的两个主要操作称为 Union-Find 并查集。
这种数据结构主要提供以下的功能。给定几个分散的集合,DSU 可以做到合并任意两个集合,同时可以指出某一元素所在的集合是哪个。在最经典的实现中,还会有第三个功能,为一个元素建立一个新的集合
make__set(v)为元素 v 创造一个新的几何union_sets(a,b)合并两个特殊的集合(这两个集合分别是a元素位于的集合以及b元素位于的集合)find_set(v)返回含有元素 v 所在的集合。如果满足find_set(a) == find_set(b)就表示两个元素在同一个集合之中,反之则不是。
这个数据结构运行你在近乎 的时间复杂度下进行上诉操作。
但是也存在时间复杂度为 的实习方式,他比上述的版本有更强大的功能。
2.13.1、高效的建立方式
我们将会用树这一结构来存储 DSU,每一棵树代表一个集合,这棵树的根节点作为这个树的代表。简言之就是树的根节点代表一个集合。
最开始一个元素作为一个集合,因此每个结点都形成一棵独立的树。集合合并的过程就是把一棵独立的树变成另一棵树的子树。
这种构造方式意味着我们不得不用一个 parent 数组来存储一个结点的祖先。
2.13.2、一个简单的实现方式
首先,这种实现方式是低效的,但是在之后我们会用两种改进的方法,来使得每一次操作都是接近常数级的时间复杂度
如上文所说,所有的集合信息都将存储在 parent 数组中。
为了建立一个集合 make_union(v) ,我们创建一个根节点为 v 的树,也就是说这个节点的祖先结点是他自己。
在合并操作中 union_sets(a,b) ,我们分别找到 a ,b 结点的根结点是什么(也就是找到两个集合的代表)。如果两者的根结点是相同的,说明他们在同一个集合中,显然集合已经合并了,那就不用做任何其他的操作。如果两者的根节点是不同的,我们随便选一个结点把他的根节点的根节点(显然应该是他自己)设置为另一棵树的根节点。
最后一个操作是查询操作 find_set(v) ,我们只需不断向上递归就能找到这个节点的根节点。递归的边界就是祖先节点为自己的节点parent[v]==v。
然而这个实现方式是非常低效的。他简单写法导致了这个树可能会退化成一个长链。在这种情况下 find_set(v) 的实现复杂度将会是 的。
2.13.3、路径压缩优化
这个优化主要是为了提升 find_set(v) 运作的性能。
如果我们调用 find_set(v) 这个函数,其实我们是找到了 v->p (p为根节点)这条路径上所有结点的根结点。我们可以让这个路径变得更短,通过把这个路径上所有的结点的祖先结点都设置为 p。
新的函数实现为
这个新的实现方式做到了:
- 找到这个元素的根节点(即集合的代表元素)
- 在查找的过程中把这条查询路径变短了,也就是压缩了路径。
这个简单的修改就可以使得 find_set(v) 的平均时间复杂度降到了 。下面的这个改进还会让他变得更快。
2.13.4、通过树高 / 大小作为合并决策
这个优化主要是针对 union_sets(a,b) 。在之前的实现中,我们总是让第二棵树成为第一棵树的子树。在这种情况下,可能让一棵树变成长度为 的长链。本次的优化主要就是为了防止这种情况出现。
有多种策略可以使用,最流行的两种是:
- 以树含有的节点个数也就是树的大小来作为判断标准
- 以树的深度来作为判断标准
两种优化的本质是相同的,都是把值更小的接到值更大的哪里去。
以下为以节点个数为指标的实现方式:
以下为以树高为指标的实现方式:
两种优化方式对于时间复杂度的优化基本上是相同的,在实现中任意一种都是可以的
4、算法设计技巧
在这一章内我们将集中讨论用于求解问题的 5 中常见类型的算法。对于许多问题,很可能这些方法中至少一种方法是考研解决问题的。特别地,对于每种类型的算法我们将:
- 看到一般的处理方法。
- 考查几个例子。
- 在适当的地方概括地讨论时间和空间复杂度。
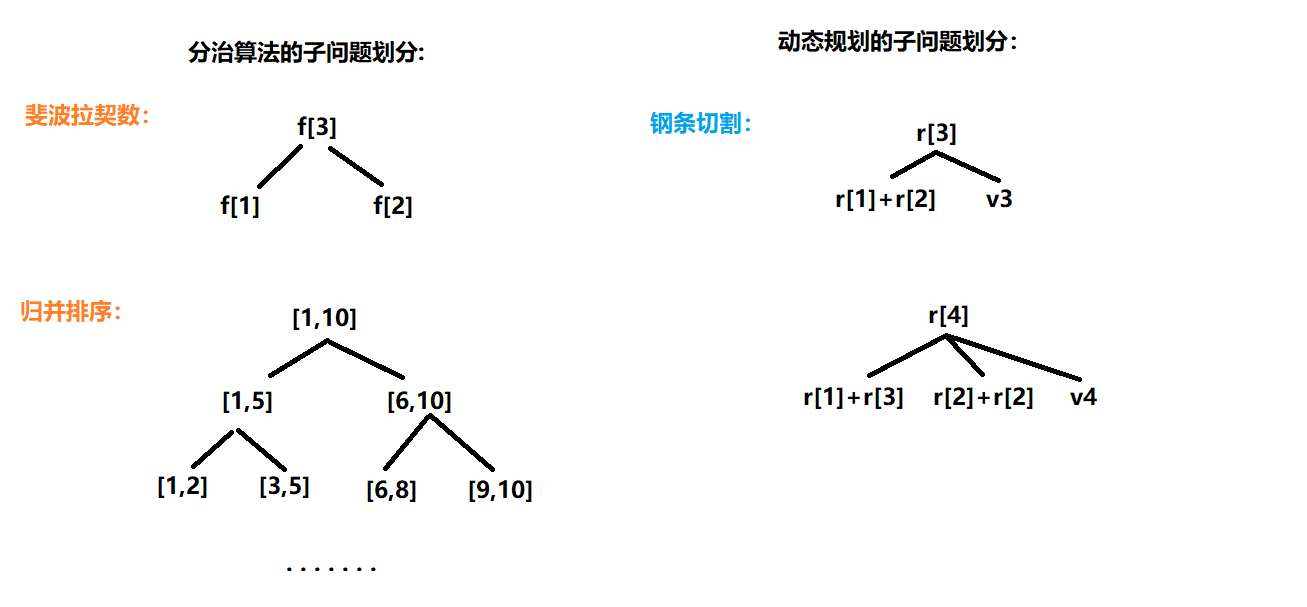
4.1、分治策略(Divide-and-Conquer)
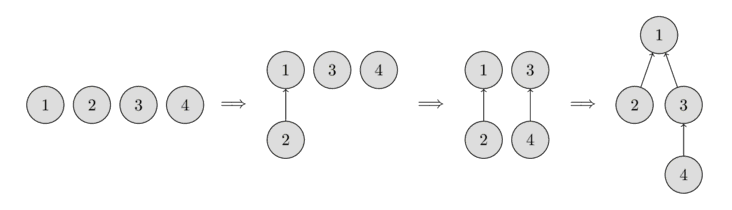
有许多有用的算法在结构上是递归的:为了解决一个给定的问题,算法一次或多次递归地调用其自身以解决紧密相关的若干子问题。以归并排序为例子,我们想要把整个数组变为一个有序数组,这是我们最初的原问题,他的子问题是什么呢?
我们将原问题设为 [1,n] 的数组排序,那么我们将子问题划分为对同一数组的 [1,mid],[mid+1,n] (mid = (1+n)/2) 这两部分使它成为有序数组。然后继续对这两个部分进一步的划分为子问题。在对一个子数组的排序过程,我们都采用同一种策略,这便是递归地调用其自身以解决紧密相关的若干子问题。
分治模式在每层递归时都有三个步骤:
- 分解原问题为若干子问题,这些子问题都是原问题的规模较小的实例(分解到不可再分的基问题,也就是递归的边界)。
- 解决这些子问题,递归地求解各子问题。然而,若子问题的规模足够小,则直接求解。
- 合并这些子问题的解成原问题的解。
一般的分治算法都将会遵循这个步骤编写代码(以归并排序为例)
当子问题足够大,需要递归求解时,我们称之为 递归情况 。当子问题变得足够小,不再需要递归时,我们说递归已经 触底,进入了基本情况。
传统上,在其代码中至少含有两个递归调用的例程叫作分治算法,而代码中只含一个递归调用的例程不是分治算法。我们一般坚持子问题是不相交的。比如我们在归并排序中第一次划分为 [1.mid]与[mid+1,n] 划分为了两个不重叠的子问题,以后的问题划分都是划分为不相交的子问题。
可用分治算法解决的问题
(1)二分搜索
(2)大整数乘法
(3)Strassen矩阵乘法
(4)棋盘覆盖
(5)归并排序
(6)快速排序
(7)线性时间选择
(8)最接近点对问题
(9)循环赛日程表
(10)汉诺塔
...
总结:
- 分治的三个步骤:
分解,解决,合并- 子问题分为大的子问题(需要继续递归处理进一步分解),小的子问题(不能再分已触底的问题,用最基本的方式来处理这个问题)。
- 分治的特性是自己调用自己,即可以用同样的方式处理规模不同的一类问题。
- 一个问题划分成为若干个不相交的子问题。
4.1.1、最大子数组
在数组 中寻找和最大的非空连续子数组
暴力算法
对于一段 天的日期,我们需要检查 个子数组,分别求和比较其值,求和的过程可以用前缀和数组来优化到 的初始化,每一次查询是 的,依然是 的算法。
使用分治策略的求解方法
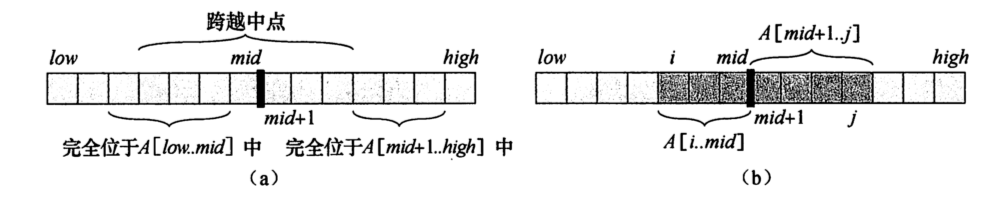
使用分治策略意味着我们要将子数组划分为两个规模尽量相等的子数组。也就是说,找到子数组的中央位置 ,考虑求解两个子数组 。 的所有连续子数组所处的位置必然属于下面三种情况之一:
- 完全位于 中
- 完全位于 中
- 跨越了中点的子数组。
所以,最大子数组也只会属于这三种情况之一。前两种情况可以递归的求解。
对于第三种情况,对于左边的数组,右端点一定是 ,左端点为 到 其中的任意一个数,我们直接从 遍历到 取最大值就好了。对于右边也是同样的情况。
4.1.2、最近点问题
这里,第一个问题的输入是平面上的点集 P。如果 和 ,那么 和 间的欧几里得距离为 。我们需要找出一对最近的点。有可能两个点位于相同的位置。在这种情形下这两个点就是最近的,它们的距离为零。
画出一个小的样本点集 。这些点已按 坐标排序(),我们可以画一条想象的垂线,把点集分成两半: 和 。现在得到的情形几乎和我们在上一节的最大子数组问题中见过的情形完全一样。
最近的一对点或者都在 中或都在 中,或者一个点在 中一个点在 中。我们把这三个距离分别叫做
4.2、动态规划(Dynamic Programming)
动态规划通常用来解决最优化问题,在这类问题中,我们通过做出一组选择来达到最优解。在做出每个选择的同时,通常会生成与原问题形式相同的子问题。当多余一个选择子集都生成相同的子问题时 (例如斐波拉契数不停的计算F[1],F[2]等),动态规划技术通常就会很有效,其关键技术是对每个这样的子问题都保存其解,当其重复出现时即可避免重复求解。
动态规划 Dynamic Programming 与分治方法相似,都是通过组合子问题的解来求解原题(这里,Programming 指的是一种表格法,并非编写计算机程序)。与分治的问题划分方法将问题划分为互不相交的子问题不同的是,动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题(子问题的求解是递归进行的,将其划分为更小的子子问题)。
在这种情况下,分治算法会做许多不必要的工作,它会反复地求解那些公共子子问题。而动态规划算法对每个子子问题只求解一次,将其保留在一个表格中,从而无需每次求解一个子子问题时都要重新计算,避免了这种不必要的计算工作。这样的表格将递归算法重新写成非递归算法。
我们以求 斐波拉契 数来举例说明。以下是用传统的分治法求斐波拉契数,有基本子问题的处理,以及子问题的划分以及解决。
如果我们画出递归树,我们将看到,每一个 fib() 函数都会反复地求解 fib[1] 的值。
F[1]的值被求了 8 次,F[2] 的值被求了 5 次等等。这就是前文所提到的 分治算法会做许多不必要的工作,它会反复地求解那些公共子子问题 。
以下是用数表的思想记录下每次求的值
其对应的求解流程为:
对比来可以看到,将求过的数存下来,并 自底向上 的求解问题这一思路将会避免重复求解已求过的数。当然这也有递归的版本:
这个版本的代码是自上而下的。
朴素递归算法值所以效率很低,是因为它反复求解相同的子问题。因此,动态规划方法仔细安排求解顺序(通常来说是自下而上满足拓扑序的),对每个子问题只求解一次,并将结果保存下来。如果随后再次需要此子问题的解,只需查找保存的结果而不必重新计算。
因此、动态规划的方法是付出额外的内容空间来节省计算时间,是典型的时空权衡的例子。而时间上的节省可能是非常巨大的。
动态规划方法通常用来求解最优化问题(optimization problem)。这类问题可以有很多可行解,每个解都有一个值,我们希望寻找具有最优值的解。我们称这样的解为问题的一个最优解,而不是最优解,因为可以有多个解都达到最优值。
我们通常按照如下 4 个步骤来设计一个动态规划算法:
- 刻画一个最优解的结构特征
- 递归地定义最优解的值
- 计算最优解的值,通常采用自底向上的方法
- 利用计算出的信息构造一个最优解
4.2.1、动态规划原理
适合应用动态规划的方法求解的最优化问题应该具备的两个要素:最优子结构和子问题重叠问题。
4.2.1.1、最优子结构(Optimal Substructure)
用动态规划方法求解最优化问题的第一步就是刻画最优解的结构。
如果一个问题的最优解包含其子问题的最优解,我们就称此问题具有 最优子结构 的性质。因此,某个问题是否适合应用动态规划算法,它是否具有最优子结构性质是一个好索引(当然,具有最优子结构性质也可能意味着适合应用贪心策略)。
对
一个问题的最优解包含其子问题的最优解的例子在钢条切割问题(描述见下文)中:
的所有子问题可以划分为( 是题目中给出的每一段的价值)
的值的求解会用到他的子问题 以及 ,这就是一个问题的最优解包含其子问题的最优解
使用动态规划方法时,我用子问题的最优解来构造原问题的最优解。因此,我们必须小心确保,原问题的最优解中所用到子问题的解,都是已确定的最优解。
对于子问题划分的进一步解释:
现在遇到过的分治算法一般来说划分的子问题都是确定好的,而动态规划中的子问题划分一般来说是变动的,但是会覆盖到所有的情况。
发掘最优子结构性质的过程中,实际上遵循了如下的通用模式:
- 证明问题的最优解的第一个组成部分是做出一个选择。做出这次选择会产生一个或多个待解的子问题。(在钢条切割中就为选择一个把钢条分成两部分的位置,或者不分割)
- 对于一个给定问题,在其可能的第一步选择中,你假定已经知道那种选择才会得到最优解。你现在并不关心这种选择具体是如何得到的,只是假定以及知道了这种选择。(对于 或 我们先假定它就是最优的子问题的解)
- 给定可获得最优解的选择后,你确定这次选择会产生那些子问题,以及如何最好地刻画子问题空间。
对于不同问题领域,最优子结构的不同体现在两个方面:
- 原问题的最优解中涉及多少个子问题
- 在确定最优解使用那些子问题事,我们需要考察多少中选择。
在钢条切割问题中,长度为 的钢条的最优切割方案仅仅使用一个子问题(长度为 的钢条的最优切割),但是我们必须考察 的 种不同的取值,才确定哪一个会产生最优解。
在动态规划方法中,我们通常自底向上地使用最优子结构。也就是说,首先求得子问题的最优解,然后求原问题的最优解。在求解原问题过程中,我们需要在涉及的子问题中做出选择,选出能得到原问题最优解的子问题。原问题最优解的代价通常就是子问题最优解的代价加上由此次选择直接产生的代价。
例如,对于钢条切割问题,我们首先求解子问题,确定长度为 的钢条的最优切割方案,然后利用公式确定那个子问题的解构成长度为 的钢条的最优切割方案。
后面我们会介绍的贪心算法,其和动态规划算法最大的不同在于,它并不是首先寻找子问题的最优解,然后在其中进行选择,而是首先做出一次 贪心 的选择——在当时(局部)看来最优的选择——然后求解选出的子问题,从而不必费心求解所有可能相关的子问题,在某种情况下这一策略也能得到最优解。
在钢条切割问题中就好比,我们在 1 这一步 (做出一个选择 )的时候我们就假定有一个切割方式就是全局最优的,而不用再考察其他的切割方案。
4.2.1.2、重叠子问题(Oberlapping SubProblem)
适合用动态规划方法求解的最优化问题应该具备的第二个性质是子问题的空间足够 小,即问题的递归算法会反复地求解相同的子问题,而不是一直生成新的子问题。如果递归算法反复求解相同的子问题,我们就称最优化问题具有 重叠子问题 的性质。
在
斐波拉契数的求解中,我们最初的代码就在不停的求解F[1],F[2]等等。
与之相对的,适合用分治方法求解的问题通常在递归的每一步都生成全新的子问题。动态规划算法通常这样利用重叠子问题性质:对每个子问题求解一次,将解存入一个表中,当再次需要这个子问题时直接查表,每次查表的代价为常量时间。
自顶向下的递归算法(无备忘)与自底向上的动态规划算法进行比较,后者要高效得多,因为它利用了重叠子问题性质。动态规划算法对每个子问题只求解一次。而递归算法则相反,对每个子问题,每当在递归树中(递归调用时)遇到它,都要重新计算一次。凡是一个问题的自然递归算法的递归调用树中反复出现相同的子问题,而不同子问题的总数很少时,动态规划的方法都能提高效率。
4.2.1.3、解决一个动态规划问题的步骤
- 识别出这是一个动态规划问题。
- 用最少的参数来具象化一个状态。
- 制定状态之间的转移关系
- 用表或记忆化的方式处理问题。
总结:
- 动态规划用于求解最优化问题。
- 动态规划的核心思想是用数表来存储之前求过的子问题的最优解。
- 动态规划的两个最重要的性质是:原问题的最优解包含子问题的最优解(即最优子结构),以及重叠子问题。
- 分析原问题与子问题的关系可以得到状态转移方程
- 分析状态转移方程,我们可以得到如何转移这个状态,使得在考察原问题时,所有的子问题都已被计算过。
4.2.2、线性动态规划
4.2.2.1、钢条切割
公司购买的长钢条,将其切割为短钢条出售。切割工序没有成本支出。公司管理层希望知道最佳的切割方案。以下是价格样表:
| 长度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 价格 | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
给定一段长度为 英寸的钢条和一个价格表 ,求切割钢条方案,使得销售收益 最大。
递归版本(没有使用动态规划的思想)
自顶向下动态规划
自底向上动态规划
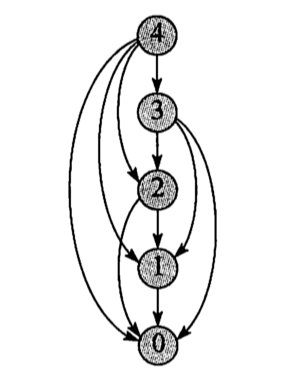
4.2.2.1.1、子问题图
当思考一个动态规划问题时,我们应该弄清所涉及的子问题与子问题的之间的依赖关系。
问题的子问题图准确地表达了这些信息。下图显示了 时钢条切割问题的子问题图。
它一个有向图,每个顶点唯一地对应一个子问题。若求子问题 的最优解时需要直接用到子问题 的最优解,那么在子问题图中就会有一条从子问题 的顶点到子问题 的顶点的有向边。
自底向上动态规划算法是按
逆拓扑序来处理子问题图中的顶点。换句话说,对于任何子问题,直至它因爱的所有子问题均已求解完成,才会求解它。
同样可以用
深度优先搜索来描述(带备忘机制记忆化搜索) 自顶向下动态规划算法处理子问题图的顺序。
通常,一个子问题的求解时间与子问题图中对应顶点的出度成正比,而子问题的数目等于子问题图的顶点数。因此,通常情况下,动态规划算法的运行时间与顶点和边的数量呈线性关系。
4.2.2.1.2、重构解(路径记录)
前文给出的钢条切割问题的动态规划算法返回最优解的收益,但并为返回解本身(一个长度列表,给出切割后每段钢条的长度)。我们可以扩展动态规划算法,使之对每个子问题不仅仅保存最优收益值,还保存对应的切割方案。利用这些信息,我们就能输出最优解。
使用
record数组记录这次选择的是那个
4.2.2.2、背包模型
4.2.2.2.1、01背包
有 件物品和一个容量是 的背包。每件物品只能使用一次。
第 件物品的体积是 ,价值是 。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
我最开始想的子问题是一维的,如钢条切割一样设为 来表示背包容量为 时的最优解,然后就发现无法解决这个问题,怎么都无法解决只选一个的问题。
之后看了题解之后,才考虑的把状态划分为二维的。
我们将原问题表示为 个物品,容量为 的背包,他的子问题有: 个物品,容量为 的背包, 个物品,容量为 的背包等等。 个物品,容量为 的最优解是从 个物品,容量为 的所有子问题中得到的。但是到底选哪个是取决于第 个物品的体积 。
由于下一个物品的体积的值有很多的情况,所以我们要把之前的所有物品的选择情况对应的所有背包容量的值都求出来也就是 。这样的话我们在求 的时候才能找到对应的值。
4.2.2.2.2、完全背包
完全背包问题相对于 01背包 还要简单点,因为物品的个数有无数多个。
我们的问题就只用考虑对于容量为 的背包,他能存放的最大价值是什么。
容量每 +1 我们都试着把所有物品再放一遍。
4.2.2.3、最长公共子序列
4.2.2.4、最长单调递增子序列
朴素最长公共子序列
由之前的思路我们首先建立原问题:以 结尾的最长上升子序列的长度为多少。
分析原问题与子问题的关系。 可以得出在前 的序列中,任何小于 的数都可以使 接在它的后面,形成一个新的最长上升子序列。小于 的数它自己本身就是一个最长上升子序列的结尾元素。
对于 的这样一个序列,我们考虑 的它可能构成的最长上升子序列有:
- 以 结尾的最长上升子序列(1)
- 以 结尾的最长上升子序列(1,8)
- 以 结尾的最长上升子序列(1,6)
- 以 结尾的最长上升子序列(1,5)
- 以 结尾的最长上升子序列(1,2)
我们以 来表示以 结尾的最长上升子序列的长度为多少。那么
这样我们就把状态转移方程列出来了。
转移的思路就是,我们遍历前面的所有子问题,如果当前这个数接到这个子序列的后面那么新的子序列的长度是多少,其最大值就是我们要求的最优解。我们从数组的前向后遍历,这样可以保证当前需要考察的所有子问题都是在之前就求解过的。
二分优化最长上升子序列
这个版本的原问题与之前的有所不同,我们设 表示 中最长上升子序列的长度(这就是我们最终想要的答案,也就是 dp[n] 就是最终答案),再用一个辅助数组 来表示当前长度为 的最长上升子序列中,第 位的最小值是多少。
对
cnt数组的进一步解释比如,对于数组
[1,7,3]:遍历到 时, ,
遍历到 时, ,
遍历到 时,由于
[1,3]新成了新的上升序列,且 ,则我们更新 。由最长上升子序列的特性,我们可以分析出
cnt数组一定是一个递增的有序数组。
我们的更新策略是:
- 如果 比当前的最长上升子序列的末尾元素还要大,那么我们就把它接到末尾,并更新 数组的值
- 如果 不满足
1的条件,那么我们在cnt数组进行二分找到第一个大于 的数的位置并替换他。
对
2的解释:对数组
[1,7,3,4]上一个解释中我们已经说到了
cnt[2]的值由,7变到了3,如果不进行这个变化下一个数4是无法扩展到cnt[3]的,也就是说,降低了形成新的最长上升子序列的门槛。
这个策略其实已经有点脱离动态规划的初心了,但仅仅是作为一个时间复杂度的优化的话,它是合格的。它更像一个贪心的思路,更新 cnt 数组虽然不能达到当前的最优解,但是能达到全局的最优解。
4.2.3、区间动态规划
区间动态规划,顾名思义其原问题的设置与区间有关,主要用来处理区间合并将会产生的代价问题。
状态数组 用来表示区间 [i,j] 处理后的一个最优代价,可能是最小值,可能是最大值等等。
石子合并
在一个环上有 个数 ,进行 次合并操作,每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
分析原问题与子问题的关系:
由于 [1,10] 的合并肯定是最后一个合并了,只会剩下两个石子了,但是这两个石子可能是由不同的合并情况得来的,且每次合并都只能合并相邻的石子,我们用区间来表示一种合并决策的最终情况。
比如区间 [2,10] 就表示这个区间内的所有石子已经合并为一个了,此时合并的最小代价。
考虑 [1,10] 区间的合并,一共有 种合并的方式,dp[1][1] 表示 [1,1] 整个区间合并的最小代价, dp[2][10] 代表 [2,10] 整个区间合并的最小代价(一个类似于原问题的子问题)。
上面为了使大家对区间有个直观认识画了框,下面为了表示所有情况,我们就直接用区间来代替。我们考察 [1,4] 这个区间的合并的所有情况:
这里展示了所有的合并情况,我们可以看到要想求长度为 的区间的合并,必须先求出长度为 所有区间的合并情况。这也是我们遍历的方式。我们也可以写出最终的状态转移方程:
(这里 cost 为两个区间合并的代价,即区间的质量和)
下面我们来讨论如何自下而上的求问题:
- 我们刚才也得出,首先应当以长度为第一个遍历点。
- 然后我们可以采用枚举区间左端点的方式来进一步确定这个大区间。
通过这两步,我们就已经能枚举出来处理的区间了。
下一个问题就是如何处理这个区间的最小代价的问题。我们看到上图的 [1,4],我们可以看到对于一个长度为 的区间,我们要比较三个部分。这三个部分分别以 作为断点,将区间划分为两个部分(这也是因为题目中只能合并两个相邻的区间这一性质得出来的)。
所以我们的转移方式就是枚举断点,这样就形成了一个三重循环。
到此,我们分析出了转移方程,以及转移方式可以开始写代码了。
看代码的时候结合上面
[1,4]图理解效果更好。
4.2.4、数位DP
基本原理:
考虑人类计数的方式,最朴素的计数就是从小到大开始依次加一。但我们发现对于位数比较多的数,这样的过程中有许多重复的部分。例如从 到 ,从 到 和从 到 的过程非常相似,它们都是后三位从 变到 ,不一样的地方只有千位这一位,所以我们可以把这些过程归并起来,将这些过程中产生的计数答案也都存在一个通用的数组里。此数组根据题目具体要求设置状态,用递推或 DP 的方式进行状态转移。
数位DP 中通常会利用常规计数问题技巧,比如把一个区间内的答案拆成两部分相减,即
那么有了通用答案数组,接下来就是统计答案。统计答案可以选择记忆化搜索,也可以选择循环迭代递推。为了不重不漏地统计所有不超过上限的答案,要从高到低枚举每一位,再考虑每一位都可以填那些数字,最利用通用答案数组统计答案。
4.2.4.1、数字计数
给定两个整数 和 ,求 和 之间的所有数字中 的出现次数。例如,,,则 和 之间共有 个数如下:
1024 1025 1026 1027 1028 1029 1030 1031 1032其中 出现 次, 出现 次, 出现 次, 出现 次等等…
如上文中提到的我们用前缀和的思想来求解问题,即,将问题 [a,b] 之间每一位中每个数字出现的次数,转化为求 [1,a-1],[1,b] 这两个区间中各自的每个数位出现的次数,然后用 [1,b] 中每一位的值减去 [1,a-1] 中每一位的值就是我们最终要求的答案。
在 ,, 这样的满 位(如 就是满 位的数 )的数中,每个数字出现的次数都是相同的。 中每个数字都出现了 次,在 中每个数字都出现了 次(这包含了前导 的情况,如 ,这样的 也是记录进去了的,我们最后再来单独处理前导 的情况)。对于这样的性质,设 dp[i] 表示满 位的数中,任意数字输出的次数。也就是说, 可以表示, 中 出现的次数,或者 出现的次数,他们的总次数都是相同的。可以归纳为公式:
对于递推公式的解释:
我们把一个数位分成两部分(
mi[i-1]为 )这里使用了动态规划最优子结构的性质,要求
dp[i]就得先求出 的值,我们将整个 位的值分为两个部分,前i-1位中某一个数字出现的次数(蓝色部分),第i位中某一次数字出现的次数,这两者的和构成我们总的dp[i]。为了方便叙述,我们假设 要求 ,中 一共出现了多少个(根据性质,每一个数字出现的次数都是一样的,所以我们随便选一个出来方便叙述)。
- 前 位中 一共出现了 次,也就是说,不论第 位取什么样的值,都会出现 次。然后,我们的第 位一共可以取 个数,所以第一部分的值就是 。这里可能不好理解,下图可能就比较直观了。
- 现在我们讨论第 位为 的情况。这种情况就比较简单,当且仅当第三位为 时,满足我们的条件。这样的数有 个,因为前两位的取值是从 一共 个也就是 (``500,501,···,599` 共 个)。
好,到此前期的准备工作我们已经做好了,接下来我们就要利用求出的 dp[i] 数组来得到 [1,a-1] 以及 [1,b] 中的每一个数位上数字出现的个数,其思路与我们上面的思路是类似的。
我们将会实现一个函数 solve() 用来求 中每个数位上的数字出现了多少次。
为了方便叙述,我们先解释每个数组代表的含义是什么。
a[]数组用来表示 的每一位是哪个数。mi[i]数组表示 的值。cnt[i]表示i这个数,一共出现了多少次,也就是我们想要得到答案。
还有一个需要进一步解释的地方就是 的满 位的数。
满 位的数为 : 0,1,2,3,4,5,6,7,8,9
满 位的数为 : 00,01,02,03,04,05,06,07,08,09,11,12,···,99
满 位的数为:001,002,003,004,005,006,007,008,009,010,011,···,999
可以看到我们会记录很多含有前导 的数,这也是为了方便讨论,我们最后会把这些数都去掉的。在计算满三位的数时,所有百位为 的数都是不合法的数,同理在计算满二位的数时,所有十位为 的数都是不合法的数。
在处理 位时,我们把 cnt[0] 减去 就可以了。
先不写后面的 solve函数了,还没有理解清楚
4.2.4.2、度的数量
求组合数的恒等式
原理是:我们把所有的方案分为两部分,包含第一个数的部分,以及不包含第一个数的部分。由于选了第一个数那么这部分的值为 ,另一部分由于一个数
我们将要考查的的第二种类型的算法是贪婪算法(greedy algorithm)。
贪婪算法分阶段地工作。在每一个阶段,可以认为所作决定是好的,而不考虑将来的后果。一般地说,这意味着选择的是某个局部的最优。这种眼下能拿就拿的策略即是这类算法名称的由来。当算法终止时,我们希望 局部最优等于全局最优。这种启发式策略并不保证总能找到最优解,但对于有些问题确实有效。
5、图论
5.1、基本图算法
本节将会介绍 图的表示 和 图的搜索。图的搜索指的是系统化地跟随图中的边来访问图中的每个结点。图搜索算法可以用来发现图的结构。许多的图算法在一开始都是会先通过搜索来获得图的结构,其他的一些图算法则是对基本的搜索加以优化。可以说,图的搜索技巧是整个图算法领域的核心。
5.2、最小生成树算法
5.3、单源最短路问题
5.4、所有结点对的最短路径问题
5.5、最大流
ACM技巧
与字符串处理有关的函数
与二进制有关的函数
进制转换
10进制数字转任意进制字符串
char * itoa ( int value, char * str, int base );
对于库函数 <stdlib.h> or <cstdlib> in c++
任意进制字符串转 10进制数
int stoi (const string& str, size_t* idx = 0, int base = 10);
算法库函数
STL
__EOF__

本文链接:https://www.cnblogs.com/hoppz/p/17152958.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
















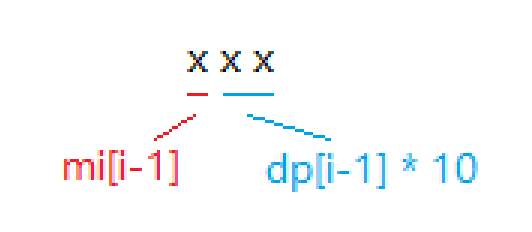



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 【杭电多校比赛记录】2025“钉耙编程”中国大学生算法设计春季联赛(1)