[ACM]树形结构基础 & 字典树
树形结构基础 & 字典树
1____树形结构基础
1.1____什么是树

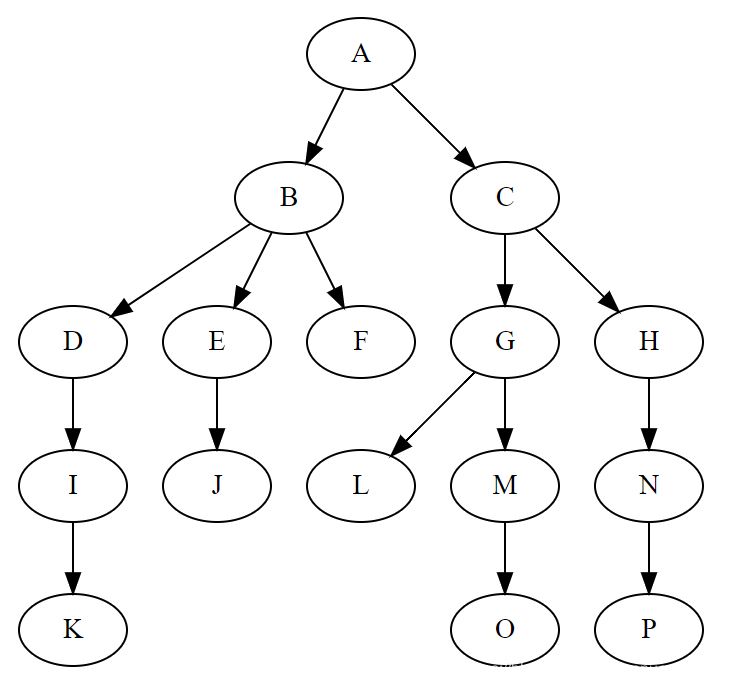
在现实世界层次化的数据模型中,数据与数据之间的关系纷繁复杂。其中很多关系无法使用简单的线性结构表示清楚,比如祖先与后代的关系、整体与部分的关系等。于是人们借鉴自然界中树的形象创造了一种强大的非线性结构——树。
现实中的树是由树根、茎干、树叶组成的,树的营养是由树根出发、通过茎干与树枝来不断优化传递,最终到达树叶的。在数据结构中,树则是用来概括这种传递关系的一种数据结构。为了简化,数据结构中把树枝分叉处、树叶、树根抽象为结点,其中树根树根抽象为根结点,且对于一棵树来说最多存在一个根结点;把树叶概括为叶子结点,且叶子结点不能再衍生出新的结点;把茎干和树枝统一抽象为边,且一条边只用来连接两个结点。
这样,树就被定义为由若干个结点和若干条边组成的数据结构,且在树中的结点不能被边连接成环。
每一个结点都可以看做一个新的根结点,由其组成的树成为子树。
对于树的定义还需要强调两点:
-
一棵树有且只有一个根节点。
-
子树之间不相交
1.2____树形结构的术语
-
结点:结点是树的基本构成单位,它由数据项及指向其他结点的分支(指针)共同组成。
-
度:树上任一节点所拥有的子节点的数目称为该节点的度,或度数。
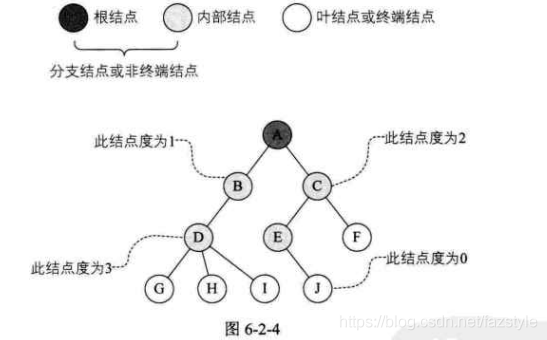
-
叶子节点:也称作终端结点,即度为0的结点。
-
分支结点(内部结点):也称作非终端结点,即度大于0的结点。
-
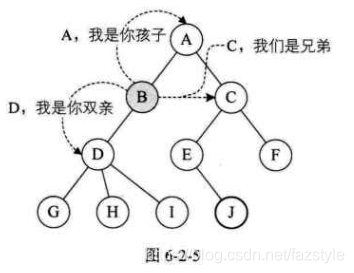
双亲结点(父结点):一个结点的直接前驱称为该结点的双亲结点。
-
子结点:如果结点A是结点B的父结点,那么结点B就是结点A的子结点。
-
兄弟结点:同一双亲结点的孩子结点间互称兄弟结点。
-
子孙结点:树中某一结点的所有子结点,以及这些子结点的子结点都是该结点的子孙结点。
-
祖先结点:若B是A的子孙结点,那么A即为B的祖先结点。
-
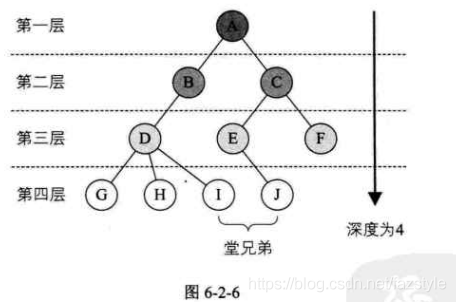
结点的层数:从根结点开始计算,根层数为0,其余结点的层数为其双亲的层数+1。
-
树的高度或深度:一颗树中所有结点层数的最大值。
-
森林:m(m>=0)个互不相交的树的集合,将一颗非空树的根结点删去,树就变成一个森林;给森林增加一个统一的根结点,森林就变成一棵树。
1.3____树的应用
-
操纵层次型数据结构
-
便于进行数据搜索
-
操纵已排序的数据列表
1.4____二叉树的定义
简明定义
对于这种在某个阶段都是两种结果的情形,比如开和关、0和1、真和假、上和下、对与错、正面和反面等,都适合用树状结构来建模,而这种树是很特殊的树状结构,叫做二叉树。
二叉树就是度不超过2的树,且两个子节点是有区别的(用此定义只是为了便于理解)
单纯的度不超过2的树与二叉树最大的区别就是,子结点是有区别的,是区分左右子树的。
递归定义
- 要么二叉树没有根结点,是一棵空树。
- 要么二叉树由根结点、左子树、右子树组成,且左子树和右子树都是二叉树。
递归定义就是用自身来定义自身。大家知道递归最重要的两个就是递归式和递归边界(结束条件),在二叉树的递归定义中1.就是递归边界,.2就是递归式。
二叉树中每一个结点及其子结点都可以看成一个完整且独立的二叉树,因此左子树和右子树也可以为空(.1),所以二叉树中每个结点最多有两个子女,即每个结点的度不超过2,且兄弟结点之间有左右子树之分,顺序不能颠倒。
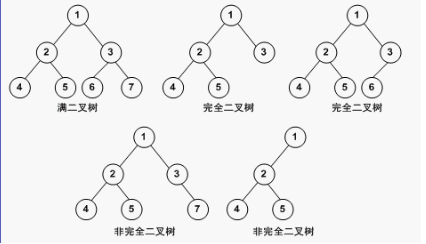
两种特殊的二叉树
-
满二叉树
(非人话)一棵深度为 k 且有 \(2^{k+1} - 1\) 个结点的二叉树。
(人话)每一层的结点个数都达到了当层能达到的最大结点数。
- 每一层上的结点数都达到了最大值。换言之,对于给定的高度,它是具有最多结点数的二叉树。
- 满二叉树中不存在度数为1的结点,即除了叶子结点度数为0外,其他结点的度数都为2。满二叉树的每个分支均有两个高度相同的子树。
-
完全二叉树
叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。(注:满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树)
- 叶子节点仅在层次最大的两层出现。
- 最后一层的结点只能从左到右一个一个加上去。
1.5____二叉树的性质
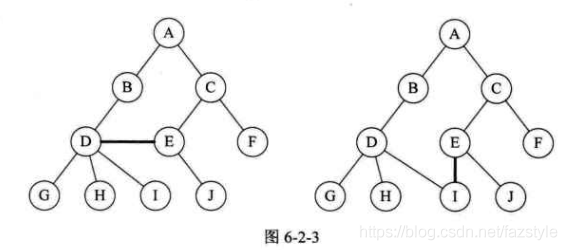
性质1: 即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。如下图,树1和树2是同一棵树,但它们却是不同的二叉树。
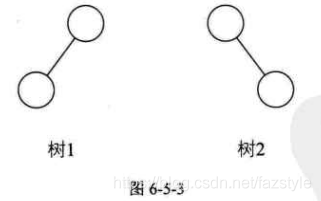
性质2: 对于非空二叉树,其第 i 层上的最大结点数目为 \(2^i\) ,其中 \(i \ge 0\)
性质3:深度为 k 的二叉树至多有 \(2^{k+1} -1\) 个结点,其中 \(k \ge -1\)。
(注:\(k = -1\) 时 结点个数为 0 这是表示这棵树为空树 )
性质4:在任意一棵非空二叉树中,若叶节点的个数为 \(n_0\) ,度为2的结点数为 \(n_2\),则 \(n_0 = n_2 + 1\)
性质5:具有 n 个结点的完全二叉树的深度为 \(k = [log_2(n+1)] -1\)
性质6:如将一棵有 n 个结点的完全二叉树自上向下,同一层自左向右连续赋予结点编号 \(1,2,3,..,n\),则对于任意下标为 i 的结点有:
(1) i = 1 ,则 i 是各节点,无父节点;若 \(i > 0\) 则其的父结点下标为 $ [(i-1)/2]$
(2) 若 \(2 \times i < n\) ,则 ik 的左儿子为 $ 2 \times i $
(3) 若 \(2 \times i + 1 < n\) ,则 i 的右儿子为 $2 \times i+1 $
(4) 若 i 为偶数,且 \(i \ne 1\) 则其右兄弟为 $ i + 1$,反之为奇数,其左兄弟为 \(i - 1\)
1.6 ____二叉树的存储结构与基本操作
一般的二叉树用链表来定义和普通的链表的区别是,由于二叉树每个结点有两条出边,因此指针域变成了两个——分别指向左子树和右子树的根节点地址。如果某个子树不存在,则指向NULL。
/* 因为实现规则的不同,部分为伪代码 */
#include <bits/stdc++.h>
using namespace std;
typedef struct Node
{
int date;
struct Node *l_son;
struct Node *r_son;
Node():date(0),l_son(NULL),r_son(NULL){}
}node;
/// 新建结点
node* newNode(int val)
{
node* no = new node();
no->date = val;
return no;
}
void insert(node *root ,int x)
{
if( root == NULL ){
root = newNode(x);
return ;
}
///建树规则
if( ... ){
insert(root -> l_son , x );
}else{
insert(root -> r_son , x );
}
}
/// 更新、查找
void search(node* root,int x,int newdate)
{
if( root == NULL){
return ; /// 递归边界
}
if( root -> date == x){
root -> date = newdate;
return ;
}
search( root -> l_son , x , newdate );
search( root -> r_son , x , newdate );
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(0);
...
return 0;
}
例1
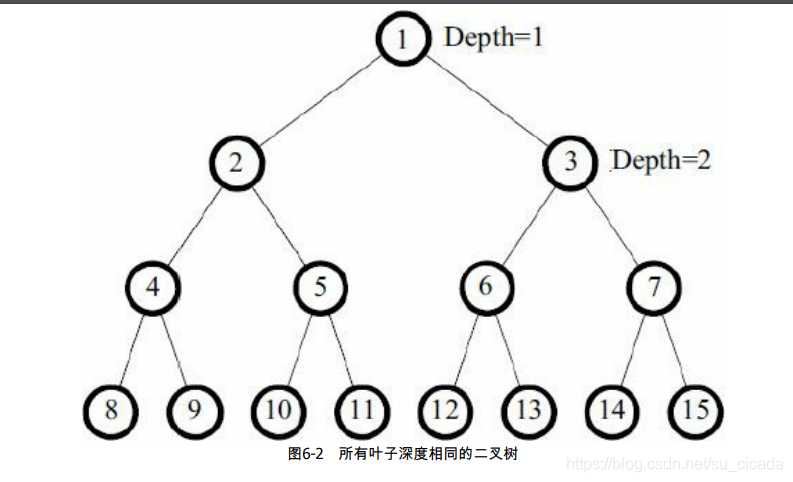
有一棵二叉树,最大深度为D,且所有叶子的深度都相同。所有结点从上到下从左到右
编号为\(1, 2, 3,…, 2^D-1\)。在结点 1 处放一个小球,它会往下落。每个内结点上都有一个开关,初始全部关闭,当每次有小球落到一个开关上时,状态都会改变。当小球到达一个内结点时,如果该结点上的开关关闭,则往左走,否则往右走,直到走到叶子结点,如图所示。
一些小球从结点1处依次开始下落,最后一个小球将会落到哪里呢?输入叶子深度D和
小球个数I,输出第I个小球最后所在的叶子编号。假设I不超过整棵树的叶子个数。D≤20。输入最多包含1000组数据。样例输入:
6 4 2 3 4 10 1 2 2 8 128 16 12345 -1样例输出:
12 7 512 3 255 36358
模拟
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
bool T[1<<N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(0);
int depth,n,k;
cin >> k;
while(k--){
cin >> depth >> n;
memset( T,0,sizeof T );
int k = 1, m = (1<<depth)-1;
for(int i = 0; i < n ; i++){
k = 1;
while(true){
T[k] = !T[k];
k = T[k]?(k<<1):(k<<1|1);
if(k > m) break;
}
}
/// 因为最后出界了,所以要除回来
cout << (k>>1) << "\n";
}
getchar();
return 0;
}
推规律
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(0);
int depth,n,m;
cin >> m;
while(m--){
cin >> depth >> n;
int k = 1;
for(int i = 0; i < depth - 1 ; i++){
if( n % 2){
k = k << 1;
n = (n + 1) >> 1;
}else{
k = (k << 1) + 1;
n >>= 1;
}
}
/// 因为最后出界了,所以要除回来
cout << k << "\n";
}
getchar();
return 0;
}
2____树上搜索
2.1____遍历
- 广度优先搜索:
(1)层次遍历
- 深度优先搜索:
(1)先序遍历
(2)中序遍历
(3)后序遍历
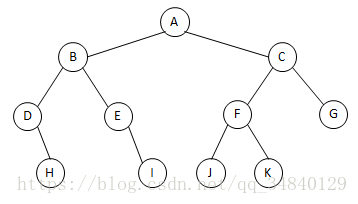
先序遍历(根左右):A B D H E I C F J K G
中序遍历(左根右) : D H B E I A J F K C G
后序遍历(左右根) : H D I E B J K F G C A
重点:每次在遍历一个结点的时候都把此结点看做一个棵以其作为根结点的完整的树。
递归实现
- 层序遍历
void LayerOrder(node* root)
{
queue<node*> q;
q.push( root );
while( !q.empty() ){
node* no =q.front();
q.pop();
cout << no -> date << endl;
if( now -> l_son != NULL ){
q.push( no -> l_son );
}else{
q.push( no -> r_son );
}
}
}
- 先序遍历
void preOrder(node* root)
{
if(root == NULL){
return ;
}
cout << root->date<<endl;
preOrder(root -> l_ron);
preOrder(root -> r_son);
}
- 中序遍历
void inOrder(node* root)
{
if( root == NULL ){
return ;
}
inOrder( root -> l_son );
cout << no -> daye << endl;
inOrder( root -> r_son );
}
- 后序遍历
void postOrder(node* root)
{
if( root == NULL ){
return ;
}
postOrder( root -> l_son );
postOrder( root -> r_son );
cout << no -> daye << endl;
}
2.2____ 先序与中序,后序与中序建树
从上一小节我们可以知道的结论:
- 先序遍历的第一个结点是根结点。
- 后序遍历的最后一个结点是根结点。
- 在中序遍历的结果中,知道根结点的位置后,它的左边就是他的左子树,它的右边就是他的右子树。
所以,知道一个树的中序 + (先序 || 后序)就可以确定一棵树,但是知道先序 + 后序则不行。
先序遍历:ABCDEFGHK
中序遍历:BDCAEHGKF
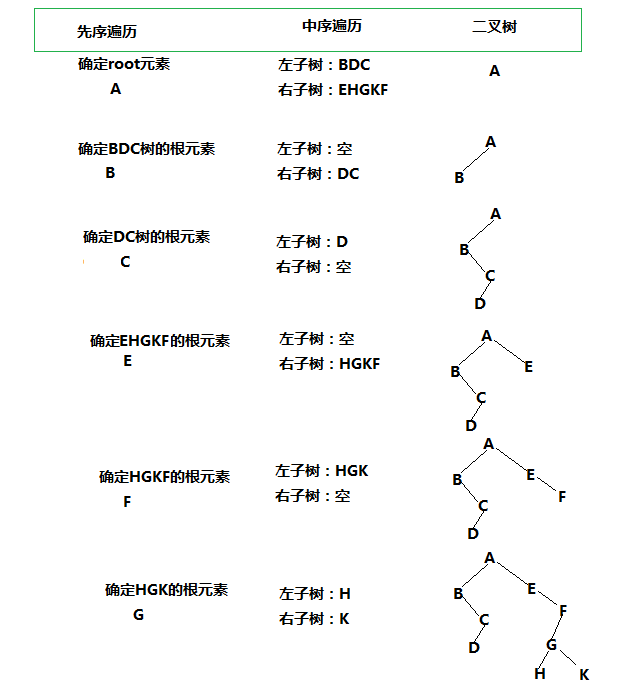
后序遍历:DCBHKGFEA
中序遍历:BDCAEHGKF

例2
Binary Tree Traversals - HDU 1710
输入二叉树的先序和中序遍历,求后序遍历
Input
n为输入数组的长度\(1 \le n \le 1000\)
有多组测试样例
Sample Input
9 1 2 4 7 3 5 8 9 6 4 7 2 1 8 5 9 3 6Sample Output
7 4 2 8 9 5 6 3 1
建树过程
(1)先序遍历的第一个数是整棵数的根结点,例如样例中的 1 。知道了 1 是根,对照中序遍历,1 左边的 4 7 2 都在根的左子树上,右边8 5 9 3 6都在根的右子树上。
(2)递归上述过程。例如,上面步骤得到中序遍历的4 7 2中,2左边的4 7 都在以2为根的左子树上,那么2是左子树的根,在中序遍历的4 7 2中,2左边的4 7都是在以2为根的左子树上,等等。
#include <bits/stdc++.h>
using namespace std;
typedef struct Node
{
struct Node *l_son;
struct Node *r_son;
int date;
Node():date(0),l_son(NULL),r_son(NULL){}
}node;
const int N = 2010;
int pre[N],in[N];
node *root = new node();
vector<int> vec;
node* create(int *pre,int *in,int n)
{
node *te;
/// 遍历 中序,在中序中找到先序的根节点
for(int i = 0; i < n ; i++){
if( pre[0] == in[i] ){ /// 说明在中序中匹配到根节点了
te = (node *) new node();
te -> date=in[i]; /// 此时可以确定的点就是当前这棵树的根节点。
te -> l_son = create( pre + 1 , in , i );
te -> r_son = create( pre + i + 1 , in + i + 1 , n - i - 1 );
return te;
}
}
return NULL; /// 如果没有子树了说明到了叶结点
/// 我们返回,将叶结点的左(右)子树赋值为NULL
}
void postOrder(node *root)
{
if( root == NULL ){
return ;
}
postOrder(root->l_son);
postOrder(root->r_son);
vec.push_back(root->date);
}
int main()
{
int n;
while( cin >> n ){
vec.clear();
for(int i = 0 ; i < n ; i++) cin >> pre[i];
for(int i = 0 ; i < n ; i++) cin >> in[i];
root = create(pre,in,n);
postOrder(root);
for(int i = 0 ; i < n ; i++){
cout << vec[i] << " \n"[i == n-1];
}
}
return 0;
}
3____字典树
我们来想想常见的字符串匹配问题:在 n 个字符串中查找某个字符串。
如果用暴力的方法,需要逐个匹配字符串,时间复杂度为 \(\Theta (n \times m)\),m是待匹配字符串平均长度。这个操作的效率是十分低下的。
还记得我们怎么查字典的吗?如果说我们要查找dog可以单词,是不是要先找到首字母为d的部分,然后再在这个部分里边查找o的部分,此时范围缩小到开头为do的单词了,所以再找到以g结尾的单词就好了。
字典树就是模拟解决这个过程的数据结构。
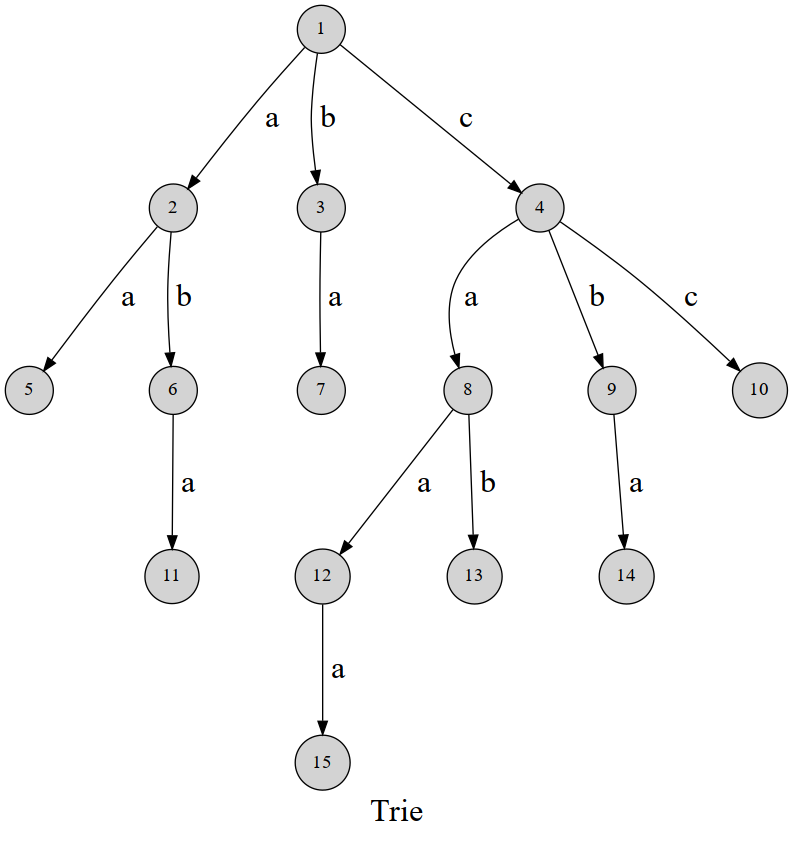
字典树的应用:
(1)字符串匹配。
(2)词频统计。
(3)字典序排序。(安装先序遍历,就是字典序了)
(4)前缀匹配。
例 3
Ignatius最近遇到一个难题,老师交给他很多单词(只有小写字母组成,不会有重复的单词出现),现在老师要他统计出以某个字符串为前缀的单词数量(单词本身也是自己的前缀).
Input
输入数据的第一部分是一张单词表,每行一个单词,单词的长度不超过10,它们代表的是老师交给Ignatius统计的单词,一个空行代表单词表的结束.第二部分是一连串的提问,每行一个提问,每个提问都是一个字符串.
注意:本题只有一组测试数据,处理到文件结束.
Output
对于每个提问,给出以该字符串为前缀的单词的数量.
Sample Input
banana band bee absolute acm ba b band abcSample Output
2 3 1 0
指针型树实现
#include <bits/stdc++.h>
using namespace std;
typedef struct Node
{
Node *next[26];
int num; /// 以当前字符串为前缀的数量
Node(){
for(int i = 0 ; i < 26; i ++) next[i] = NULL;
num = 0;
}
}tire;
tire root;
void insert(char *str)
{
tire *p = &root;
for(int i = 0 ; str[i] != '\0' ; i++){
if( p -> next[ str[i] - 'a' ] == NULL ){
p -> next[ str[i] - 'a' ] = new tire();
}
p = p -> next[ str[i] - 'a' ];
p -> num++;
}
}
void Find(char *str)
{
tire *p = &root;
for(int i = 0 ; str[i] != '\0' ; i++){
if( p -> next[ str[i] - 'a' ] == NULL ){
printf("0\n");
return ;
}
p = p -> next[ str[i] - 'a' ];
}
printf("%d\n",p -> num);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
char str[11];
while( gets(str) ){
if( !strlen(str) ) break;
insert( str );
}
while( gets(str) ){
Find(str);
}
return 0;
}
数组模拟
#include <bits/stdc++.h>
using namespace std;
const int N = 1000006;
int son[N][26],cnt[N],idx = 0;
void Insert(char *str,int len)
{
int p = 0;
for(int i = 0 ; i < len ; i++)
{
int u = str[i] - 'a';
if( !son[p][u] ) son[p][u] = ++idx;
p = son[p][u];
cnt[p]++;
}
}
int Query(char *str)
{
int len = strlen(str);
int p = 0,u;
for(int i = 0 ; i < len ; i++)
{
//cout << str[i] << ' ' <<c
u = str[i] - 'a';
if( !son[p][u] ) return 0;
p = son[p][u];
}
return cnt[p];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
char s[12];
while(gets(s))
{
int len =strlen(s);
if( len == 0) break;
Insert(s,len);
}
while( gets(s) )
{
cout << Query(s) <<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号