程序员必知8大排序3大查找
每天都在叫嚣自己会什么技术,什么框架,可否意识到你每天都在被这些新名词、新技术所迷惑,.NET、XML等等技术固然诱人,可是如果自己的基础不扎实,就像是在云里雾里行走一样,只能看到眼前,不能看到更远的地方。这些新鲜的技术掩盖了许多底层的原理,要想真正的学习技术还是走下云端,扎扎实实的把基础知识学好,有了这些基础,要掌握那些新技术也就很容易了。
要编写出优秀的代码同样要扎实的基础,如果排序和查找算法学的不好,怎么对程序的性能进行优化?废话不多说,本文要介绍的这些排序算法就是基础中的基础,程序员必知!
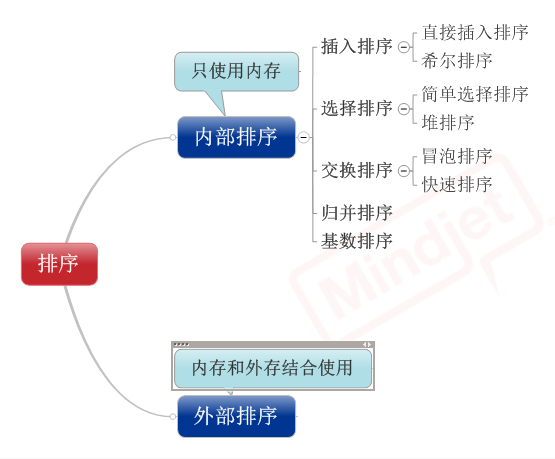
1、直接插入排序
(1)基本思想:在要排序的一组数中,假设前面(n-1) [n>=2] 个数已经是排
好顺序的,现在要把第n个数插到前面的有序数中,使得这n个数
也是排好顺序的。如此反复循环,直到全部排好顺序。
(2)实例
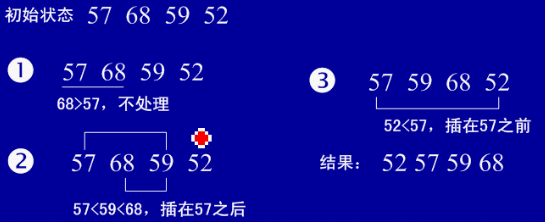
2、希尔排序(也称最小增量排序)
(1)基本思想:算法先将要排序的一组数按某个增量d(n/2,n为要排序数的个数)分成若干组,每组中记录的下标相差d.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。当增量减到1时,进行直接插入排序后,排序完成。
(2)实例:
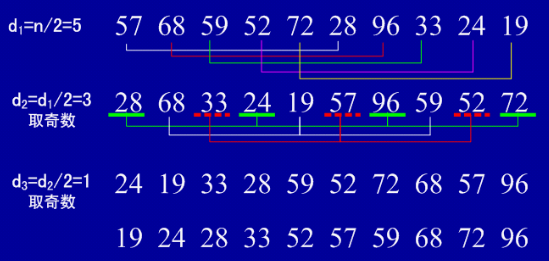
3、简单选择排序
(1)基本思想:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;
然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
(2)实例:

4、堆排序
(1)基本思想:堆排序是一种树形选择排序,是对直接选择排序的有效改进。
堆的定义如下:具有n个元素的序列(h1,h2,...,hn),当且仅当满足(hi>=h2i,hi>=2i+1)或(hi<=h2i,hi<=2i+1)(i=1,2,...,n/2)时称之为堆。在这里只讨论满足前者条件的堆。由堆的定义可以看出,堆顶元素(即第一个元素)必为最大项(大顶堆)。完全二叉树可以很直观地表示堆的结构。堆顶为根,其它为左子树、右子树。初始时把要排序的数的序列看作是一棵顺序存储的二叉树,调整它们的存储序,使之成为一个堆,这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推,直到只有两个节点的堆,并对它们作交换,最后得到有n个节点的有序序列。从算法描述来看,堆排序需要两个过程,一是建立堆,二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数,二是反复调用渗透函数实现排序的函数。
(2)实例:
初始序列:46,79,56,38,40,84
建堆:
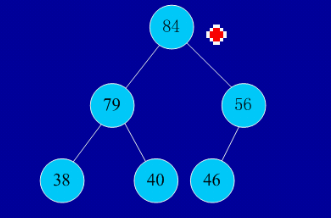
交换,从堆中踢出最大数

剩余结点再建堆,再交换踢出最大数

依次类推:最后堆中剩余的最后两个结点交换,踢出一个,排序完成。
5、冒泡排序
(1)基本思想:在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
(2)实例:

未完待续,第二篇将介绍剩余3大排序,排序稳定性,复杂度(这句话过期,呵呵!)
希望大家多多支持!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号