判断两条线段是否相交

之前一篇文章里写了一种差乘判断方法：http://www.cnblogs.com/hont/p/6105997.html

虽然用3D空间的差乘，但是只适用于2D空间

 

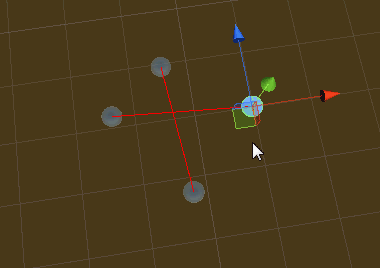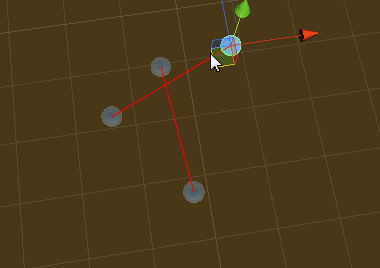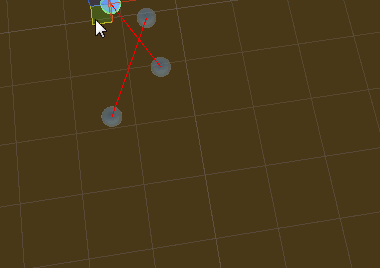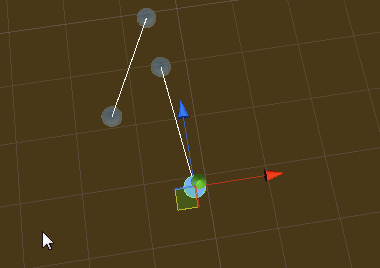
//线段ab与线段cd进行(Unity XZ空间)相交检测
bool IsIntersect(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
{
    var crossA = Vector3.Cross(d - c, a - c).y;
    var crossB = Vector3.Cross(d - c, b - c).y;

    if (!(crossA > 0f ^ crossB > 0f)) return false;

    var crossC = Vector3.Cross(b - a, c - a).y;
    var crossD = Vector3.Cross(b - a, d - a).y;

    if (!(crossC > 0f ^ crossD > 0f)) return false;

    return true;
}

 

 

后来我找到了另一个封装好的函数，不仅可以判断相交而且能查到是否相交于虚交点，是否平行等等。

原版的编写语言是java，但出处弄丢了

 

以下是我修改的Unity版本：

public static int GetIntersection(Vector3 a, Vector3 b, Vector3 c, Vector3 d, out Vector3 contractPoint)
{
    contractPoint = new Vector3(0, 0);

    if (Mathf.Abs(b.z - a.z) + Mathf.Abs(b.x - a.x) + Mathf.Abs(d.z - c.z)
            + Mathf.Abs(d.x - c.x) == 0)
    {
        if ((c.x - a.x) + (c.z - a.z) == 0)
        {
            //Debug.Log("ABCD是同一个点！");
        }
        else
        {
            //Debug.Log("AB是一个点，CD是一个点，且AC不同！");
        }
        return 0;
    }

    if (Mathf.Abs(b.z - a.z) + Mathf.Abs(b.x - a.x) == 0)
    {
        if ((a.x - d.x) * (c.z - d.z) - (a.z - d.z) * (c.x - d.x) == 0)
        {
            //Debug.Log("A、B是一个点，且在CD线段上！");
        }
        else
        {
            //Debug.Log("A、B是一个点，且不在CD线段上！");
        }
        return 0;
    }
    if (Mathf.Abs(d.z - c.z) + Mathf.Abs(d.x - c.x) == 0)
    {
        if ((d.x - b.x) * (a.z - b.z) - (d.z - b.z) * (a.x - b.x) == 0)
        {
            //Debug.Log("C、D是一个点，且在AB线段上！");
        }
        else
        {
            //Debug.Log("C、D是一个点，且不在AB线段上！");
        }
        return 0;
    }

    if ((b.z - a.z) * (c.x - d.x) - (b.x - a.x) * (c.z - d.z) == 0)
    {
        //Debug.Log("线段平行，无交点！");
        return 0;
    }

    contractPoint.x = ((b.x - a.x) * (c.x - d.x) * (c.z - a.z) -
            c.x * (b.x - a.x) * (c.z - d.z) + a.x * (b.z - a.z) * (c.x - d.x)) /
            ((b.z - a.z) * (c.x - d.x) - (b.x - a.x) * (c.z - d.z));
    contractPoint.z = ((b.z - a.z) * (c.z - d.z) * (c.x - a.x) - c.z
            * (b.z - a.z) * (c.x - d.x) + a.z * (b.x - a.x) * (c.z - d.z))
            / ((b.x - a.x) * (c.z - d.z) - (b.z - a.z) * (c.x - d.x));

    if ((contractPoint.x - a.x) * (contractPoint.x - b.x) <= 0
            && (contractPoint.x - c.x) * (contractPoint.x - d.x) <= 0
            && (contractPoint.z - a.z) * (contractPoint.z - b.z) <= 0
            && (contractPoint.z - c.z) * (contractPoint.z - d.z) <= 0)
    {

        //Debug.Log("线段相交于点(" + contractPoint.x + "," + contractPoint.z + ")！");
        return 1; // '相交  
    }
    else
    {
        //Debug.Log("线段相交于虚交点(" + contractPoint.x + "," + contractPoint.z + ")！");
        return -1; // '相交但不在线段上  
    }
}