文本指纹算法和内容指纹系统介绍
1. 文本指纹介绍
Web大量上的网页集合里存在大量的重复内容网页,无论对于搜索引擎的网页去重和过滤、新闻小说等内容网站的内容反盗版和追踪、还是社交媒体等文本去重和聚类,都需要对网页或者文本进行去重和过滤。
最简单的文本相似性计算方法可以利用空间向量模型,计算分词后的文本的特征向量的相似性,这种方法存在效率的严重弊端,无法针对海量的文本进行两两的相似性判断。模仿生物学指纹的特点,对每个文本构造一个指纹,来作为该文本的标识,从形式上来看指纹一般为固定长度较短的字符串,相同指纹的文本可以认为是相同文本。
最简单的指纹构造方式就是计算文本的md5或者sha哈希值,除非输入相同的文本,否则会发生“雪崩效应”,极小的文本差异通过md5或者sha计算出来的指纹就会不同(发生冲撞的概率极低),那么对于稍加改动的文本,计算出来的指纹也是不一样。
因此,一个好的指纹应该具备如下特点:
1. 指纹是确定性的,相同的文本的指纹是相同的;
2. 指纹越相似,文本相似性就越高;
3. 指纹生成和匹配效率高。
业界关于文本指纹去重的算法众多,如k-shingle算法、google提出的simhash算法、Minhash算法、top k最长句子签名算法等等,本文接下来将简单介绍各个算法以及指纹系统的基本架构和思路。
2. 常用的指纹算法
2.1 k-shingle算法
shingle在英文中表示相互覆盖的瓦片。对于一段文本,分词向量为[w1,w2, w3, w4, … wn], 设k=3,那么该文本的shingle向量表示为[(w1,w2,w3),(w2,w3,w4), (w3,w4,w5), …… (wn-2,wn-1,wn)],计算两个文本的shingle向量的相似度(jarccard系数)来判断文本是否重复。由于k-shingle算法的shingle向量空间巨大(特别是k特别大时),相比vsm更加耗费资源,一般业界很少采用这类算法。
2.2 Simhash算法
Simhash是google用来处理海量文本去重的算法,同时也是一种基于LSH(localitysensitive hashing)的算法。简答来说,和md5和sha哈希算法所不同,局部敏感哈希可以将相似的字符串hash得到相似的hash值,使得相似项会比不相似项更可能的hash到一个桶中,hash到同一个桶中的文档间成为候选对。这样就可以以接近线性的时间去解决相似性判断和去重问题。
simhash算法通过计算每个特征(关键词)的哈希值,并最终合并成一个特征值即指纹。
simhash算法流程
1. 首先基于传统的IR方法,将文章转换为一组加权的特征值构成的向量。
2. 初始化一个f维的向量V,其中每一个元素初始值为0。
3. 对于文章的特征向量集中的每一个特征,做如下计算:
a) 利用传统的hash算法映射到一个f-bit(一般设成32位或者64位)的签名。对于这个f- bit的签名,如果签名的第i位上为1,则对向量V中第i维加上这个特征的权值,否则对向量的第i维减去该特征的权值;
b) 整个特征向量集合迭代上述运算后,根据V中每一维向量的符号来确定生成的f-bit指纹的值,如果V的第i维为正数,则生成f-bit指纹的第i维为1,否则为0。

图1 simhash算法示意图
Simhash指纹匹配过程
经过simhash指纹生成算法生成的指纹是一个f位的二进制字符串,如一个32位的指纹,‘101001111100011010100011011011’。对于两个文本的f位0-1字符串,simhash算法采用hammingdistance来计算两个指纹之间的相似度,但是对于海量文本,如何从千万级别(甚至更多)的指纹集合中,找出最多只有k位不同的指纹呢?
一个简单的思想就是以空间换时间,对于一个32位的指纹来说,将该指纹划分成4段,即4个区间,每个区间8位,如果两个指纹至多存在3(设k=3)位差异,那么至少有一段的8位是完全相同的,因此可以考虑利用分段来建立索引,来减少需要匹配的候选指纹数量。
Simhash指纹匹配算法
1. 首先对于指纹集合Q构建多个表T1,T2…Tt,每一个表都是采用对应的置换函数π(i)将32-bit的fingerprint中的某p(i)位序列置换换到整个序列的最前面。即每个表存储都是整个Q的fingerprint的复制置换;
2. 对于给定的F,在每个Ti中进行匹配,寻找所有前pi位与F经过π(i)置换后的前pi位相同的fingerprint。
3. 对于所有在上一步中匹配到的置换后的fingerprint,计算其是否与π(i)(F)至多有k-bit不同。
Simhash算法比较高效,比较适用于对于长文本。
2.3 Minhash算法
Minhash也是一种LSH算法,同时也是一种降维的方法。Minhash算法的基本思想是使用一个随机的hash函数h(x)对集合A和B中的每个元素进行hash,hmin(A)、hmin(B)分别表示hash后集合A和集合B的最小值,那么P(hmin(A)== hmin(B)) = Jaccard(A, B)。这是minhash算法的核心,其中hmin(A)为哈希函数h(x)对集合A的最小哈希值。
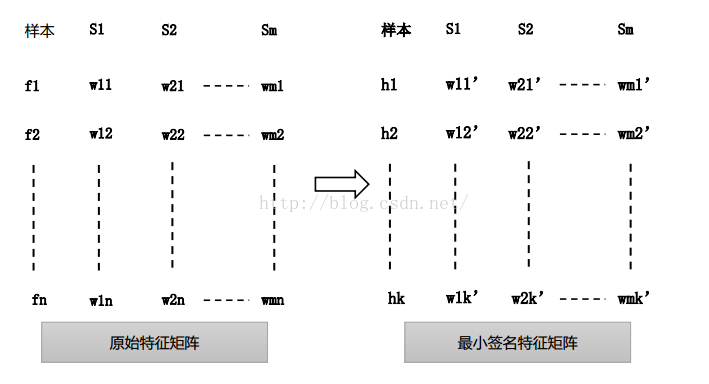
图: 最小签名矩阵生成示意图
Minhash算法采用最小哈希函数族(一组随机的最小哈希函数)来构建文档的最小哈希签名。文档的最小哈希签名矩阵是对原始特征矩阵降维的结果。应用过程中,可以使用k个最小函数分别计算出集合的哈希最小值。设hi表示第i个最小hash函数,最小签名矩阵中列向量为样本si的最小签名向量,其中wij表示第j个最小hash函数对样本i的最小哈希值。
当k小于原始集合的长度(k<< n)时,就相当于对数据降维,类比PCA等降维方法,minhash避免了复杂的矩阵运算。由于最小签名矩阵中,样本i,j的某一行或某几行的子向量的相似度于样本i,j的jarcarrd距离相等,因此可以对最小签名矩阵运行行条化策略,经矩阵平均分为b个行条,每个行条由r条组成,当两个样本在任意一个行条中的向量相等,即是一个相似性候选对,并检查文档是否真正相似或者相等。
关于minhash的原理和推导,以及在大量文本及高维特征下如何快速进行最小签名矩阵的构建操作可以参考https://en.wikipedia.org/wiki/MinHash及《大数据 互联网大规模数据挖掘与分布式处理》。(数学的奥妙就在于此)
经过minhash降维后的文本向量,从概率上保证了两个向量的相似度和降维前是一样的,结合LSH技术构建候选对可以大大减少空间规模,加快查找速度。
3. 内容型网页文本指纹算法
从前文可以看出,指纹识别算法是实现指纹识别的关键,它直接决定了识别率的高低,是指纹识别技术的核心。特别是类似新闻类、小说类网页在转载或者盗版过程中,文字的个数、顺序上一般都保持一致,当然不排除个别字错误或者少一个字的情况。
指纹生成的过程主要包括将文本全部转换成拼音、截取每个字拼音的首字母、统计该粒度内字母的频率分布、通过和参考系比较,将结果进行归一化、按字母序,将数字表征转换成数字。

图2 指纹生成算法
算法描述:
1. 转拼音:可以解决字符集编码不一致的问题,可以利用程度的英文指纹算法,减小分布空间,同时可以解决同音字替代问题;
2. 截取拼音首字:减小存储长度和分布空间(26个字母);
3. 提取首字母频率:选择多少字来计算指纹,统计频率分布。需要设置颗粒度的大小(分段大小)以及重叠率。
大粒度容错性高,但是匹配率低;小粒度容错性低,但是误报率高且敏感度高。
重叠率是设置指纹计算片段移动的窗口大小:
假设拼音内容长为2n,颗粒长度为n,重叠率为50%,则需要计算的指纹片段分别为[1-n],[n/2,3*n/2],[n,2n]
4. 减去参考系:频率减去参考系
5. 归一化:将每个字母的数字特征归一化到一个闭区间内,如[0,9],按照字母顺序连接数字特征,变成一个数字,即指纹。
• 若空间为[0,9],即一个20位的整数,2^64,需要 8 byte
• 若空间为[0,7],可用一个20位的8进制数,8^20,需要 8 byte
• 若空间为[0,3],只需要 4^20, 共40 bit, 5 byte
• 若空间为[0,1],需要2^20,20 bit,3 byte
归一化过程的算法步骤如下,假设颗粒长度为m:
输入:片段频率集合S:[s1,s2,s3,…sn]
参数:指纹集合dnas:[]
计算基数radix:=pow(2, log(m)/log(2) )
FOR 片段频率s IN S
修正频率,每个频率值:=max(频率,基数)
指纹dna:=空串
FOR tmp IN s[m-5:m]
将tmp转换成整数,基数为radix
将tmp转换成字符串,基数为radix
dna:=dna连接tmp
dnas:=dnas添加dna
END
输出:指纹集合dnas
4. 指纹系统结构
指纹追踪系统主要由爬虫系统、指纹生成系统、指纹存储、指纹查询和比对、数据分析、后台管理系统等几个主要模块构成。
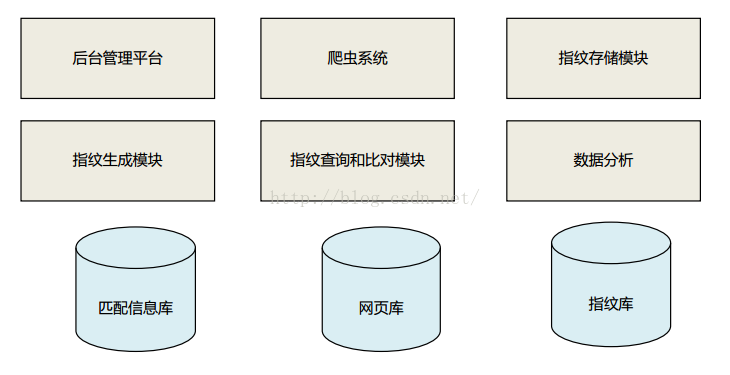
图3 指纹追踪系统模块图
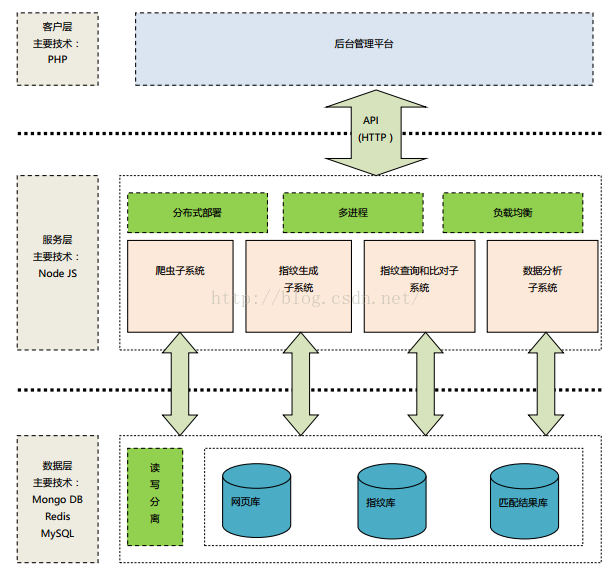
图4 系统架构图

图5 系统流程图
5. 总结
对于网页去重、内容盗版追踪、内容聚类等应用来说,指纹模块都是极其重要的模块。本文介绍了一些比较常用的指纹算法,包括k-shingle、simhash、minhash;同时介绍了指纹追踪系统及其关键算法,在实际的使用过程中,需要根据具体业务场景,确定具体的架构设计和应用算法。
————————————————
版权声明:本文为CSDN博主「wh_springer」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/wh_springer/article/details/52177236



