Convolutional Neural Networks（CNN）

数学基础

卷积

卷积这一概念从最原始来说属于一种数学的运算方法，两个数列进行卷积，是指将一个数列翻转后，从另一个数列最左侧开始滑动求和
来到计算机科学中，由于卷积核往往采用对称矩阵，所以翻转这一动作实际就可以忽略掉了。通过卷积核中数据的不同排列，实现提取出输入图片中的特定特征。

训练 + 预测

目前理解的是，预测仅需要实现正向传播那一堆层，得到预测概率
训练需要在实现正向传播基础上，得到预测概率后经过反向传播不断修正模型，所以难点在于反向传播

对于训练来说，需要考虑通过何种方法能够得到何时的卷积核
但对于预测来说，应当是建立在模型训练好的基础之上的，即已经获取到了模型参数（这个参数包含什么？）
我们需要知道采用何种卷积核，网络结构如何设置，难道这些数据都包含在训练好的模型提供的参数中了吗

神经网络中采用的各种参数究竟取多少，是期望使用神经网络预测物品的类型决定的，在训练过程中，反向传播帮助确定了各参数的值

卷积神经网络的层次划分

输入层，卷积层，激活层，池化层，全连接层，输出层

卷积层、池化层，全连接层被称为隐含层

输入层

输入层的作用是将输入数据送入卷积神经网络进行特征提取，然后获得我们想要的结果

卷积层（Convolutional Layer）

卷积层对输入数据进行特征提取，通过卷积核矩阵对原始数据中隐含关联性进行抽象

  • 局部连接（有助于减少参数量）
  • 权值共享

运算所用的数组 <=> 过滤器（filter）<=> 神经元（neuron） <=> 核（kernel）
卷积核每次覆盖的区域 <=> 感受野（receptive field）
卷积运算 <=> 卷积核在输入数据上的移动，过滤器中的值会与图像中的原始像素值相乘（又称为计算点积）的过程
卷积运算得到的数组 <=> 激活映射（activation map）或特征映射（feature map）

提取特征不过是用一些特殊的数组来同输入数据进行相乘，得到一个输出矩阵。不同的过滤器能够提取出原始图像中的不同特征，通过叠加多层过滤器，能够得到较为高级的激活映射

涉及到的参数

  1. 滤波器尺寸
  2. 步幅（stride）
  3. 填充（padding）
    每一次卷积，都会使得数据规模缩小，在网络的早期层中，我们想要尽可能多地保留原始输入内容的信息（减慢数据规模缩小的速度），这样我们就能提取出那些低层的特征。
    通过填充实现这一点，零填充在输入内容的边界周围补充零。

一个卷积层所需的过滤器的数量应当和图片通道数相等，若处理的是灰度图，仅有一个通道，所以一个卷积层仅需要一个过滤器，如果处理的是RGB图，一个卷积层就需要3个过滤器

激活层（非线形层）

卷积操作是把输入图像和卷积核进行相应的线性变换，引入激活层 (非线性函数) 对其进行非线性映射。
激活函数的意义在与两点：1.把数据限制在一定范围内 2.加入非线性因素，避免线性模型的表达力不足问题

常见激活函数

  • sigmoid
  • Tanh（双曲正切）
  • ReLU（Rectified Linear Unit）

池化层（pooling layer）(汇聚层 / 子采样层 / 下采样（downsampling）层)

将特征图下采用，作用是对感受域内的特征进行筛选，提取区域内最具代表性的特征，能够有效地降低输出特征尺度，进而减少模型所需要的参数量

常见类型

  • 最大池化：提取感受域内最大的特征值作为输出
    用不重叠的矩形框将输入层分成不同的区域，对于每个矩形框的数取最大值作为输出层

  • 平均池化：提取感受域内平均特征值作为输出

  • 求和池化：提取感受域内特征值总和作为输出

全连接层

将多维的特征输入映射为二维的特征输出

这一层处理输入内容（该输入可能是卷积层、ReLU 层或是池化层的输出）后会输出一个 N 维向量，N 是该程序必须选择的分类数量。例如，如果你想得到一个数字分类程序，如果有 10 个数字，N 就等于 10。这个 N 维向量中的每一数字都代表某一特定类别的概率。例如，如果某一数字分类程序的结果矢量是 [0 .1 .1 .75 0 0 0 0 0 .05]，则代表该图片有 10% 的概率是 1、10% 的概率是 2、75% 的概率是 3、还有 5% 的概率是 9（注：还有其他表现输出的方式，这里只展示了 softmax 的方法）

它通过将卷积层的特征进行合并或者取样，提取出其中的具有区分性的特征，从而达到分类的目的。

反向传播

反向传播可分为四部分，分别是前向传导、损失函数、后向传导，以及权重更新。

一个模型是如何进行训练的
初始状态下，权重或过滤器值都是随机的。滤波器不知道要去寻找边缘和曲线。更高层的过滤器值也不知道要去寻找爪子和鸟喙。
在第一个训练样例上，由于所有的权重或者过滤器值都是随机初始化的，输出可能会是 [.1 .1 .1 .1 .1 .1 .1 .1 .1 .1]，即一个不偏向任何数字的输出。一个有着这样权重的网络无法寻找低级特征，或者说是不能做出任何合理的分类。
误差的计算只需要选择一个误差计算函数，例如均方误差
然后梯度下降，调整参数

典型的卷积神经网络模型

LeNet-5

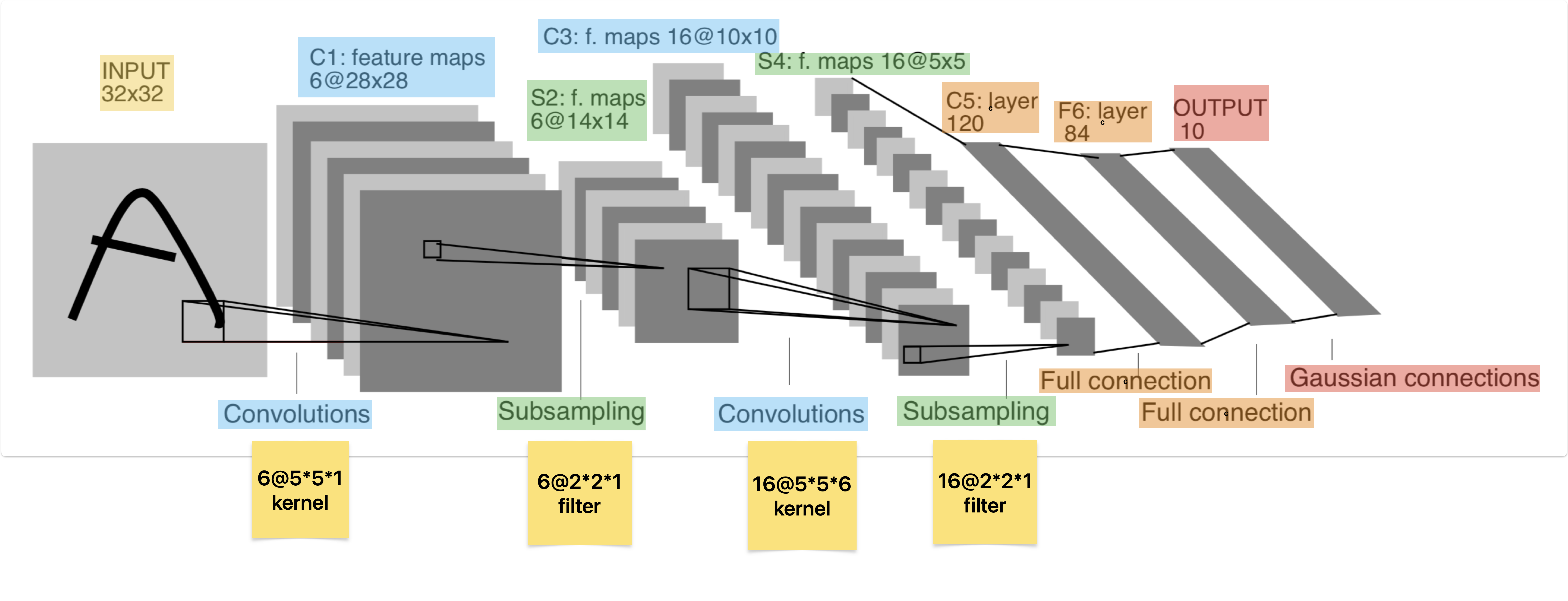
需要注意的是，在上图中从始至终我们处理的都只是一个输入，至于中间的多个feature map，那实际属于下一个环节的一个输入的多个通道，并不会在后续操作中就变为了多个输入（这一点理解会影响后续参数计算）

输出参数行数

bias weight
conv1 6 150
conv2 16 2400
fc1 120 30720
fc2 84 10080
fc3 10 840

在考虑以上参数都是如何计算得来之前，需要首先明确一下通道的概念
输入图片和卷积核都有4个属性：长度，宽度，通道数，个数
假设有一个28*28的RGB图片，它的长度是28，宽度是28，通道数是3，个数是1
一个能和该图片进行运算的卷积核，通道数必须也是3，对应通道的矩阵进行卷积运算，会得到3个矩阵，相加再加上一个bias矩阵得到输出

输入层通道数 = 卷积核通道数
卷积核个数 = 输出层通道数

实际从pytorch的函数参数也可以看出，在定义卷积层时，只需要提供输入通道数和输出通道数，给定输入通道数，就能够确定卷积核的通道数；给定输出通道数，就能够确定卷积核的个数

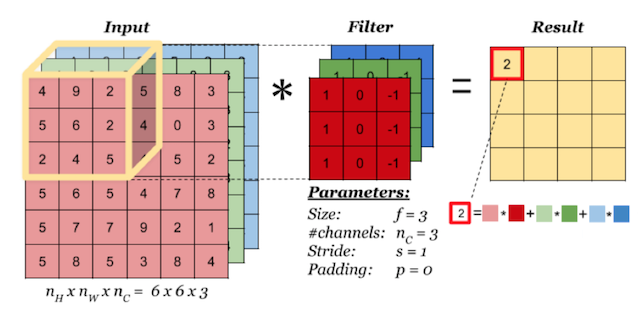
  1. 对于一个多通道输入和一个卷积核卷积，计算方法为，对应通道进行卷积，再把所有通道的卷积结果求和，这样得到的是一个单通道输出
    eg：一个（5，5，3）输入，一个卷积核（3，3，3），卷积结果是（5，5，1）
    假设用k表示通道数，实际的运算公式为
    input_k1 卷积 kernel_k1 +
    input_k2 卷积 kernel_k2 +
    input_k3 卷积 kernel_k3
    = output

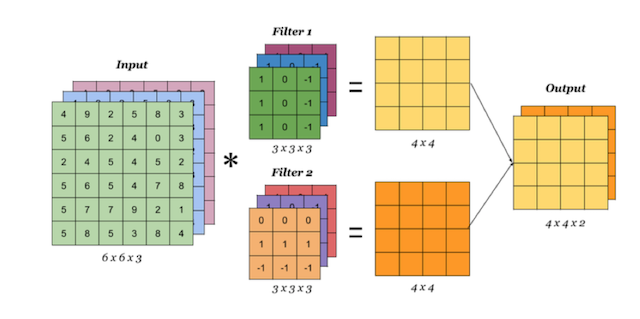
  1. 对于一个多通道输入和多个卷积核卷积，过程只不过是有几个卷积核，就进行几次“一个多通道输入和一个卷积核卷积”过程，
    和单个卷积核进行卷积得到一个单通道输出，因此有几个卷积核最终就可获得几通道输出

对于多个多通道输入，也只能是重复上述1和2的过程，完成多个“一个多通道输入和一个或多个卷积核卷积”过程
因为卷积操作只能接受单个输入和单个卷积核

激活层采用Relu 和 池化层采用最大池化 都是采用固定的模式，因此并不需要参数

  1. conv1:
    输入通道为1，输出通道为6，卷积核的尺寸定为了5*5
    输入通道数为1决定了卷积核的通道数为1，输出通道数为6决定了一共需要6个卷积核，即6个5*5*1个卷积核
    一个卷积核包含权重5*5*1=25个，6个卷积核一共25*5=150个weight
    偏移量的运算逻辑是，权重矩阵进行运算时，感受野内的数据和卷积核内的对应位置的数据计算乘积和，得到一个数据，需要把这个数据加上当前卷积核对应的偏移量。因此6个卷积核一共需要6个偏移量，即6个bias
    所以conv1一共包含156个参数

  2. conv2
    in_channel = 6, out_channel = 16, 卷积核的尺寸定为 5 * 5
    in_channel -> 卷积核in_channel = 6, out_channel -> 卷积核个数 = 16
    一个卷积核包含权重5*5*6=150个，16个卷积核一共150*16=2400个weight
    16个卷积核一共需要16个偏移量，即16个bias
    所以conv2一共包含2416个参数

  3. fc1
    fc1对应着从S4到C5进行的第1次线性运算，实际效果是把一个1*256的矩阵，通过矩阵乘法变为了1*120的矩阵
    weight实际是一个120*256（展开后一共30720个元素）的矩阵，bias是一个1*120的矩阵
    运算过程为weight * S4 + bias = C5

  4. fc2
    fc1对应着从C5到F6进行的第2次线性运算，实际效果是把一个1*120的矩阵，通过矩阵乘法变为了1*84的矩阵
    weight实际是一个84*120（展开后一共10080个元素）的矩阵，bias是一个1*84的矩阵
    运算过程为weight * C5 + bias =F6

  5. fc3
    fc1对应着从F6到output进行的第3次线性运算，实际效果是把一个1*84的矩阵，通过矩阵乘法变为了1*10的矩阵
    weight实际是一个10*84（展开后一共840个元素）的矩阵，bias是一个1*10的矩阵
    运算过程为weight * F6 + bias = output

全连接和高斯连接，从给出的利用pytorch代码来看，区别在于全连接在一个线性运算后，会跟一个激活函数，高斯连接仅做一个线性运算

具体实现

PyTorch torch.nn

torch.nn是一个专门为神经网络设计的模块化接口，包含了神经网络中涉及到的各种模块
可以借助它实现自定义的网络，例如 LeNet-5

C++ 实现CNN用于fashion-mnist

整体网络结构

10000张测试样本图存储在一个二维数组

Reference

posted @ 2023-10-11 13:36  0x7F  阅读(35)  评论(0)  编辑  收藏  举报