CSAPP-Data Lab

gcc -O1 -Wall -m32 -lm -o btest bits.c btest.c decl.c tests.c
In file included from btest.c:16:0:
/usr/include/stdio.h:27:10: fatal error: bits/libc-header-start.h: No such file or directory

include <bits/libc-header-start.h>

      ^~~~~~~~~~~~~~~~~~~~~~~~~~

compilation terminated.
In file included from decl.c:1:0:
/usr/include/stdio.h:27:10: fatal error: bits/libc-header-start.h: No such file or directory

include <bits/libc-header-start.h>

      ^~~~~~~~~~~~~~~~~~~~~~~~~~

compilation terminated.
In file included from /usr/lib/gcc/x86_64-linux-gnu/7/include-fixed/limits.h:194:0,
from /usr/lib/gcc/x86_64-linux-gnu/7/include-fixed/syslimits.h:7,
from /usr/lib/gcc/x86_64-linux-gnu/7/include-fixed/limits.h:34,
from tests.c:3:
/usr/include/limits.h:26:10: fatal error: bits/libc-header-start.h: No such file or directory

include <bits/libc-header-start.h>

      ^~~~~~~~~~~~~~~~~~~~~~~~~~

compilation terminated.
Makefile:11: recipe for target 'btest' failed
make: *** [btest] Error 1

解决方法

解决方法

Installed systemd unit for VNC Server in Virtual Mode daemon
Start or stop the service with:
systemctl (start|stop) vncserver-virtuald.service
Mark or unmark the service to be started at boot time with:
systemctl (enable|disable) vncserver-virtuald.service

虚拟机配置vncServer

bitXor

仅使用&和~14步之内完成^

解决思路

通过列举异或(^)，按位与(&)和取反(~)在不同情况下的计算结果可以得到如下结果

^
1 1 0 0
1 0 1 0
0 1 1 0

&
1 1 0 0
1 0 1 0
1 1 1 0

~
1 0
0 1

为了描述的方便，设两数为x和y。通过上述表格不难发现，~(x & y)与(x^y)的结果仅仅在0 0这一种情况下是不正确的，考虑解决这一问题
0 0这种情况运算结果是1，正确结果应当为0，~(~x & ~y)得到的结果恰好可以仅将0 0这种情况结果为0，其他所有情况为1，再&，恰好可以在不变动其他情况的条件下修正0 0的结果

tmin

仅使用! ~ & ^ | + << >>，4步之内获取最小的32bit的二进制补码整数
w位补码所能表示的范围为\([-2^{w - 1}, 2^{w - 1} - 1]\)
即1 << 31

isTmax

仅使用 ! ~ & ^ | +，10步之内判断一个数据是否为最大的32bit的二进制补码整数

我的最初想法是

int isTmax(int x) {
  return !(~(x + 1) ^ x);
}

我想的是需要用一种方式区分开最大值和其他值
这样想的理由是只有在x为最大值时，通过~(x + 1)这种溢出的运算才可以获取到最大值，然后与x异或最大值时为0，再取反得到1
可能这种通过运算溢出的方式不可行
其实回过头来想，判断一个数是否为最大值，只需要用最大值和它异或即可
我的方式也是想办法获得最大值，可是最大值可以直接表示
我忽略了一点，题目不允许使用超过255的数据，所以无法直接使用0x7fffffff,
而且无法使用移位操作，因此无法构造出最大值
所以只能考虑假设x为最大值，如果操作x构造出最大值
其实上面的做法中通过~(x + 1)是正确得到0x7fffffff的方法
但是答案不正确，是因为-1的存在
换言之， x + 1 = ~x, x == 2147483647 or -1
把这个问题真正解决了可以发现，应该是这么想，恰好发现2147483647+1的结果与2147483647正好是取反的关系
因此把2147483647+1反过来再与2147483647异或恰好可以得到0，这里其实想的并不是去构造最大值2147483647
而我想的是去构造2147483647，所以没有关注到这里会出问题，我实际上找的是x + 1 = -x这样的x，没想到除了2147483647，-1也是解，
因此考虑如何区分2147483647和-1，当我看到-1+1的结果是全0后，考虑到这样一个问题
只有!0=1,其他所有数!结果均不为1，前半部分只有2147483647和-1=0，其他均为1，后半部分只有-1为1，其他均为0
而|会使除-1以外的数据运算结果不变2147483647还是0，其他还是1，而-1会从0变成1，从而就单独把2147483647区分出来了

这道题如果允许使用移位符其实和下面的allOddBits就是一样的了

allOddBits

原理：x ^ x = 0
检测是不是奇数位全为1，只需要构造出奇数位全为1即可，
首先&一下是为了获得奇数位全为1的形式，如果x不符合条件，那么&之后的奇数位一定有为0的，^之后的结果就不是0

negate

负数的补码表示恰好为正数二进制取反加一

isAsciiDigit

不处在0x30和0x39范围的条件为
1.前面不是3
2.后面大于9
我在做的时候不会的是如何判断后面是不是大于9，暴力想法是判断它是不是10，11，12，13，14，15
但是应当从二进制的角度去想是不是大于9，大于9只需要首位为1，后面两位任意一位为1
(x & 0xF0) ^ 0x30错误原因在于& 0XF0,当遇到一个位数大于8位的数字时，从第9位往高位的所有数字都会被0xF0填充的0变成0
因此只要低8位是0x30，前面不管是多少异或的结果都是0
其实0xF0的意图是想把低4位清0，以便比较低8位中的高4位，但是高位补的0使得结果出现错误
如果用我的想法，只要低8位处在合法范围内就会将这个数判断为合法的，原因就是高位的数据被0xF0补充的0所消灭了

conditional

需要根据x的是否为0获得y或z
通过运算可以得到如下结果

x !x !!x !!x - 1 ~(!!x - 1)
不是0 00000000000000000000000000000000 00000000000000000000000000000001 00000000000000000000000000000000 11111111111111111111111111111111
0 00000000000000000000000000000001 00000000000000000000000000000000 11111111111111111111111111111111 00000000000000000000000000000000

我的想法是首先把x转化成一个对应的逻辑值0或者1，也就是通过两次!运算

然后发现如果想取y那么只需要用全1和它进行&运算，同时用全0与z进行&运算，如果想取z则把这个运算返过来

所以目前的任务是把!!x的结果能够满足上述运算的效果，也就是要通过!!x获得一个全0和全1

但是通过上表可以发现，!!x有两种结果，而我们必须通过一个相同的操作获得全0或者全1，可以发现-1恰好可以满足，而该题不允许使用减号，因此通过加-1实现，而-1的二进制恰好为对0取反

在解决问题之后，我们回过头来看这个表格，可以发现，可以不经过!!这个过程，方法是利用数据左移是逻辑移位，右移是算数移动，所谓算数移位是指在向右移动时，左侧补充的值是符号位，如果想让全0还是全0，0000...001变成全1，只需要让!左移31位，再右移31位置，即可以相同的方式实现从!x到!!x-1的转换

isLessOrEqual

很容易想到判断x是否小于等于y，只需要判断x与y的差值是否是小于等于0的即可
x和y的符号有下面几种可能

x的符号 y的符号 x符号位 y符号位
+ + 0 0
+ - 0 1
- + 1 0
- - 1 1

上面通过减法的结果判断两数大小关系是正确的思路，但是在进行减法时，异号之间可能会发生溢出
而异号之间仅通过符号位就可以判断出大小关系了，不需要进行减法
通过上表可以发现可以区分同号和异号的是符号位异或的结果，同号符号位异或结果为0，异号符号位异或结果为1
而且可以发现，在异号时x是否小于等于y的结果与x的符号位恰好相同
通过上述得到的性质可以使在同号时使用减法来判断大小关系，在异号时通过符号位判断大小关系
符号位异或的结果就像是一个开关，在一种情况下打开一个，关闭另一个，另一种情况则正好相反

logicalNeg

这个问题没有想出来
最初的思路显然需要找到0和其他数据之间的区别，我认为这道题之所以没有想出来问题就出在这里
我的关注点始终放在了一个单独的数据上，从最终答案来看关注点应当是两个数据
我想的始终是对于一个非0的数据，怎么才可以将它与0区分开来，但是始终找不到可行的方法
如果把数据按照数轴列的方式列出来，或许我可以发现相反数的存在
0和-2147483647的相反数是它们本身，其他数的相反数符号位一定与原数符号位相反
通过符号位来进行区分
同时1bit的0和1之间的相互转化，可以使用!也可以使用^运算

howManyBits

题目中给了几个Example，看前几个的时候还是很明确的，但是到了-1就糊涂了，
在补码中

  • 对于正数，默认值都是0，因此最高位的1代表着数据表示的结束
  • 对于负数，因为负数的补码是正数取反得到的，因此默认值为1，因此最高位的0代表着数据表示的结束
    因此对于正数，找到最高位1所在位数+1即为答案，对于负数，找到最高位0所在位数+1即为答案
    显然-1对应的答案也是满足上述方法的，只是确实不太好理解，因为它只留下了一个符号位，既是符号位同时转为原码后也能代表+1
    正数和负数的寻找目标是不同的，但是可以对负数按位取反，从而将正负数的操作统一为寻找最高位的1
    到此为止，还是通过思考可以想出来的，后续的问题就是如何得到最高位1所在的位数
    单就统计位数这个问题我就没有相出什么办法，没想出来怎么可以实现计数
    方法是看看高16位是否存在1，如果存在，那么位数计数要从16开始(这个可以通过移位实现)
    之后把原来的数据变成原来的高16位或低16位，这取决于高16位是否存在1
    之后看高8位，按照相同的过程直到变成看高1位从而找到1
    判断一个数中有没有1等价于看这个数是否为0，通过!运算即可实现
    !!(x >> 16):x的高16位是否存在1
  • 存在1，那么接下来的寻找空间就由原来的32bit变为高16bit，因此需要把x右移16位，而答案位数最低也是16了，因此还要对答案累积16，因此可以发现x要移动的位数和答案要累积的数值是相等的，所以直接对!!(x >> 16)进行移位
  • 不存在1，寻找空间由原来的32bit变为低16bit，x需要右移0位，答案位数最低为0
    上述两种情况都按照存在1的方式进行移位均可以得到正确结果
    如果!!(x >> 16)为1代表最高位1存在于高16位，假设最高位1位于17bit，那么此时bit_16的结果代表最高位1的后面一位
    bit_1代表在2位中最高位1是否存在于高1位，把bit_16到bit_1的结果相加得到的应当是最高位1所在位置的下一位，比如最高位1处在4，那么bit_16到bit_1的和就是3，处在4的下一位
    而我们的目标是最高位的1所处的位置，而非最高位1的下一位所处的位置
    因此还需要加上最高位1本身，但是这里不能直接+1，如果存在最高位1，直接加1确实可以，但是如果不存在最高1应当加0
    所以一个等效的办法是加上最后处理完成后的仅剩1位的x，x如果是1代表存在最高位1，那么加1，即加上它本身的位置，x如果为，说明不存在最高位1，加上0答案也是正确的

float_twice

  1. exp不为全0或全1，全0和全1有特殊用途

  2. 阶码E=exp-bias(偏置值)，exp是无符号数据的值，bias有计算公式\(2^{k - 1} - 1\)，在单精度浮点数中=127

  3. 尾数M存在规格化的问题，表示为1.xxx的形式，把原数中的小数点左移，通过阶码来表示这种移动

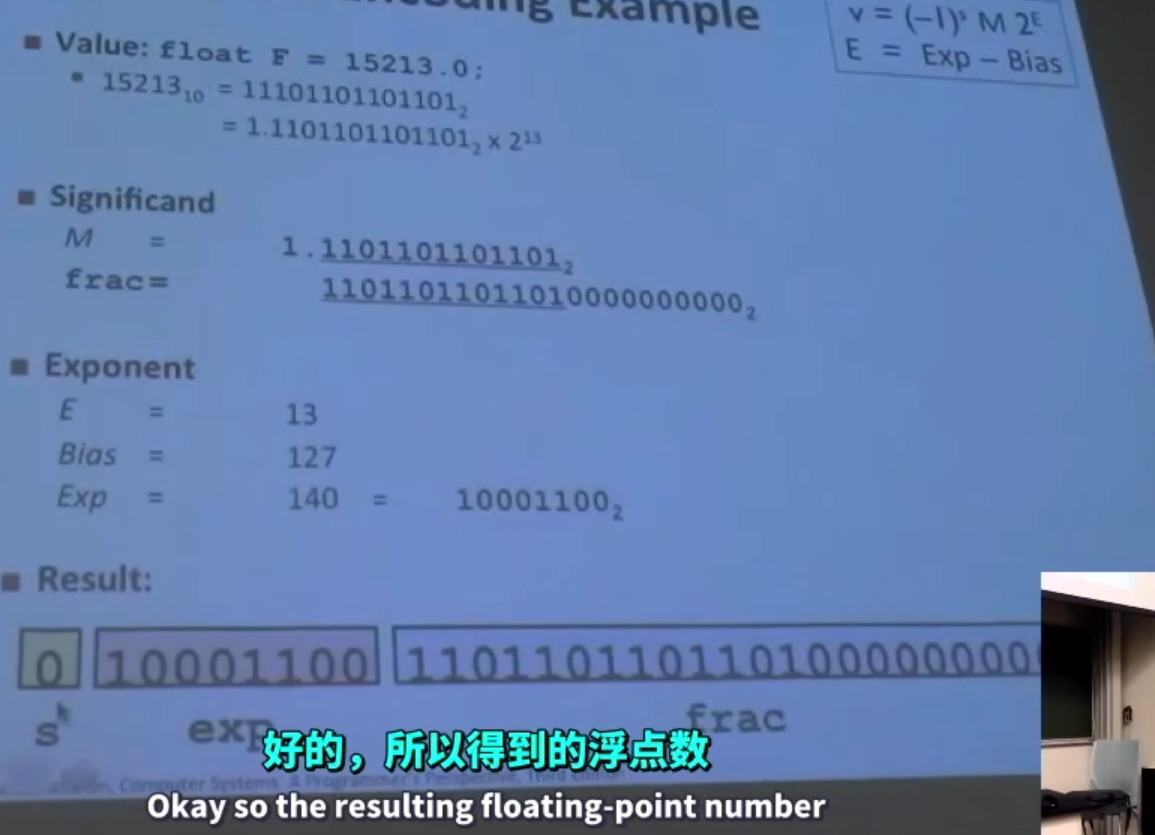
frac之所以向右侧补0，是因为frac表示的是小数点右侧的数值，是从左侧开始计数的，因此向右侧补0，就像小数点左侧是从右侧开始计数，向左侧补0

单精度格式分类

以下公式的立足点在于已知上图中的数据推导出原数，即从exp和f推导出E和M

  1. 规格化

    \(E = exp - Bias(exp = E + Bias)\)

    \(M = 1 + f(M = 1.f_{n - 1}f_{n - 2}...f_{0})\)，所以f实际是将M小数点移到左侧最高位之后的位置，小数点右侧的内容

  2. 非规格化

    非规格化数的用途是：1.表示0； 2.表示非常接近0的数

    阶码域为全0时，即\(exp=0\)时

    如果按照规格化的规定，应当有\(E = 0 - Bias = -Bias\)，但是却规定\(E = 1 - Bias\)

    M = f, 即f表示的小数是多少M就是多少，与规格化的区别在于缺少了隐含的开头的1

  3. 无穷大

    exp为全1，frac为全0，s为0时代表正无穷，s为1时代表负无穷

  4. NaN

    exp为全1，frac不为0时，表示不能是实数和无穷的数值

解题

对于给定的一个数据，存在以下几种情况

  1. 规格化数

    exp+1即可，但要考虑是否会发生溢出

    如果结果变为全1，是不是要返回无穷，没道理变成Nan，变成无穷是不是还要把frac变成全0。答案是对的，规格化数的最大值的exp加1后应当变为无穷，确实要把frac修改为全0

exp为全0

  1. 非规格化数

    感觉上是对frac直接乘2，如果超过非规格化范围怎么办？

    *2就是对frac直接左移1位，如果超过了非规格化的范围，最左侧的1会移动到exp的范围内，很神奇的是此时不需要进行任何操作结果恰好是正确的，这里可能和非规格化标准的定义有关系

exp为全1

  1. 无穷大和无穷小

    直接返回原数即可

  2. NaN

    直接返回Nan即可

需要注意的是这里没有仅能使用8bit数据的限制了，可以使用32bit的数据了，所以提取数据就变得简单许多

问题是把unsigned uf的uf的二进制直接当作浮点数了，不是说给定一个值要先转化为二进制然后再根据E和exp，f和M的关系转换为浮点数，而是它的二进制本身就是浮点数，这点我一直理解的有问题。因为题目中采用的是无符号数，而且把这个无符号数就当作了浮点数，所以在给定一个数据时它的二进制表现形式就直接被当作浮点数了，所以这也就是为什么2147483647是NaN了，因为它的二进制表现形式是0x7fffffff，对应exp位置的是0xff，对应frac位置的又不为0，刚好是浮点数中NaN的表现形式

float_i2f

作为参数的int可能是一个负数，但是在修改为float形式时，都是观察正数的情况的，之后修改符号位为1

把int转化为float，采用unsigned形式存储并返回

浮点数包含以下几种情况：

  1. 规格化

  2. 非规格化

  3. 无穷

  4. NaN

int的表示范围为[-2147483648， 2147483647]

这个范围内的数转化为float时，不会出现2(0除外)，3，4的情况

所以要处理的只是0和规格化数

由于不存在NaN和无穷的情况，所以exp还是很好处理的

难点在于frac的处理，一方面要考虑尾数不够23bit和超过23bit两种情况

不够23bit向左移，右侧自动补0不会出什么问题

如果超过23bit需要向右移，这时候出现一个问题是右侧被丢弃的位涉及到数据的舍入，IEEE默认的舍入的规则为向偶数舍入，通俗地说可以为4舍6入5取偶数，不够一半就舍弃，例如1.4->1，超过1半就升上去，例如1.6->2，刚好一半就向最接近的偶数靠近，例如1.5->2，2.5->2，对于3.5这种减少和增加都可以到达偶数的，默认升上去变为4

上面是以10进制为例的，2进制的规则见下方例子

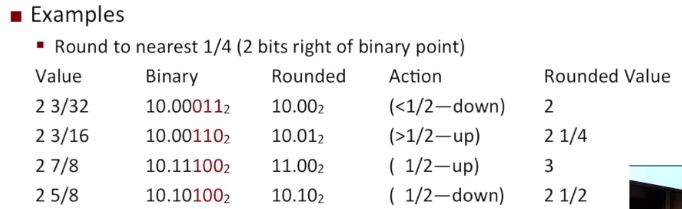
相当于保留精度到整数

  • xxx.0xxxx: 直接舍弃小数部分，不需要进行操作

  • xxx.10000 (对应else flag = frac & 1)

    • xx1.100000: 升上去 (flag = 1)
    • xx0.100000: 已经是偶数不需要处理的 (flag = 0)

  • xxx.10001: 升上去 (对应if (m & 1) flag = 1)

float_f2i

int转float时，由于int本身的限制，转float时并不会出现非规格化，无穷和NaN的数据

但是float转int时，由于float本身那几种形式都有可能出现，所以分开讨论

  1. 规格化

    exp不为全0和全1

  2. 非规格化

    exp为全0，结果是0(此处其实还有疑惑，为何浮点数向整形转换会直接舍弃掉小数部分？例如浮点数0.9转换为int时直接变为0)

  3. 无穷

    exp为全1，frac为全0，返回题目规定值

  4. NaN

    exp为全1，frac不为全0，返回题目规定值

容易被忽视的一点是，在规格化时，当exp计算得出的e过大使得表示的数据超出int的范围时应当返回题目规定值，所以这也就涉及到了如何判断是否溢出

int的最大值是01111111111111111111111111111111，即\(1.1...1 * 2^{30}\),所以我觉得当超过30时即会超出范围(此处还有疑问，超过30即\(>= 31\),但实际测试设置为\(> 31\)结果依然正确，尝试将溢出的范围设置更大时依然可以得到正确结果，尝试查看测试数据，但是没有找到)，巧合的是当浮点数为无穷和NaN时的e也是超出这个范围的，所以可以将操作进行合并

首先计算e，根据e即可区分几种情况

posted @ 2023-03-23 16:40  0x7F  阅读(130)  评论(0)  编辑  收藏  举报