状态机模型
状态机描述的是状态，以前的dp是只有1个或不多个状态，现在是把状态拆分为一个过程，把一个过程用确定的状态和状态之间的关系描述出来
常规方法考虑的是状态以及在不同状态下的计算方式，状态机考虑的是一个过程以及在这个过程中发生的状态变化
在大盗阿福一题中，
常规方法是考虑2种情况，一种是未选择当前房间，另一种是选择了当前房间，不同的选择对应着不同的更新方式，在本题中这种更新方式是易求的，想起来并不会很乱，但是在某些题目中这个过程可能很难划分
考虑的是从1个房间走向下一个房间的这个过程，状态机考虑的是这个过程所发生的状态的所有可能变化
01背包中每个物品选或不选都是独立的， 不受前者约束不对后者产生影响
状态机不一样，由于某些条件下的边不存在，于是我们在计算本次状态之前就可能需要了解前一次的状态，于是需要状态细分标记
当然上面所说的是传统问题中的01背包，大盗阿福一题采用背包的设计方式也是可以解决的，但是就不再是传统意义上的背包了，是需要考虑状态之间的关系的
只是在大盗阿福一题中这种关系并不是很多很复杂，可以直接分析出，若状态关系过于复杂，就无法采用背包划分集合的方式简单计算了，只能从状态机的角度考虑以降低思维难度
待考证理解：
背包->状态机
背包->状态压缩
状态机和状态压缩似乎是并列的两个点，背包作为传统的处理状态的方法，状态机和状态压缩则是采用其他方式来处理状态
大盗阿福
按照类背包的方法来做大盗阿福一题的转移方程和计算，所谓类背包，是由于在背包问题中，当前物品的选与不选，与之前物品是没有关系的，
但是在大盗阿福一题中，显然当前的选与不选是需要考虑之前的选与不选，抽象到模型上来说，状态与状态之间是否存在影响
若不存在影响，则可以考虑传统背包模型
若存在影响，当这种关系相对简单时，仍然可以采用背包的思考方式，但当关系复杂时，采用状态机，从过程入手，考虑状态的变化是更清晰的方法
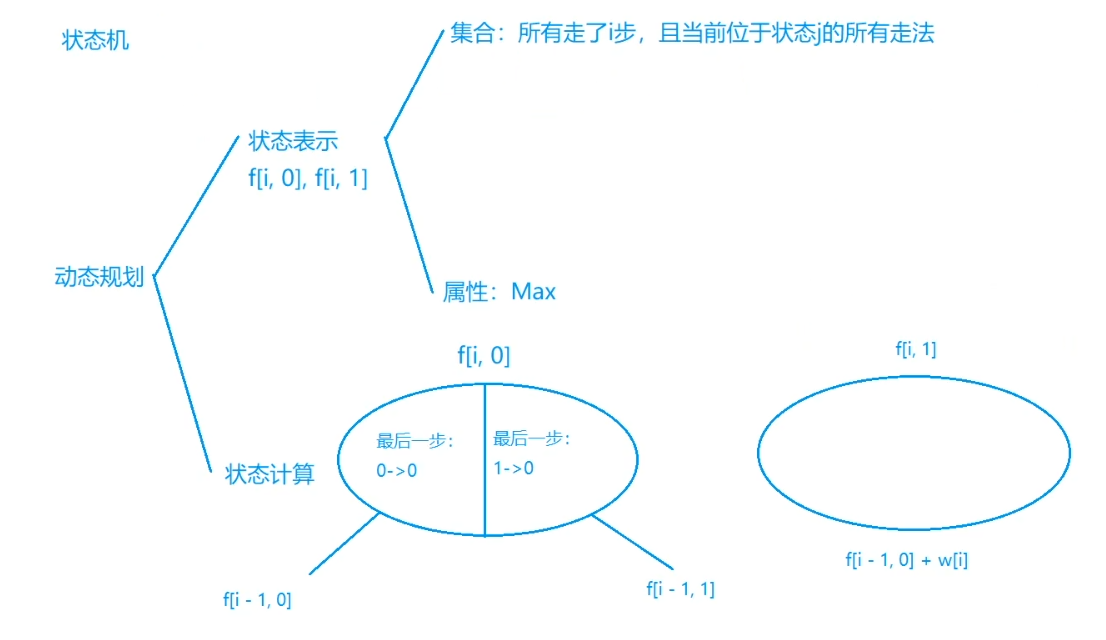
股票买卖4
从股票买卖一题中可以看出，一般的思路是从动作入手的，考虑这次要怎么做，当动作较多时是比较困难进行表达的，而采用状态表示可以简化模型，状态间的转变能够表示一定的动作
大盗阿福一题并没有很明显的体现出这一点，这是因为大盗阿福虽然采用了状态机，但是状态表示和采取的动作是相同的，并没有很明显体现出状态机的精妙之处
但股票买卖就体现出了，从动作角度的考虑和从状态角度的考虑见打卡的代码上方的注释
- 总交易次数的限制：状态表示方程中添加一个维度
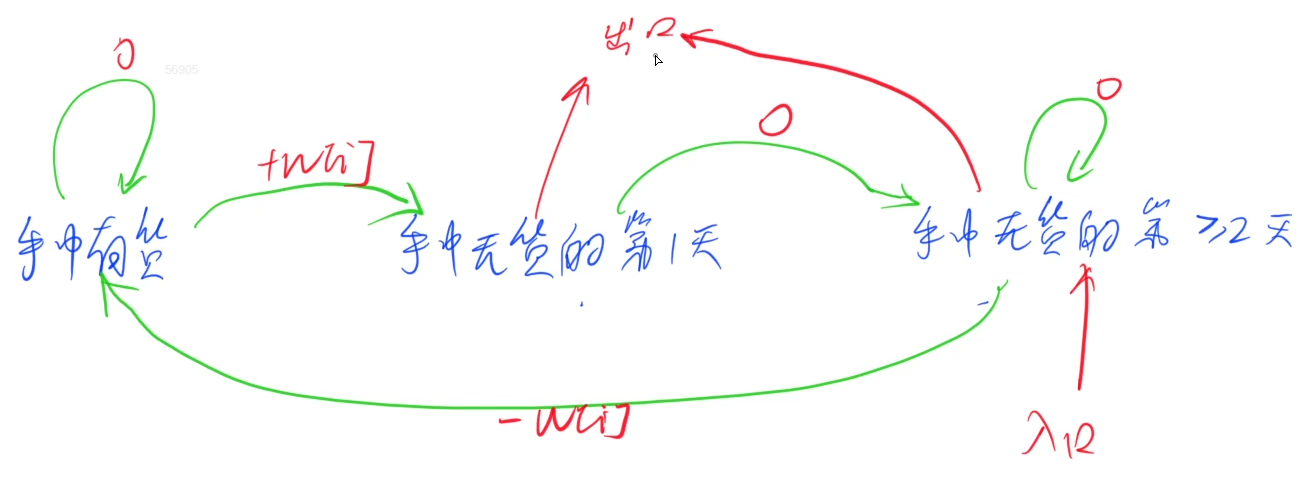
股票买卖5
