欧拉路径和欧拉回路
概念
- 欧拉路径：图&G&中的一条路径若包括每个边恰好一次，则其为欧拉路径
- 欧拉回路：一条回路如果是欧拉路径，那么其为欧拉回路
存在条件
无论无向图还是有向图，首要条件为所有边都是连通的
- 无向图
- 存在欧拉路径的充要条件：度数为奇数的点只能有0或2个
- 存在欧拉回路的充要条件：度数为奇数的点只能有0个
- 有向图
- 存在欧拉路径的充要条件：所有点出度=入度；或除两点外其余所有点出度=入度，余下两点一个出度-入度=1(地点)，另一个入度-出度=1(终点)
- 存在欧拉回路的充要条件：所有点出度=入度
注：欧拉回路为欧拉路径的一种特例，因此如果说存在欧拉路径是包含存在欧拉回路这种情况的
算法流程
1. 建图并统计点的度数(有向图分入度和出度)
2. 根据度数进行初步的有解性判定
如何理解"初步"：所有点的度数均满足要求不等价于所有边均连通。连通性判定在此处无法解决，因此为初步的合法性判定
-
无向图
统计度数为奇数的点个数count- 欧拉回路：
count == 0 - 欧拉路径：
count == 0 || count == 2
- 欧拉回路：
-
有向图
- 欧拉回路：有解仅需保证所有点入度==出度即可
- 欧拉路径：
设din[i]为i点的入度，dout[i]为i点的出度
dout[i] - din[i] == 1的点数为startNum(满足起点特征)
din[i] - dout[i] == 1的点数为endNum(满足终点特征)
success表示是否有解
方法1:
for (int i = 1; i <= n; ++i) // 枚举所有点 if (din[i] != dout[i]) { if (dout[i] - din[i] == 1) ++ startNum; else if (din[i] - dout[i] == 1) ++endNum; else success = false; }有解的条件为
success && (!startNum && !endNum || startNum == 1 && endNum == 1)
比较容易理解的是success为false时一定是无解的
不容易理解的是，success为true时不一定是有解的，因为最多只能有2个点的出度!=入度，而success为true并不能保证这一点方法2:
设count为出度!=入度的点个数，flag为出度!=入度点的(出度-入度)的乘积(或者入度-出度的乘积)for (int i = 1; i <= n; ++i) // 枚举所有点 if (din[i] != dout[i]) { ++count; flag *= dout[i] - din[i]; }有解的条件为
!count || (count == 2 && flag == -1)
即出度!=入度的点数为0 或 出度 != 入度的点数为2并且对应两个点，起点满足dout[i] - din[i] == 1, 终点满足dout[i] - din[i] == -1
注：如果题目保证至少存在一组解，则此判定过程可以省略
3. 选取起点
首先需要明确两点
- 从欧拉回路上任意一点
dfs均可搜索到其所在的欧拉回路- 从欧拉路径上任意一点
dfs未必可以搜索到其所有的欧拉路径，必须从满足一定性质的点出发才可
原因很简单，对于一个环路来说，从任意一点开始都可以一笔画出整个环；对于一个路径，只有从起点开始才可以一笔画出整条路径
- 欧拉回路：如果题目要求的为欧拉回路，在无向图中，满足所有点的度数为偶数，在有向图中，满足所有点的出度==入度，所有点都是等价的，因此
dfs的起点只需定为一个非孤立点
为何一定是非孤立点: 在此类题目中，一般不能保证点是连通的，因此是存在孤立点的，但是孤立点的存在对欧拉回路或路径的存在并不产生影响，但是如果从孤立点开始是找不到回路或路径的
- 欧拉路径：如果题目要求的为欧拉路径，对于无向图，需要找到度数为奇数的点作为起点，对于有向图，需要找到
dout[i] - din[i] == 1的点\(i\)
4.从起点开始dfs寻找欧拉回路或欧拉路径
欧拉回路和欧拉路径问题的本质是边的问题，类比对点的dfs问题，我们同样需要对走过的边进行标记，防止重复
void dfs(int u)
{
for (int i = h[u]; ~i; i = ne[i])
{
if (st[i]) continue; // 对走过的边进行标记
st[i] = true;
dfs(e[i]);
res[++cnt] = i;
}
}
dfs部分难点-递归搜索和存储答案的顺序问题
dfs(e[i]);
res[++cnt] = i;
在常规dfs中，搜索到某个点会首先把该点进行存储，然后再递归搜索，但是求解欧拉路径需要递归搜索完一个节点后再把到该节点的边进行存储
为了说明这两种顺序产生的不同结果，以一组数据为例
/**
* 无向图
* 5个点，6条边
* 以下6行a b表示：a与b之间有一条边
*/
5 6
2 3
2 5
3 4
1 2
4 2
5 1
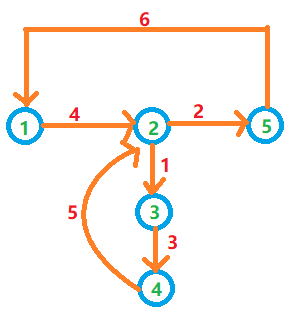
对边进行存储，
- 如果采取先存储再搜索的顺序，结果为
4 2 6 1 3 5 - 如果采取先搜索再存储的顺序，结果为
6 2 5 3 1 4
可以发现，第二种顺序得到的恰好是欧拉路径的倒序，结果只需要倒序输出即可
dfs部分难点-优化问题
最终的优化方案实际分为两个部分，为了更加透彻理解优化原理，逐层进行分析
- 原始思路
void dfs(int u)
{
for (int i = h[u]; ~i; i = ne[i])
{
if (st[i]) continue; // 对走过的边进行标记
st[i] = true;
// 如果为无向图，这里还需要对反向边进行标记
dfs(e[i]);
res[++cnt] = i;
}
}
上述代码为一般思路，存在的问题为走过的边存在重复枚举。添加了st[]用于对边进行判重，只能保证不去走已经走过的边，但是不能保证不去枚举已经走过的边。
考虑下面的情况，对于\(1\)号点，第一步走到\(2\)号点，则\(1->2\)的边被搜索过了，但从\(2->5->1\)又一次走到\(1\)号点时，for循环还会枚举一次\(1->2\)这条边，st的存在使得不会去走这条边，但是仍会枚举这条边
只要这条边没有被删除，那么只要到达\(1\)号点，\(1->2\)这条边就会被枚举一次，显然这是一次无效的枚举，当无效枚举次数过多时就会TLE
/**
* 无向图
* 5个点，6条边
* 以下6行a b表示：a与b之间有一条边
*/
5 6
2 3
2 5
3 4
1 2
4 2
5 1
- 第一次优化
上述分析提到，“只要一条已经走过的边没有被删除，那么就有可能发生无效枚举”，因此优化方案为删除已经走过的边
在链式结构中，如果不采用双向链表无法在\(O(1)\)的时间内删除某点，而以现有的存储结构是无法做到这一点的同时改变存储结构相对复杂，因此采取如下方案
对于队首指针(h[u])指向的第一条边\(i\)
- 如果其已经被搜索过(
st[i] == true)，那么直接删除，因为是第一条边，因此可以通过直接修改队首指针(h[u] = ne[i])实现，然后继续枚举下一条边 - 如果其没有被搜索过(
st[i] == false)，那么删除这条边，并标记该边走过，然后对该边的后续节点进行枚举
for (int i = h[u]; ~i; i = ne[i])
{
if (st[i])
{
h[u] = ne[i];
continue;
}
h[u] = ne[i];
s[i] = true;
// 无向图还需要对反向边进行标记
dfs(e[i]);
res[++cnt] = i;
}
注：第2种方案中，既然已经将边删除，为何还需要进行标记？
答：这里不标记也是对的，因为该边起点的队首指针已经被修改，因此不会再搜索到这条边，因此不标记对答案也不会产生影响。
但是在无向图中，我们能删除的仅是当前这个方向，而不能修改反方向。我们虽然可以获取到反方向边的编号，但是通过修改h数组来实现删边的前提是当前边为队首指针指向的第一条边，而我们无法保证当前边的终点的队首指针指向的是当前边的反向边，因此无向图中方向边必须进行标记而非删除，既然有些边实际被走过只进行了标记但却没有删除，因此if(st[i])的判断也是不可以省略的
按照注中分析，将边删除后可以不进行标记，即下方代码，但显然这样做并没有大幅度减少代码量反倒增加了思维量，因此一般情况下会选择既标记又删除
for (int i = h[u]; ~i; i = ne[i])
{
if (st[i])
{
h[u] = ne[i];
continue;
}
h[u] = ne[i];
// 无向图还需要对反向边进行标记
dfs(e[i]);
res[++cnt] = i;
}
- 第2次优化
第1次优化后的代码仍然存在的问题是，我们仅仅通过修改h[]实现了删边，但是ne[]的信息并没有同步发生变化。
由于代码采取的递归加回溯的实现方式，因此可能发生的情况是递归过程中一些边被删除了，但当回溯时，由于ne[]的信息没有改变，所有仍有可能搜索到这些边，这些无效搜索仍可能造成TLE
一个典型的例子为，图中仅一个点，很多条自环，考虑第一层dfs所有第一条边，其下的所有层递归会将所有边删除，但是回到第一层时i = ne[i]会继续搜索它的下一条边
解决方法为让每次的i都从队首指针指向的第一条边开始搜索(h[u])，因为我们的搜索策略保证了h[u]始终为第一条未搜索过的边，因此可以从h[u]开始从而消除因ne[]与h[]信息不同步带来的影响
for (int i = h[u]; ~i; i = h[u])
{
if (st[i])
{
h[u] = ne[i];
continue;
}
h[u] = ne[i];
st[i] = true;
// 无向图还需要对反向边进行标记
dfs(e[i]);
res[++cnt] = i;
}
5. 根据dfs结果进行终极判定
dfs后得到一个答案序列，此时需要判断序列中边的条数与总边数的关系，因为分析到这里我们仍然没有确定所有边是否均连通，因此获得的序列并不一定是合法的
只有在各点满足了度数的要求，并且判定出所有边均连通的条件下，才可以判定出欧拉回路或欧拉路径是存在的
- 如果答案序列中边的数目等于总边数，说明所有边是连通的，且成功找到了欧拉回路或欧拉路径
- 如果答案序列中边的数目小于总边数，说明不满足所有边连通的条件，即不存在欧拉回路或路径
例题
虽然在算法流程的讨论中，对欧拉回路和欧拉路径分开进行了讨论，但是由于欧拉回路是欧拉路径的一种特例，因此用欧拉路径的更具普适性的代码是可以解决欧拉回路的问题的，
只不过如果题目明确告知了是求欧拉回路，那么起点的的选取过程可以更简单，代码量更少一些
无向图求欧拉路径
题目描述
解题思路
本题核心为无向图求欧拉路径，但题目有两点特殊之处：
- 题目保证至少一个解。这保证了我们不需要根据度数进行初步的有解性判定，而且在选定起点
dfs之后也不需要比较答案序列中的边数和总边数的关系进行最终有解性判定 - 题目要求输出字典序最小的答案序列，只需保证优先搜索序号较小的点即可实现这一点，若采用邻接表存储在建图后还需要进行排序，同时会牵扯出很多问题，而采用邻接矩阵则可以不需要额外操作轻松实现这一点要求
代码实现
#include <iostream>
using namespace std;
const int N = 510, M = 1100;
int n, m;
int g[N][N];
int res[M], cnt;
int d[N];
void dfs(int u)
{
for (int i = 1; i <= n; ++i)
if (g[u][i]) {
--g[u][i], --g[i][u];
dfs(i);
}
res[++cnt] = u;
}
int main()
{
cin >> m;
for (int i = 0; i < m; ++i) {
int x, y;
cin >> x >> y;
++g[x][y], ++g[y][x];
++d[x], ++d[y];
n = max(n, max(x, y));
}
/**
* 这里不采用尝试性dfs的原因是，每次dfs都会对g数组进行修改，如果本次dfs没有得出结果还需要恢复原样，较为复杂，因此还是通过欧拉路径的性质找到合法的起点开始dfs
* 所谓尝试性dfs是指，不管通过本次dfs的点能够找到欧拉路径，都选择从这一点开始dfs试一试，如果不能那么再尝试dfs其它点
*/
// for (int i = 1; i <= n; ++i)
// if (!d[i]) {
// dfs(i);
// if (cnt == m + 1) break;
// cnt = 0;
// // 后续需要恢复dfs前的原样，恢复二维数组的过程比较浪费时间
// }
/**
* 为什么可以提前确定起点
* 首先合法的起点一定是非孤立点，即度数不能为0，可以保证孤立点一定不是起点
* 其次，如果存在度数为奇数的点，如果该点不作为起点，那么一定无法找到欧拉路径，所以只能将该点作为起点
*/
int start = 1;
while (!d[start]) ++start;
for (int i = 1; i <= n; ++i)
if (d[i] % 2) {
start = i;
break;
}
dfs(start);
for (int i = cnt; i; --i) cout << res[i] << endl;
return 0;
}
有向图求欧拉路径
题目描述
解题思路
本题的建图方式其实算是第一个难点，如果选取单词为点，两个单词是否存在可连接的关系为边，那么题目实际为一哈密顿路径问题
如果选取单词的首尾字母为点，每个单词为边，那么题目就会转化为有向图的欧拉路径问题
完成问题的转化之后，按照上述4个步骤进行求解即可
代码实现
有向图求欧拉路径在由度数初步判定合法性时，提出了两种方法，这里分别实现一下
// 方法1
#include <iostream>
#include <cstring>
using namespace std;
const int N = 30, M = 1e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int din[N], dout[N];
bool st[M];
int res[M], cnt;
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
for (int i = h[u]; ~i; i = h[u])
{
if (st[i])
{
h[u] = ne[i];
continue;
}
h[u] = ne[i];
st[i] = true;
dfs(e[i]);
res[++cnt] = i;
}
}
int main()
{
int T;
cin >> T;
while (T --)
{
cin >> m;
n = 0;
idx = cnt = 0;
memset(din, 0, sizeof din);
memset(dout, 0, sizeof dout);
memset(st, 0, sizeof st);
memset(h, -1, sizeof h);
for (int i = 0; i < m; ++i)
{
string str;
cin >> str;
int a = str[0] - 'a', b = str[str.size() - 1] - 'a';
add(a, b);
++dout[a], ++din[b];
n = max(n, max(a, b));
}
bool success = true;
int count = 0, flag = 1, start = 0, startNum = 0, endNum = 0;
while (!din[start] && !dout[start]) ++start;
for (int i = 0; i <= n; ++i)
if (din[i] != dout[i])
{
if (dout[i] - din[i] == 1)
{
start = i;
++startNum;
}
else if (din[i] - dout[i] == 1) ++endNum;
else
{
success = false;
break;
}
}
if (success && (!startNum && !endNum || startNum == 1 && endNum == 1))
{
dfs(start);
if (cnt == m) cout << "Ordering is possible." << endl;
else cout << "The door cannot be opened." << endl;
}
else cout << "The door cannot be opened." << endl;
}
return 0;
}
// 方法2
#include <iostream>
#include <cstring>
using namespace std;
const int N = 30, M = 1e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int din[N], dout[N];
bool st[M];
int res[M], cnt;
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
for (int i = h[u]; ~i; i = h[u])
{
if (st[i])
{
h[u] = ne[i];
continue;
}
h[u] = ne[i];
st[i] = true;
dfs(e[i]);
res[++cnt] = i;
}
}
int main()
{
int T;
cin >> T;
while (T --)
{
cin >> m;
idx = cnt = 0;
memset(din, 0, sizeof din);
memset(dout, 0, sizeof dout);
memset(st, 0, sizeof st);
memset(h, -1, sizeof h);
for (int i = 0; i < m; ++i)
{
string str;
cin >> str;
int a = str[0] - 'a', b = str[str.size() - 1] - 'a';
add(a, b);
++dout[a], ++din[b];
n = max(n, max(a, b));
}
int count = 0, flag = 1, start = 0;
while (!din[start] && !dout[start]) ++start;
for (int i = 0; i <= n; ++i)
if (din[i] != dout[i])
{
++count;
flag *= dout[i] - din[i];
if (dout[i] - din[i] == 1) start = i;
}
if (!count || (count == 2 && flag == -1))
{
dfs(start);
if (cnt == m) cout << "Ordering is possible." << endl;
else cout << "The door cannot be opened." << endl;
}
else
cout << "The door cannot be opened." << endl;
}
return 0;
}
