01分数规划问题
数学描述
给定\(n\)个二元组\((value_i,\ cost_i)\)。\(value_i\)是选择此二元组获得的价值（非负）, \(cost_i\)是选择此二元组付出的代价（非负），设\(x _i\) \(( x_i ∈ \{ 0 , 1 \} )\)代表第\(i\)个二元组的选与不选，最大(小)化下式
\(maximize(or minimize) \ r = \frac{\sum{(value_i*x_i)}}{\sum{(cost_i * x_i)}}\)
问题引入
为了便于理解该问题解法的推导过程，通过以下问题的解决过程引出基本01分数规划问题的解法
问题描述
给定一张\(L\)个点、\(P\)条边的有向图，每个点都有一个权值\(f[i]\)，每条边都有一个权值\(t[i]\)。
求图中的一个环，使“环上各点的权值之和”除以“环上各边的权值之和”最大。
输出这个最大值。
[注]: 数据保证至少存在一个环
输入格式
第一行包含两个整数\(L\) 和 \(P\)。
接下来\(L\)行每行一个整数，表示\(f[i]\)。
再接下来 \(P\) 行，每行三个整数 \(a，b，t[i]\)，表示点 \(a\) 和 \(b\) 之间存在一条边，边的权值为 \(t[i]\)。
输出格式
输出一个数表示结果，保留两位小数。
数据范围
\(2≤L≤1000\),
\(2≤P≤5000\),
\(1≤f[i],t[i]≤1000\)
输入样例
5 7
30
10
10
5
10
1 2 3
2 3 2
3 4 5
3 5 2
4 5 5
5 1 3
5 2 2
输出样例
6.00
解决思路
此题型的解决方法为二分+spfa判负环
本题是求最值的问题，所以二分不难想到，然后还需要判断是否可以采用二分
- 使用二分的首要条件是二分对象的取值是可知的
- 条件1满足，答案区间为\((0, 1000]\)
- 满足条件1之后，给定一个mid，假设具有某种方法来判定一个该值是否符合条件，考虑在得知此值合法性的前提下，是否可以将原取值范围缩减
- 条件2满足，给定一个mid值，假设\(\frac{\sum{f[i]}}{\sum{t[i]}} > mid\)，那么答案处在mid的右半区间，反之处在左半区间
- 如果满足了条件2，那么考虑是否具有某种方法来判定mid的合法性，如果不能判断那么前面的假设就不成立，二分法不可取，反之可取
- 需要判断\(\frac{\sum{f[i]}}{\sum{t[i]}}\)与\(mid\)的大小关系，那么就假设\(\frac{\sum{f[i]}}{\sum{t[i]}} > mid\)，推导后可得\(mid * \sum{t[i]} - \sum{f[i]} < 0\)。即对于一个边权为\(mid*t-f\)的图，判断是否存在一个负环(注意后面这里是t和f，代表一个点权和边权，而非点权和，边权和)来判断mid的合法性，条件3成立
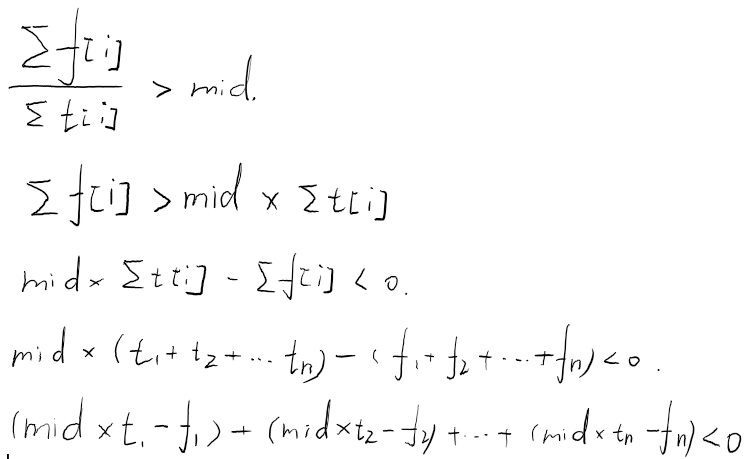
代码实现
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1010, M = 5010;
int n, m;
int f[N];
bool st[N];
int cnt[N];
double dis[N];
int h[N], e[M], ne[M], w[M], idx;
void add(int a, int b, int t)
{
w[idx] = t;
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++;
}
// 有负环返回true，否则返回false
bool spfa(double x)
{
queue<int> q;
for (int i = 1; i <= n; ++ i)
{
cnt[i] = 0;
dis[i] = 0.0;
q.push(i);
st[i] = true;
}
while (q.size())
{
int t = q.front(); q.pop();
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int p = e[i];
if (dis[p] > dis[t] + x * w[i] - f[t])
{
dis[p] = dis[t] + x * w[i] - f[t];
cnt[p] = cnt[t] + 1;
if (cnt[p] >= n) return true;
if (!st[p])
{
q.push(p);
st[p] = true;
}
}
}
}
return false;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++ i)
cin >> f[i];
memset(h, -1, sizeof h);
for (int i = 0; i < m; ++ i)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
double l = 0.0, r = 1000.0;
const double eps = 1e-6;
while (r - l > eps)
{
double mid = (l + r) / 2.0;
if (spfa(mid)) l = mid;
else r = mid; // 浮点数不需要加减1
}
printf("%.2lf\n", l);
return 0;
}
