BFS总结

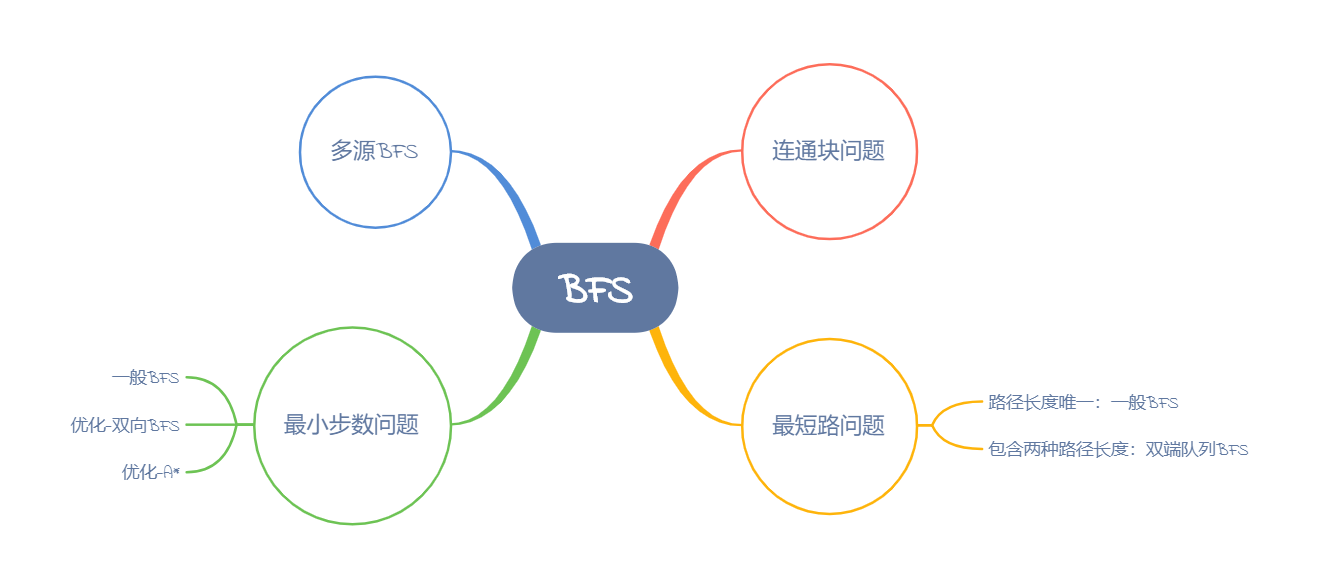
说明

为了突出各类题目的区别，以下例题均选择较为简单的题目。不会涉及一些非常巧妙的技巧，摆脱一些细枝末节，以便更多地关注到题目类型本身

连通块问题

题目描述

农夫约翰有一片 \(N∗M\) 的矩形土地。

最近，由于降雨的原因，部分土地被水淹没了。

现在用一个字符矩阵来表示他的土地。

每个单元格内，如果包含雨水，则用”W”表示，如果不含雨水，则用”.”表示。

现在，约翰想知道他的土地中形成了多少片池塘。

每组相连的积水单元格集合可以看作是一片池塘。

每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。

请你输出共有多少片池塘，即矩阵中共有多少片相连的”W”块。

解题思路

遍历所有格子，如果为"W"并且未曾标记过，则从此格子开始搜索，标记其周边所有可达的"W"并进行计数

解题代码(C++)

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>

using namespace std;

typedef pair<int, int> PII;

const int N = 1010, M = N * N;

int n, m;
char g[N][N];
bool st[N][N];
PII q[M];
int dx[] = {-1, -1, -1, 0, 0, 1, 1, 1};
int dy[] = {-1, 0, 1, -1, 1, -1, 0, 1};

void dfs(int sx, int sy)
{
    int hh = 0, tt = -1;
    q[++ tt] = {sx, sy};
    st[sx][sy] = true;

    while (tt >= hh)
    {
        PII t = q[hh ++];
        int xx = t.first, yy = t.second;

        for (int i = 0; i < 8; ++ i)
        {
            int x = xx + dx[i], y = yy + dy[i];
            if (x < 0 || x >= n || y < 0 || y >= m || g[x][y] == '.' || st[x][y]) continue;

            q[++ tt] = {x, y};
            st[x][y] = true;
        }
    }
}
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; ++ i) cin >> g[i];

    int res = 0;
    for (int i = 0; i < n; ++ i)
        for (int j = 0; j < m; ++ j)
            if (g[i][j] == 'W' && !st[i][j])
            {
                ++ res;
                dfs(i, j);
            }

    cout << res << endl;


    return 0;
}

最短路问题

BFS同最短路算法一样，都是用来解决图上最短路问题，不同的是BFS对图有一些更为严格的要求

最短路算法可以解决单源最短路和多源最短路，路径长度只存在是否存在负权边和负权回路的区分

但BFS只能解决单源最短路，并且路径长度只能是全部相等或只存在两种值(由此分为以下两类)

路径长度均相等

题目描述

给定一个 \(n × n\) 的二维数组，如下所示：

int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。

数据保证至少存在一条从左上角走到右下角的路径。

解题思路

采用队列，实现层序遍历。所有点只会入队一次，且出队时对应的路径即为最短路径

证明出队时得到的距离一定为最短距离:

• 方法1-借助Dijkstra算法

  1. 首先需要根据数学归纳法证明采用队列进行层序遍历的BFS具有两段性和单调性

     例如序列 \(|x, x, x, | x+1, x+1, x+1|\)，其具备两段性是指数据最多可以分为两部分，即这里的x和x+1

     首先选择队头元素x进行扩展，假设边的距离均为1，那么由它扩展出的距离均为x+1，放到队尾，显然序列仍然满足两端性和单调性

  2. 在满足两段性和单调性的前提下，考虑堆优化版Dijkstra算法。每次从优先队列的对头取出元素，并更新所有相邻的点，对于遍历顺序而言同样具有两段性和单调性，所以与我们目前的做法是一致的。由于Dijkstra算法是正确的，所以目前的做法就是正确的

• 方法2-直接证明

  ​ 利用反证法，假设此时队头元素\(s\)并非最短距离，即后续状态中存在\(t\)，满足\(dis[s] > dis[t] + w\)。在方法1中已经证得，序列满足单调性，即\(dis[s] <= dis[t]\)，与假设发生矛盾，所以假设不成立，即队头元素s一定为最短距离。

解题代码(C++)

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>

using namespace std;

typedef pair<int, int> PII;

const int N = 1010, M = N * N;

int n;
int m[N][N];
bool st[N][N];
int dx[] = {-1, 0, 1, 0};
int dy[] = {0, 1, 0, -1};

PII q[M];
PII path[N][N];
PII nextLoca[N][N];


void bfs(int sx, int sy)
{
    int hh = 0, tt = -1;
    q[++ tt] = {sx, sy};
    st[sx][sy] = true;

    while (tt >= hh)
    {
        PII t = q[hh ++];
        int xx = t.first, yy = t.second;
        for (int i = 0; i < 4; ++ i)
        {
            int x = xx + dx[i], y = yy + dy[i];
            if (x < 0 || x >= n || y < 0 || y >= n || st[x][y] || m[x][y]) continue;

            st[x][y] = true;
            q[++ tt] = {x, y};
            nextLoca[x][y] = {xx, yy};
        }
    }
}
int main()
{
    cin >> n;
    for (int i = 0; i < n; ++ i)
        for (int j = 0;j < n; ++ j)
            cin >> m[i][j];

    nextLoca[n - 1][n - 1] = {n - 1, n - 1};
    bfs(n - 1, n - 1);

    PII t = {0, 0};
    while (1)
    {
        int x = t.first, y = t.second;
        cout << x << ' ' << y << endl;
        if (x == n - 1 && y == n - 1) break;
        t = nextLoca[x][y];
    }

    return 0;
}

包含两种路径长度

原题链接

题目描述

给定一个长度为 \(n\) 的 \(3\) 跑道道路 ，一个跑道总共包含 \(n + 1\) 个点 ，编号为 \(0\) 到 \(n\) 。一只青蛙从第二条跑道的 \(0\) 号点出发 ，终点为任一跑道的点 \(n\) 处。跑道上可能有一些障碍(保证点\(0\) 和点 \(n\) 处任一跑道均无障碍)。面对前方的障碍时，青蛙可以选择侧跳到其它跑道(两条跑道可以不相邻)的同一点，询问到达终点青蛙最少的侧跳次数

​ 示例：

​ 下图中青蛙的最少侧跳次数为2

​

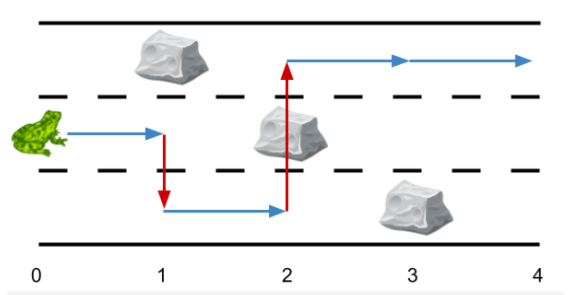
题目分析

将左右移动的花费设为0，上下移动的花费设为1，显然本题可以抽象为边权仅含0和1的图上单源最短路问题。使用最短路算法自然可以解决，但是需要建图。而BFS是无需建图的，可以直接搜索。但BFS的问题在于，其仅能解决边权均相等的图，所以引入双端队列解决这个缺陷。

• 解题策略：

  仍按照一般BFS的搜索顺序，从双端队列队头取点进行扩展。不同的是当遇到边为0的点放入队头，边为1的点放入队尾。所有状态扩展完毕后得到终点的最短路径

• 证明双端队列加持下的BFS的正确性：

  只需证明此时的序列仍然满足两段性和单调性即可。假设此时的序列为 \(|x, x, x, | x+1, x+1, x+1|\)，从队头取出元素\(x\)，若扩展出的点边为0则将\(x+0\)放入队头，边为1则将\(x+1\)放入队尾，显然变化后的序列仍然满足两段性和单调性，即双端队列BFS是正确的。

解题代码(C++)

// leetcode部分实现
const int N = 500010;

class Solution {
public:
    int bfs(vector<vector<int>> &g, int n) 
    {
        vector<vector<bool>> st(3, vector<bool>(N, false));
        vector<vector<int>> dis(3, vector<int>(N, 0x3f3f3f3f));
        
        deque<pair<int, int>> q;
        int dx[] = {-2, -1, 1, 2, 0, 0}, dy[] = {0, 0, 0, 0, 1, -1};

        q.push_front({1, 0});
        dis[1][0] = 0;

        while (q.size())
        {
            auto t = q.front(); q.pop_front();
            int x = t.first, y = t.second;

            if (st[x][y]) continue;
            st[x][y] = true;

            for (int i = 0; i < 6; ++ i) {
                int a = x + dx[i], b = y + dy[i];
                if (a < 0 || a >= 3 || b < 0 || b >= n) continue;
                if (g[a][b] == 1) continue; // 有障碍无法走

                if (dis[a][b] > dis[x][y] + (i == 0 || i == 1 || i == 2 || i == 3))
                {
                    dis[a][b] = dis[x][y] + (i == 0 || i == 1 || i == 2 || i == 3);
                    if (i == 0 || i == 1 || i == 2 || i == 3) q.push_back({a, b});
                    else q.push_front({a, b});
                }
            }
        }

        int res = 0x3f3f3f3f;
        for (int i = 0; i < 3; ++ i)
            res = min(res, dis[i][n - 1]);
        return res;
    }
    int minSideJumps(vector<int>& obstacles) {
        
        vector<vector<int>> g(3, vector<int>(N, 0));
        int n = obstacles.size();

        for (int i = 0; i < n; ++ i) 
            if (obstacles[i]) g[obstacles[i] - 1][i] = 1;
        
        return bfs(g, n);
    }
};

// 全部实现
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <deque>

using namespace std;

const int N = 500010;

int n;
int obstacles[N], g[3][N];
int st[3][N];
int dis[3][N];

int bfs() 
{
    memset(dis, 0x3f, sizeof dis);
    
    deque<pair<int, int>> q;
    int dx[] = {-2, -1, 1, 2, 0, 0}, dy[] = {0, 0, 0, 0, 1, -1};

    q.push_front({1, 0});
    dis[1][0] = 0;

    while (q.size())
    {
        auto t = q.front(); q.pop_front();
        int x = t.first, y = t.second;

        if (st[x][y]) continue;
        st[x][y] = true;

        for (int i = 0; i < 6; ++ i) {
            int a = x + dx[i], b = y + dy[i];
            if (a < 0 || a >= 3 || b < 0 || b >= n) continue;
            if (g[a][b] == 1) continue; // 有障碍无法走

            if (dis[a][b] > dis[x][y] + (i == 0 || i == 1 || i == 2 || i == 3))
            {
                dis[a][b] = dis[x][y] + (i == 0 || i == 1 || i == 2 || i == 3);
                if (i == 0 || i == 1 || i == 2 || i == 3) q.push_back({a, b});
                else q.push_front({a, b});
            }
        }
    }

    int res = 0x3f3f3f3f;
    for (int i = 0; i < 3; ++ i)
        res = min(res, dis[i][n - 1]);
    return res;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; ++ i) cin >> obstacles[i];

    for (int i = 0; i < n; ++ i) 
        if (obstacles[i]) g[obstacles[i] - 1][i] = 1;

    cout << bfs() << endl;

    return 0;
}

最小步数问题

在连通块问题和最短路问题中，搜索的点均为图上的一个有坐标的点。在最小步数问题中，搜索的点变为一个包含各种信息的状态。不过在理解了相关问题之后，可以发现这些状态实际上还是可以看为图上的点。

一般做法

题目描述

原题链接

一个板子含有8个格子，每一个方格都有一种颜色。从板子的左上角开始，沿顺时针方向依次取出整数，构成一个颜色序列。可以用改颜色序列表示这个板子的状态。

例如：可以用序列12345678表示下面这个板子(同时该状态作为基本状态)

1 2 3 4
8 7 6 5

题目提供三种基本操作(由基本状态进行演示)：

• A：交换上下两行

  8 7 6 5
  1 2 3 4
  

• B：将最右边的一列插入到最左边

  4 1 2 3
  5 8 7 6
  

• C：魔板中央对的4个数作顺时针旋转

  1 7 2 4
  8 6 3 5
  

给定目标状态，询问由基本状态到目标状态的操作序列

题目分析

由基本状态到目标状态，每一个状态都是一个颜色序列。搜索的图上的”点”也就变为了这些序列。

两个"点"之间仅通过一步操作，所以图上边权均相等，采用一般BFS即可。

目前的重点在于理解“搜索的点实际上是一个状态”，至于代码实现时所需的哈希，通过坐标变换实现一维空间与二维空间的相互映射这里就不再赘述了

代码实现

/**
 * 坐标映射
 * A:字符串翻转
 * B:a[3]移动到a[0],a[4]移动到a[7]
 * c:a[1]->a[2], a[2]->a[5], a[5]->a[6], a[6]->a[1]
 * 
 * 由于本题只有两行，所以也可以采用二维数组直接模拟二维空间，不需要进行一维到二维的坐标映射
 */
#include <iostream>
#include <algorithm>
#include <string>
#include <map>
#include <unordered_map>

using namespace std;

typedef pair<char, string> PII;

const int N = 40500;

unordered_map<string, int> dis;
unordered_map<string, PII> path;
string q[N];
char stk[N];

int bfs(string end)
{
    string start = "12345678";
    int hh = 0, tt = -1;
    dis[start] = 0;
    q[++ tt] = start;

    while (tt >= hh)
    {
        string t = q[hh ++];
        if (t == end) return dis[t];

        string a(t);
        reverse(a.begin(), a.end());
        if (!dis.count(a)) 
        {
            dis[a] = dis[t] + 1;
            path[a].first = 'A', path[a].second = t;
            q[++ tt] = a;
        }

        string b(t);
        char u(b[3]), v(b[4]);
        for (int i = 3; i > 0; -- i) b[i] = b[i - 1];
        b[0] = u;
        for (int i = 4; i < 7; ++ i) b[i] = b[i + 1];
        b[7] = v;
        if (!dis.count(b))
        {
            dis[b] = dis[t] + 1;
            path[b].first = 'B', path[b].second = t;
            q[++ tt] = b;
        }


        string c(t);
        u = c[6];
        c[6] = c[5];
        c[5] = c[2];
        c[2] = c[1];
        c[1] = u;
        if (!dis.count(c))
        {
            dis[c] = dis[t] + 1;
            path[c].first = 'C', path[c].second = t;
            q[++ tt] = c;
        }
    }

    return -1;
}
int main()
{
    string end("");

    for (int i = 0; i < 8; ++ i) 
    {
        char c;
        cin >> c;
        end += c;
    }

    cout << bfs(end) << endl;

    int tt = -1;
    for (string s = end; s != "12345678"; s = path[s].second) stk[++ tt] = path[s].first;
    while (tt >= 0) cout << stk[tt --];

    return 0;
}

优化-双向BFS

首先考虑 \(a^b\) 与 \(2 × a^{\frac{b}{2}}\) 的大小关系。

\(\frac{a^b}{2 × a^{\frac{b}{2}}} = \frac{a^{\frac{b}{2}}}{2}\), 即两者的大小关系取决于 \(\frac{b}{2}\) 和 \(2\) 的大小关系

现实问题中绝大多数情况是\(\frac{b}{2} > 2\)，即 \(a^b > 2 × a^{\frac{b}{2}}\)

\(a^b > 2 × a^{\frac{b}{2}}\) 就清晰地阐述了一般BFS同双向BFS的关系。一般BFS采用的单向搜索，状态数量的增加并非是线性级别的，而是指数级别的，就类似下图这样，搜到终点时，开口已经非常大了，这就意味着无效搜索非常多。

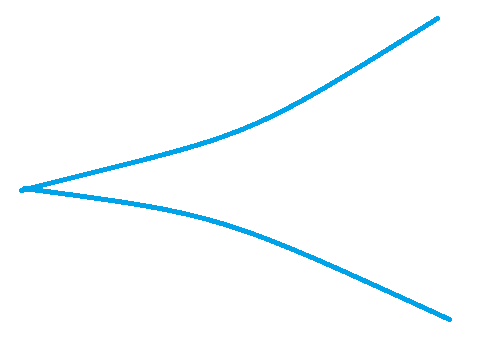
双向BFS是指从起点和终点同时向中间搜索(注意这里说的同时并非指同步)，对于每一部分，都可以避免随指数级别增加的状态数量的大幅增加，从而加快搜索速度。

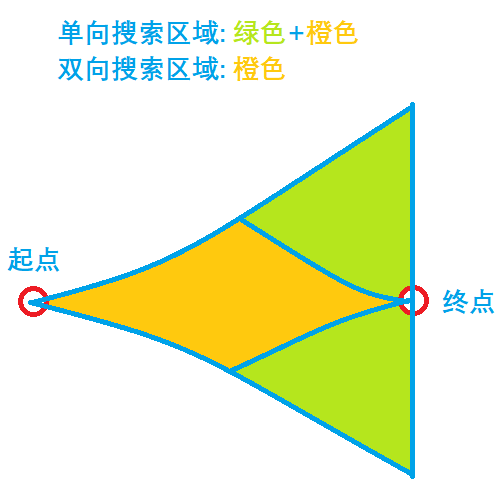
题目描述

给定两个字符串A, B和一组字符串变换的规则,询问从A变换到B最少需要几次变换

字符串变换规则abc->xu指: 字符串中的abc可以替换为xu

题目分析

如果按照单向搜索的一般BFS来做，本题和一般做法中所提及的题目解法思路完全相同。

如果按照双向BFS来做，搜索方向应在起点到终点和终点到起点二者中选择当前搜索队列中数量较少的，以减少搜索的状态数量，其余过程与单向搜索相同

解题代码(C++)

单向BFS：

/**
 * 搜索的思路并不难想到，每一个状态都是一个字符串
 * 向外拓展就是使用每一个规则进行替换
 * 难点在于如何使用每一个规则
 * 
 * 看完讲解发现是自己想复杂了，规则的使用就是字符串的一般处理，不会涉及到什么复杂的字符串算法，觉得复杂完全是畏惧心里，就像此前面对树和图的问题一样
 * 
 * 本题的核心考点显然不是变换规则如何使用。由于状态数量过多，一般的bfs会超时，应当从起点和终点同时向中间搜索，
 * 如果是单向搜索，状态数量的增加并不是线性级别的，而是指数级别的，单向搜索与从两端向中间搜索的差别类似a^b与2*a^(b/2)的差别
 * 会大幅度减少搜索的状态数量，为了更加清晰的理解，首先实现一下单向bfs
 * 
 * 写完代码真的发现，感觉字符串问题较难不是我的错觉，是真的和其它问题不一样，在一些问题上很容易就想错或想不明白
 */
 
// 单向bfs
#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>

using namespace std;

const int N = 10;

int n;
string A, B;
string a[N], b[N];
queue<string> q;
unordered_map<string, int> dis;

/**
 * 第一次写遇到一个问题是在用a替换为b时只替换了第一个a就直接返回了
 * 写之前确实想到了这个问题，如果有多个匹配的a怎么办
 * 实际是当前只替换1个，放进队列后再遇到这个自然就会继续替换，替换1个，2个，。。。的情况都可以搜索到
 * 但是如果有多个位置匹配，虽然说只替换一个，但是要将替换每一个位置的情况全部放进队列，而非第一个匹配的位置
 */
void extend(string t, string a, string b) // 把t中a的部分换为b
{
    for (int i = 0; i < t.size(); ++ i)
        if (t.substr(i, a.size()) == a)
        {
            string ex = t.substr(0, i) + b + t.substr(i + a.size());
            
            if (dis.count(ex)) continue;
            
            q.push(ex);
            dis[ex] = dis[t] + 1;
        }
}
int bfs()
{
    q.push(A);
    dis[A] = 0;
    
    while (q.size())
    {
        string t = q.front();
        q.pop();
        
        if (t == B) return dis[t];
        
        for (int i = 0; i < n; ++ i)
            extend(t, a[i], b[i]); 
    }
    
    return 11;
}
int main()
{
    cin >> A >> B;
    
    while (cin >> a[n] >> b[n]) ++ n;
    
    int t = bfs();
    
    if (t > 10) cout << "NO ANSWER!" << endl;
    else cout << t << endl;
    
    return 0;
}

双向BFS：

/**
 * 双向bfs作为bfs的优化
 * 主要应用于最小步数模型中，即待搜索状态数极大的问题中
 * 棋盘中的路径问题不需要使用双向bfs是因为格点数目不会很大，搜索耗时较少
 * 
 * 双向bfs就是从起点和终点同时向中间搜索，从数学角度来看能够大幅度减少搜索的状态数量
 * 每次从元素数量较少的队列中取元素
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstring>
#include <queue>
#include <unordered_map>

using namespace std;

const int N = 10;

int n;
string A, B;
string a[N], b[N];
queue<string> qa, qb;
unordered_map<string, int> da, db;

/**
 * 考虑q队列，里面元素的距离为da，另一队列中元素距离为db，将其中的a替换为b
 * 这里必须要加上da，db，否则我们不知道q队列的元素t的距离到底是da[t]还是db[t]
 */
int extend(queue<string> &q, unordered_map<string, int> &da, unordered_map<string, int> &db, string a[], string b[])
{
    // 我们要做的是将当前q中的元素全部拓展一遍，但是这样写会将拓展后的点也会被遍历
    // while (q.size())
    for (int k = 0, qs = q.size(); k < qs; ++ k)
    {
        string t = q.front();
        q.pop();
        
        for (int i = 0; i < t.size(); ++ i)
            for (int j = 0; j < n; ++ j)
                if (t.substr(i, a[j].size()) == a[j])
                {
                    string state = t.substr(0, i) + b[j] + t.substr(i + a[j].size());
                    
                    if (da.count(state)) continue;
                    if (db.count(state)) return da[t] + 1 + db[state] ; // 已经找到交点就可以返回距离了, da[t] + 1就是da[state]，因为此时da[state]还没有更新所以用da[t]
                    
                    da[state] = da[t] + 1;
                    q.push(state);
                }
    }
    
    return 11; // q在拓展时并没有找到交点
}
int bfs()
{
    qa.push(A); da[A] = 0;
    qb.push(B); db[B] = 0;
    
    /**
     * 有解的条件是从起点向终点走和从终点向起点走应该能够走到同一个状态
     * 如果某个方向已经走完了还没有相遇就说明无解
     * 上面这个结论为什么是正确的？
     * 为了叙述的方便，我们定义从起点向终点走为方向a，从终点向起点走为方向b，
     * 我考虑一种情况为若b已经把所有情况都搜索完了，a还没有搜索完，此时还没遇到交点(交点就是a和b都走过的某个状态，显然起点和终点都算是交点)，会不会可能交点在b中，但是a还没有走到交点
     * 这种想法是错误的，原因在于如果问题是有解的，那么单从b方向而言，最终一定是可以到达起点的
     * 就算是a方向上完全没有动，单从b方向也一定是可以走到起点的，这就变为了单向bfs
     * 而b的所有情况都搜索完成后并没有找到交点(这其中可是包含起点的)，说明起点与终点之间是不存在通路的，即无解
     * 
     * 所以bfs的条件是两个队列均不为空，在这期间如果找到了答案说明有解，某个队列已经空了还没找到答案说明无解
     */
    while (qa.size() && qb.size())
    {
        int t;
        if (qa.size() <= qb.size()) t = extend(qa, da, db, a, b); // 对于qa 将a替换为b
        else t = extend(qb, db, da, b, a);
        
        if (t <= 10) return t;
    }
    
    return 11;
}
int main()
{
    cin >> A >> B;
    
    while (cin >> a[n] >> b[n]) ++ n;
    
    int t = bfs();
    
    if (t > 10) cout << "NO ANSWER!" << endl;
    else cout << t << endl;
    
    return 0;
}

优化-A*

如何理解A*

A*作为一种优化，必然是针对一般BFS的某个缺点而产生的。在最小步数问题中，搜索空间可能非常大，以至于使用双向BFS仍然会超时。这是因为双向BFS的优化只是从数学维度降低了搜索空间的大小，搜索逻辑和一般BFS相比并没有发生改变，它们采用的逻辑均为首先搜索距离起点较近的状态，但这些状态到终点的距离可能很大，综合来看它们并非最终答案。优先搜索这些状态浪费了大量时间，A*就是将这种仅考察局部因素的搜索策略改为考察全局因素，不仅参考前段路长度还参考后段路径长度，即优先搜索那些距离起点路径长度+距离终点距离长度更小的状态，这些状态显然更容易到达终点。

• 从代码实现上来看，A*将一般BFS采用的队列更改为优先队列。队列只有在路径长度均相等的情况下才可以保证序列的两段性和单调性，即保证搜索的正确性。但距离起点路径长度+距离终点距离长度显然不会全部相等，同时搜索是具备优先级的，所以需要使用优先队列
• 从逻辑上来看，A*引入了一个估价函数，从而改变了BFS的搜索顺序。从起点a走到状态b，b距离a的距离是已知的，但到达终点的距离是未知的，但是我们需要使用这个值来判断搜索的优先级，所以引入了估价函数作为某个状态到达终点的预估距离。预估距离并不会计算到答案上，它只是改变了搜索的顺序

估价函数

从上述分析中可以得知，A*的关键在于找到估价函数。估价函数的选取有以下两点规则和性质

1. 估价值与真实值偏差越小，优化效果越好

   这并不难理解，当估价值\(==\)真实值时，搜索路径就是最佳路径，直接走到终点

2. \(估价值≤真实值\)

   考虑有两个状态\(a\)和\(b\)，从\(a\)和\(b\)均可以到达终点，\(两者的估价值均分别>其自身真实值\)，并有\(估价值a>估价值b\)，\(真实值a<真实值b\)，根据估价值，首先搜索状态b，并搜索到终点，搜索过程结束。显然得到的结果是错误的，从状态a到达终点可以获取到更短距离，但由于\(a的估价值>b的估价值\)，所以选择了错误的搜索顺序。所以保证\(估价值≤真实值\)的意义在于当\(a的真实值<b的真实值\)时，可以保证\(a的估价值<b的估价值\)；当\(a的真实值>b的真实值\)时，即\(b的真实值<a的真实值\)时，保证\(b的估价值<a的估价值\)，无论在以上哪种情况下， 都可以保证根据估价值的大小选择的搜索路径一定是正确的。

需要注意的是在\(2\)的讨论中，根据真实值的大小关系可以得到估价值的大小关系，但反之是不成立的。在上述证明中，我们考虑了\(a的真实值<b的真实值\)和\(a的真实值>b的真实值\)两种情况，这两种情况已经包含了所有可能，并且在\(估价值≤真实值\)的条件下，可以确定这两种情况均可得到正确答案，所以证明是正确的。但实际执行过程是根据估价值的大小关系确定搜索的先后顺序，但是估价值小的状态真实值可能更大，但最终仍可得到正确答案，考虑两个状态a和b，满足\(估价值a<估价值b\)，\(真实值a>真实值b\)，从a开始搜索，虽然走了错误的路径，但在终点未出队之前某个状态c(该状态可能是终点，当a和b与终点直接相连时，这里的状态就是指终点)的估价值一定会>b的估价值(\(估价值≤真实值\)，\(真实值b<真实值c\)，所以可得\(估价值b<估价值c\))，所以一定会从b再走一次以完成修正的过程。

需要关注的问题

A*只有在保证有解时具有较高的搜索效率，无解时甚至不如一般BFS效率高。这是由于，在无解时A*与一般BFS一样要搜索完搜索可搜索状态，但BFS采用的是队列，读写均为\(O(1)\)，但是A*采用优先队列，堆中的写操作是\(O(logn)\)的，所以效率反而会更差一些。这就解释了在下面的A*代码中为何要首先判断是否有解才开始进行搜索。

当然在实际问题中很难在解决问题之前就判断出是否有解，采用A*也只能是一般做法无法解决，抱着一种试试看的态度

题目描述

在一个 \(3×3\) 的网格中，\(1∼8\) 这 \(8\) 个数字和一个 X 恰好不重不漏地分布在这 \(3×3\) 的网格中。

例如：

1 2 3
X 4 6
7 5 8

可以把 X 与其上、下、左、右四个方向之一的数字交换（如果存在）

目的是通过交换，使得网格变为如下排列（称为正确排列）：

1 2 3
4 5 6
7 8 X

把 X 与上下左右方向数字交换的行动记录为 u、d、l、r

给你一个初始网格，询问最少通过几次移动可以得到正确排列，若存在解决方案，则输出得到正确排列的完整行动记录，如果答案不唯一，输出任意一种合法方案。如果不存在解决方案，则输出 unsolvable

题目分析

为何采用A*而非一般BFS在上述A*的介绍中已经提到，这里不再赘述，直接考虑A*的实现方式。

关键在于确定估价函数以保证\(估价值≤真实值\).对于一个状态，变换为正确排列需要把每个数移动到正确位置，仅对一个数而言，移动到目标位置最少的移动次数是当前位置距离目标位置的曼哈顿距离，所以我们考虑将所有数距离各自目标位置的曼哈顿距离求和作为估价值，一定能够保证\(估价值≤真实值\)，因为仅对一个数而言最少移动次数是曼哈顿距离，但多个数同时考虑可能需要一些额外操作，\(真实值是\geq曼哈顿距离和\)的。

对于八数码问题，一定有解的充要条件为将二维数组按照行优先的顺序从左到右依次读取获得的序列的逆序对数量一定为偶数

• 必要性证明(问题有解说明逆序对数量一定为偶数)：因为行内移动不会改变逆序对，行间移动对于逆序对数量的改变为偶数，所以任何变换都不会改变序列逆序对数量的奇偶，目标序列的逆序对数量为0，即偶数，所以只有当初始状态序列的逆序对数量为偶数时才有可能化为目标状态

• 充分性证明(初始逆序对数量为偶数则问题一定有解)：较难证明

解题代码(C++)

一般BFS:

#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>

using namespace std;

string bfs(string start)
{
    string end = "12345678x";
    queue<string> q;
    unordered_map<string, int> dis;
    unordered_map<string, pair<string, char>> prev;
    char op[] = {'u', 'r', 'd', 'l'};
    int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
    
    q.push(start);
    dis[start] = 0;
    
    while (q.size())
    {
        string t = q.front(); q.pop();
        int k = t.find('x');
        int x = k / 3, y = k % 3;
        
        if (t == end)
        {
            string res("");
            while (end != start)
            {
                res += prev[end].second;
                end = prev[end].first;
            }
            reverse(res.begin(), res.end());
            return res;
        }
        for (int i = 0; i < 4; ++ i)
        {
            int a = x + dx[i], b = y + dy[i];
            string str(t);
            swap(str[k], str[a * 3 + b]);
            string state =str;
            
            if (a < 0 || a >= 3 || b < 0 || b >= 3) continue;
            if (dis.count(state)) continue;
            
            dis[state] = dis[t] + 1;
            prev[state] = {t, op[i]};
            q.push(state);
        }
    }
    
    return "unsolvable";
}
int main()
{
    string start("");
    
    char c;
    while (cin >> c) start += c;
    
    string t = bfs(start);
    
    cout << t << endl;
    
    return 0;
}

A*优化

#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>

using namespace std;

int f(string state) // 估价函数-获取状态state的估价值
{
    int res = 0;
    for (int i = 0; i < state.size(); ++ i)
        if (state[i] != 'x')
        {
            int t = state[i] - '1';
            res += abs(i / 3 - t / 3) + abs(i % 3 - t % 3);        
        }
    return res;
}
string bfs(string start)
{
    string end = "12345678x";
    char op[] = {'u', 'r', 'd', 'l'};
    int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
    
    unordered_map<string, int> dis;
    unordered_map<string, pair<string, char>> prev;
    priority_queue<pair<int, string>, vector<pair<int, string>>, greater<pair<int, string>>> heap;
    
    dis[start] = 0;
    heap.push({f(start), start});
    
    while (heap.size())
    {
        auto t = heap.top(); heap.pop();
        string state = t.second;
        int k = state.find('x');
        int x = k / 3, y = k % 3;
        
        if (state == end)  break;
        for (int i = 0; i < 4; ++ i)
        {
            int a = x + dx[i], b = y + dy[i];
            if (a < 0 || a >= 3 || b < 0 || b >= 3) continue;
            
            string tmp(state);
            swap(tmp[k], tmp[a * 3 + b]);
            
            if (!dis.count(tmp) || dis[tmp] > dis[state] + 1) // 此前除了dijkstra都是直接更新dis[tmp]，不需要判断，而dijkstra实现时用的是数组都进行了初始化，这里并没有初始化，虽然默认值是0但从严谨性的角度来说还是要判断是否是不存在的情况的
            {
                dis[tmp] = dis[state] + 1;
                prev[tmp] = {state, op[i]};
                heap.push({dis[tmp] + f(tmp), tmp}); // 注意我们存放的应该是起点到该状态距离+该状态到终点的预估距离，即考虑的是最终答案，按照最终答案的大小安排的搜索顺序才是最优的
            }
        }
    }
    
    string res("");
    while (end != start)
    {
        res += prev[end].second;
        end = prev[end].first;
    }
    reverse(res.begin(), res.end()); // 记得翻转
    return res;
}
int main()
{
    char c;
    string start, seq;
    
    while (cin >> c)
    {
        start += c;
        if (c != 'x') seq += c;
    }
    
    int cnt = 0;
    for (int i = 0; i < seq.size(); ++ i)
        for (int j = i + 1; j < seq.size(); ++ j)
            if (seq[i] > seq[j]) ++ cnt;
    
    if (cnt & 1) cout << "unsolvable" << endl;
    else cout << bfs(start) << endl;
    
    return 0;
}

多源BFS

题目描述

给定一个 \(N\) 行 \(M\) 列的 \(01\) 矩阵 \(A\)，\(A[i][j]\) 与 \(A[k][l]\) 之间的曼哈顿距离定义为：

\(dist(A[i][j],A[k][l])=|i−k|+|j−l|\)

输出一个 \(N\) 行 \(M\) 列的整数矩阵 \(B\)，其中：

\(B[i][j]=min_{1≤x≤N,1≤y≤M,A[x][y]=1}dist(A[i][j],A[x][y])\)

题目分析

题目通俗地讲就是求矩阵中所有0距离1的最小曼哈顿距离

正向思路是遍历矩阵,从所有0开始BFS求距离1的最短距离,结果没有错误但是会TLE

俗话说"正向求解困难就尝试反向求解"

反向思路显然是从所有1开始BFS,过程中更新各个0的答案,这样做的正确性证明是比较难想的.很巧妙地是引入一个虚拟源点的概念,该点距离所有1的距离均为0.对所有0而言,距离1的最近距离即为距离虚拟源点的最近距离.所以问题已经转变为从虚拟源点开始的单源最短路问题,即Dijkstra.Dijkstra是正确的,所以显然该做法也是正确的.

解题代码(C++)

正向求解:

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

typedef pair<int, int> PII;

const int N = 1010, M = N * N;

int n, m;
int g[N][N];
char ch[N][N];
PII q[M];
bool st[N][N];
int dis[N][N], step;

void bfs(int sx, int sy)
{
    int hh = 0, tt = -1;
    int dx[] = {-1, 0, 1, 0};
    int dy[] = {0, 1, 0, -1};
    
    memset(st, 0, sizeof st);
    st[sx][sy] = true;
    q[++ tt] = {sx, sy};
    step = 0;
    
    while (tt >= hh)
    {
        int size = tt - hh + 1;
        while (size --)
        {
            PII t = q[hh ++];
            int a = t.first, b = t.second;
            
            if (g[a][b]) 
            {
                dis[sx][sy] = step;
                return ;
            }
            for (int i = 0; i < 4; ++ i)
            {
                int x = a + dx[i], y = b + dy[i];
                if (x < 0 || x >= n || y < 0 || y >= m || st[x][y]) continue;
                
                st[x][y] = true;
                q[++ tt] = {x, y};
            }
        }
        ++ step;
    }
}
int main()
{
    cin >> n >> m;
    
    for (int i = 0; i < n; ++ i) cin >> ch[i];
    
    for (int i = 0; i < n; ++ i)
        for (int j = 0; j < m; ++ j)
            g[i][j] = ch[i][j] - '0';
    
    for (int i = 0; i < n; ++ i)
        for (int j = 0; j < m; ++ j)
            if (!g[i][j]) bfs(i, j);
            
    for (int i = 0; i < n; ++ i)
    {
        for (int j = 0; j < m; ++ j)
            cout << dis[i][j] << ' ';
        cout << endl;
    }
     
    return 0;       
}

反向求解:

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

typedef pair<int, int> PII;

const int N = 1010, M = N * N;

int n, m;
char g[N][N];
int dis[N][N];
PII q[M];

void bfs()
{
    int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
    int hh = 0, tt = -1;
    memset(dis, -1, sizeof dis);
    
    for (int i = 0; i < n; ++ i)
        for (int j = 0; j < m; ++ j)
            if (g[i][j] == '1')
            {
                dis[i][j] = 0;
                q[++ tt] = {i, j};
            }
    
    while (tt >= hh)
    {
        PII t = q[hh ++];
        int a = t.first, b = t.second;
        
        for (int i = 0; i < 4; ++ i)
        {
            int x = a + dx[i], y = b + dy[i];
            if (x < 0 || x >= n || y < 0 || y >= m || dis[x][y] != -1) continue;
            
            dis[x][y] = dis[a][b] + 1;
            q[++ tt] = {x, y};
        }
    }
    
}
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; ++ i) cin >> g[i];
    
    bfs();
    
    for (int i = 0; i < n; ++ i)
    {
        for (int j = 0; j < m; ++ j) cout << dis[i][j] << ' ';
        cout << endl;
    }
    
    return 0;
}

区别与联系

这里主要讨论Dijkstra，一般BFS，双端队列BFS和A*之间的区别和联系

联系
无论使用哪种解决方法，本质上解决的都是单源最短路问题，所以本质上均为Dijkstra的思想

区别

算法	特征
Dijkstra(堆优化版)	入队多次，每个点第一次出队时即为最短路径
一般BFS	入队一次，每个点第一次出队时即为最短路径
双端队列BFS	入队多次，每个点第一次出队时即为最短路径
A*	入队多次，除终点外其余点出队时均不一定为最短路径，终点第一次出队即为最短路径

虽然本质上均采用的Dijkstra算法思想，但是由于条件的不同实际的执行过程也不相同，接下来对一般BFS，双端队列BFS和A*进行分别论述

某个点可以被放入对队列说明该点的距离值得到更新

• 一般BFS

  入队一次的原因在于路径长度唯一(假设为1)，队列中有两个点a和b，两者到c点的距离均为1，若\(d_a == d_b\),显然\(d_a + 1 = d_b + 1\)，由于扩展出的距离相等，所以c点仅需入队一次，若\(d_a < d_b\)，显然\(d_a + 1 < d_b + 1\)，第一次入队后第二次距离不需要更新所以仍是仅入队一次。

  在最短路问题中已经证明了每个点出队时对应的路径即为最短路径，这里不再赘述

• 双端队列BFS

  入队多次的原因在于路径长度不唯一(假设为0和1)，队列中有两个点\(d_a == d_b\)，两种到c点的距离分别为1和0，显然\(d_a + 1 > d_b + 0\)，所以c点就会两次入队。

  与一般BFS一样具有两段性和单调性，所以可证明得到每个点第一次出队时即为最短路径(证明方法与一般BFS相同)

• A*

  入队多次的原因在于路径长度不唯一

  由于我们搜索顺序的依据始终是距离终点的预估距离，优先搜索的是距离终点预估距离小的点，而预估距离是考虑的是全段而非仅仅是距离起点的距离，所以只能保证终点出对时得到最短距离，其余点均无法得到保证